필요한 사전지식
- 이진트리(특히, 균형잡힌 이진트리)
- LinkedList<> 자료구조
인덱스(Index)
- 인덱스는 데이터를 빠르게 찾을 수 있는 하나의 장치이다.
- 보통 DB에서 사용하는 인덱스는 B-트리 자료구조로 이루어져 있다.
- 루트노드, 리프노드, 그리고 브랜치 노드로 나뉜다.
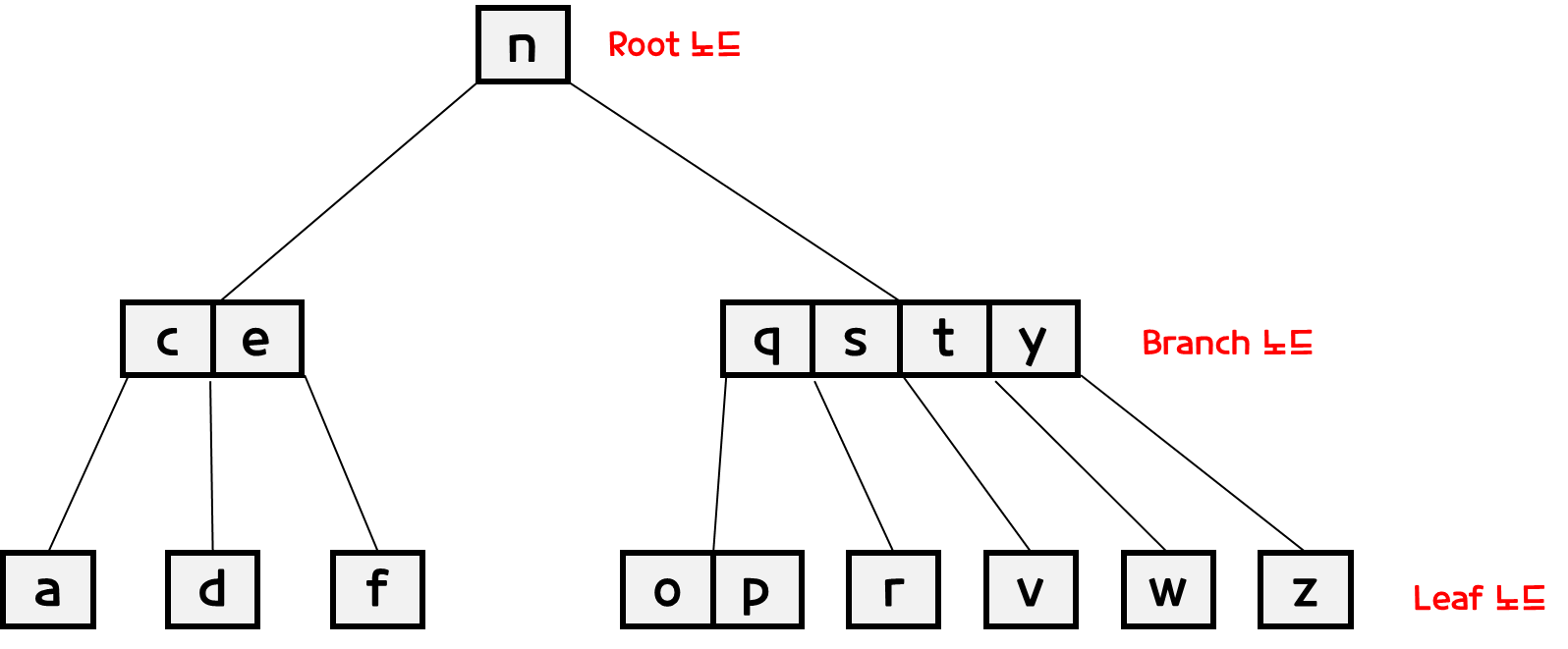
- 루트노드, 리프노드, 그리고 브랜치 노드로 나뉜다.
B-트리
- 대표적인 BalancedTree 중에 하나이다.
- BalancedTree의 목적은 좌우 자식의 밸런스를 맞춰 최대한 높이를 줄여 시간복잡도가 O(logN)이 나오게 만드는 개념이다.
- 하나의 노드에 여러 자료가 배치되는 트리구조이다.
- 한 노드에 최대 M개의 자식 노드을 가질수 있는 B트리를 M차 B-Tree라고 한다.
-
M이 짝수냐/홀수냐에 따라 알고리즘이 많이 상이하다.
-
특히, 짝수 B트리의 경우 어렵다.
-
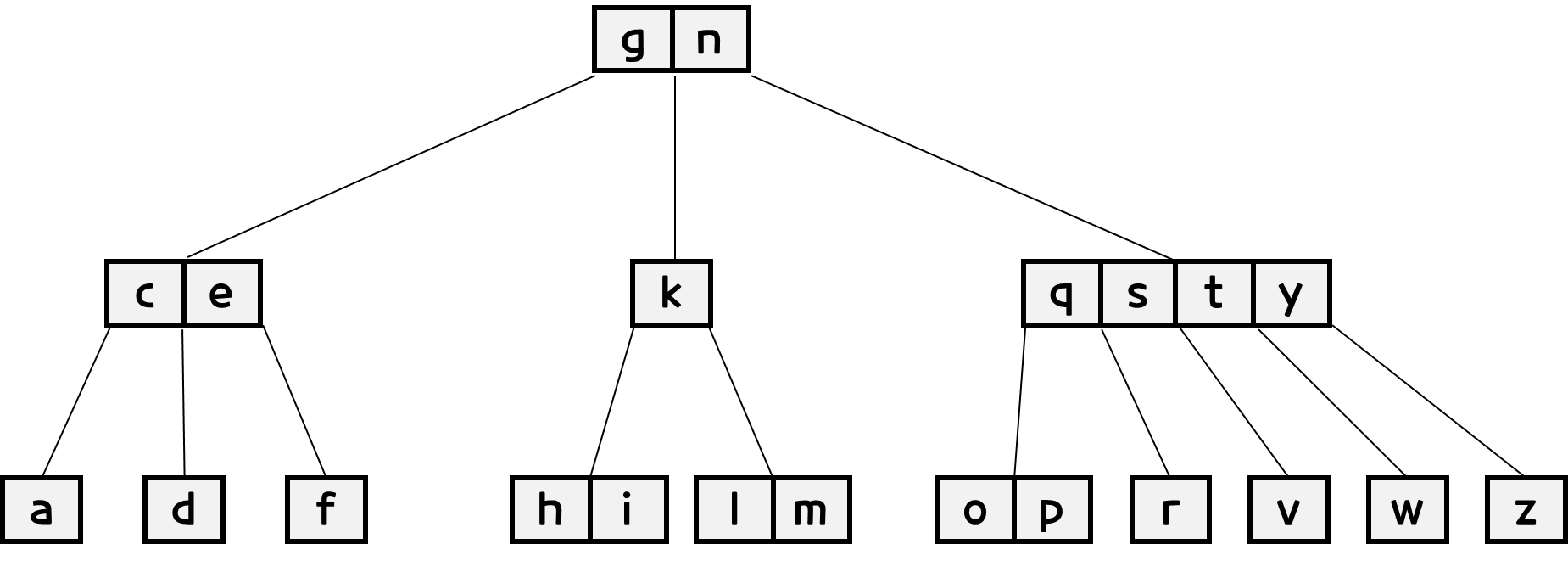
아래 그림은 최대 5개의 자식노드를 가지고 있음으로 5차 B-Tree이다.
-
B-Tree 규칙1
- 노드의 자료수가 N이라면, 자식의 수는 N+1 이어야한다.
- 위 그림처럼, 오른쪽
ekiq노드가 4개의 데이터를 가지고 있어, 자식수는 5개 이어야 한다.
- 위 그림처럼, 오른쪽
- 각 노드의 자료는 정렬된 상태여야 한다.
- 각 노드가 가지고 있는 자료수 만큼 정렬이 되어 있어야 한다.
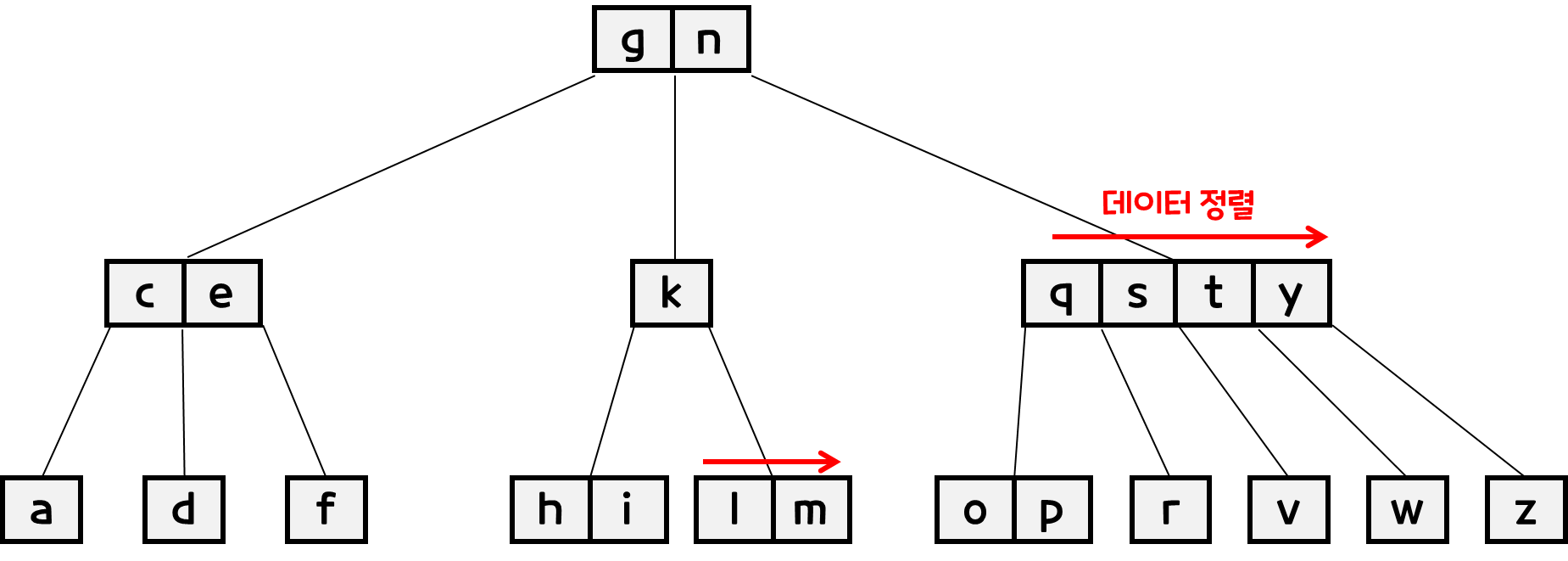
- 각 노드가 가지고 있는 자료수 만큼 정렬이 되어 있어야 한다.
- 가장 중요한 규칙 자료의 노드의 왼쪽 서브트리는 항상 부모 노드 데이터 보다 작아야하고, 오른쪽 서브트리는 항상 커야한다.
- ex)
ce노드의 경우 ,c의 왼쪽 트리는a로 항상 작아야하고, 오른쪽 트리는d,f로 항상 큰 값이다. e의 경우도 왼쪽은a,d오른쪽은f로 되어 있다.
- ex)
B-Tree 규칙2
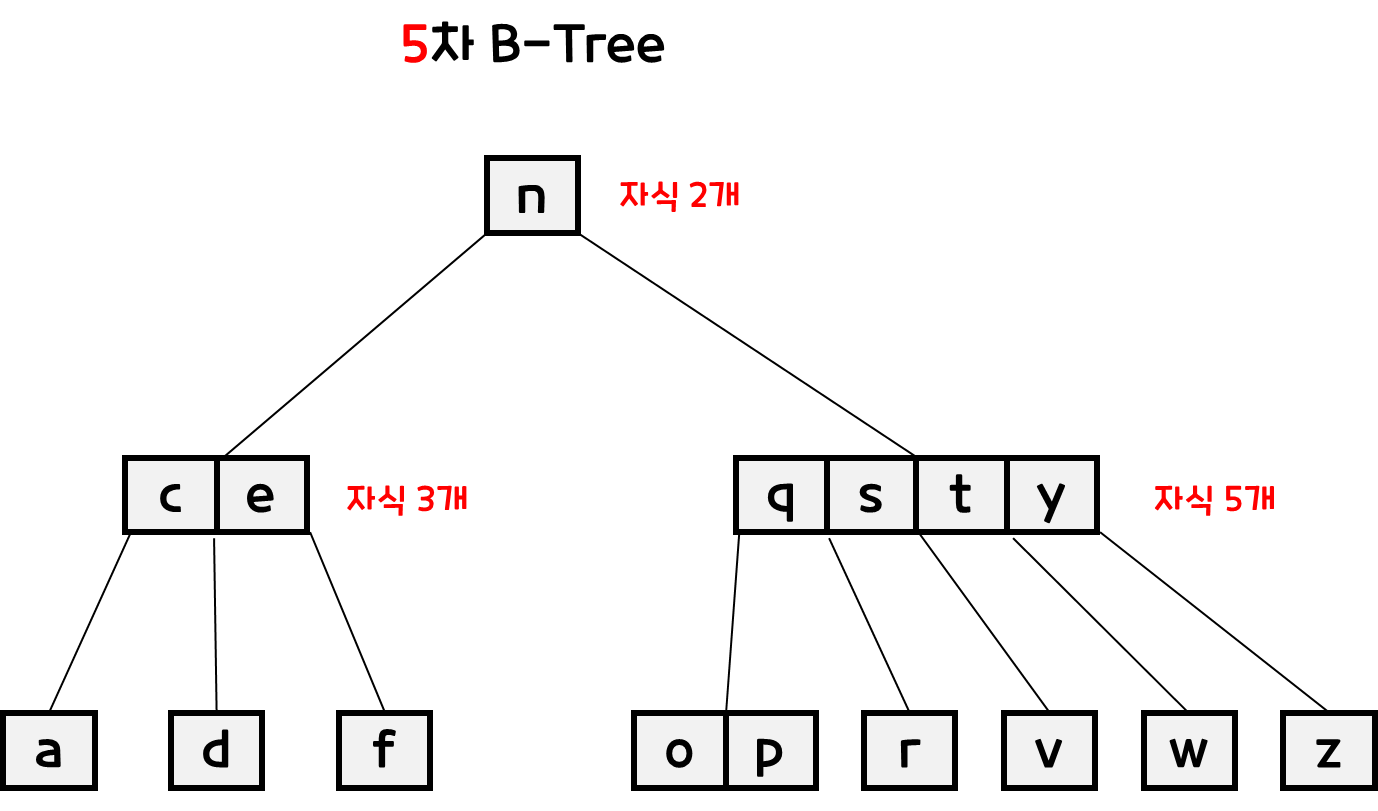
- Root 노드는 적어도 2개이상의 자식을 가져야 된다.
- Root노드를 제외한 모든 노드는 적어도 M/2개의 자료를 가지고 있어야 한다.
- ex. 5차 B-Tree이기 때문에, 2개이상의 자료를 가지고 있어야한다. (1개는 안됨)
- 입력자료는 중복될 수 없다.
- 외부노드로 가는 경로의 길이는 모두 같다. (밸런스 트리)
B-Tree 정리
- 균일한 트리이고, 해당 형태를 유지하기때문에 주요 특징으로 '어떤 값에 대해서도 같은 시간에 결과를 얻을 수 있다'인데, 이를 '균일성'이라고 한다.
- 시간복잡도가 최악,최상 거의 동일하다.
참고자료
인덱스가 효율적인 이유
- 이렇게 B-Tree 형태로 구현되어 있기때문에, 어떤 값을 찾더라도 시간복잡도
O(logN)가 균일하고 빠르게 찾을 수 있다. - 기본적으로 인덱스가 한 깊이씩 증가할 때마다 인덱스 항목의 수는 최대 4배씩 증가한다.
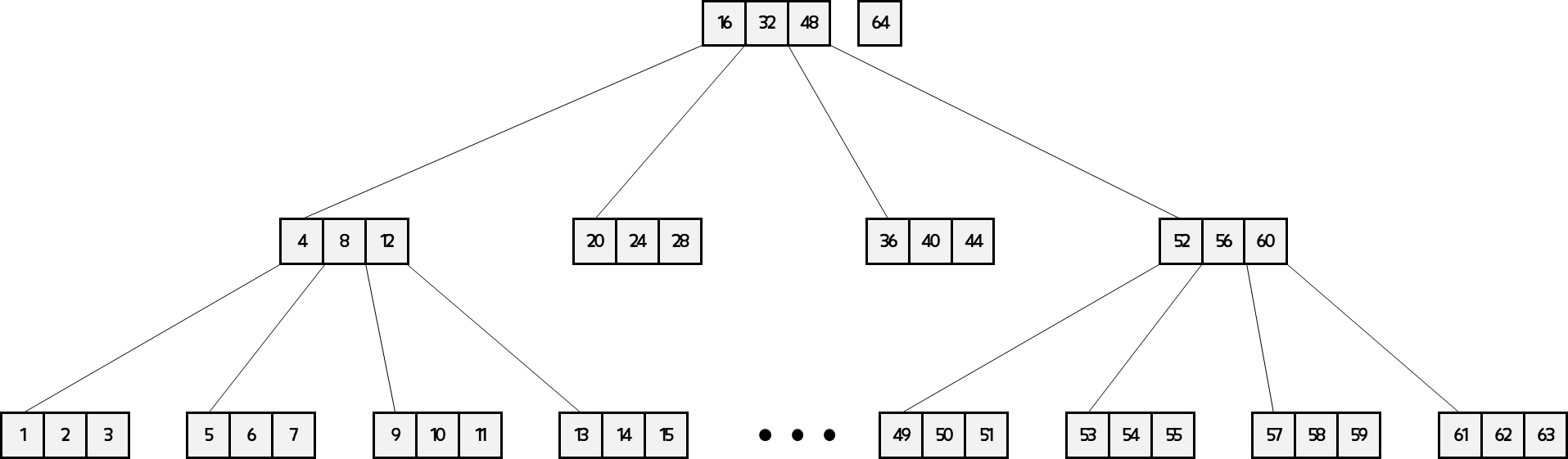
- 인덱스의 깊이를 10까지만 늘려도, 100만개의 레코드를 검색할 수 있게된다.
- 이것을 트리의 대수 확장성이라 부른다.
B-Tree의 한계
- 하지만, B-Tree도 처음 생성할때는 균형한 트리로 생성할 수 있지만, 테이블 갱신(INSERT , UPDATE, DELETE) 의 반복을 통해, 점점 균형이 깨질 것이다.
- 물론 어느정도 자동으로 균형을 유지하려고 하겠지만, 갱신이 잦으면 쉽지않고, 성능도 악화될 것이다.
⇒ 그래서 갱신 빈도가 높은 테이블에는 인덱스를 재구성하여 트리의 균형을 되찾을 필요가 있다.
B+Tree
- B-tree의 확장개념으로, MySQL의 DB 엔진인 InnoDB는 B+Tree 구조로 되어있다.
- B-tree의 경우 internal 또는 branch 노드에 key와 data를 담을 수 있다
- B+tree의 경우 브랜치 노드에 key만 담아두고, data는 담지 않는다.
-
오직 리프노드에만 Key와 data를 저장하고, 리프노드끼리 Linked List로 연결되어 있다.
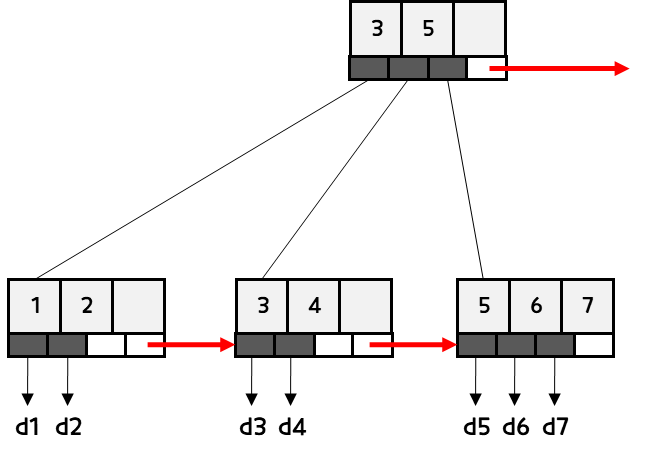
-
B+Tree의 장점
- 리프노드에만 데이터를 담아둠으로써, 나머지(브랜치노드, 루트노드)의 메모리를 더 확보함으로써 더 많은 key들을 수용할 수 있다.
- 한 노드당 Key를 많이 담을 수 있어 트리의 높이가 낮아진다.
- 풀 스캔시, B+Tree는 리프 노드에서 선형 탐색을 진행하여, B-Tree에 비해 빠르다.
- 일반 검색은 B-Tree 구조가 더 빠름
- 루트노드/브랜치노드에도 데이터가 존재하기때문
