데이터 불러오기
보스턴 주택 가격 예측에 대한 데이터셋은 sklearn에서 자체적으로 제공했었지만, 데이터셋 자체의 윤리적 문제로 인해 삭제되었다. 현재는 OpenML에서 제공하고 있다.
import pandas as pd
from sklearn import datasets
x, y = datasets.fetch_openml('boston', return_X_y=True)
x| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3 | 222.0 | 18.7 | 396.90 | 5.33 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 501 | 0.06263 | 0.0 | 11.93 | 0 | 0.573 | 6.593 | 69.1 | 2.4786 | 1 | 273.0 | 21.0 | 391.99 | 9.67 |
| 502 | 0.04527 | 0.0 | 11.93 | 0 | 0.573 | 6.120 | 76.7 | 2.2875 | 1 | 273.0 | 21.0 | 396.90 | 9.08 |
| 503 | 0.06076 | 0.0 | 11.93 | 0 | 0.573 | 6.976 | 91.0 | 2.1675 | 1 | 273.0 | 21.0 | 396.90 | 5.64 |
| 504 | 0.10959 | 0.0 | 11.93 | 0 | 0.573 | 6.794 | 89.3 | 2.3889 | 1 | 273.0 | 21.0 | 393.45 | 6.48 |
| 505 | 0.04741 | 0.0 | 11.93 | 0 | 0.573 | 6.030 | 80.8 | 2.5050 | 1 | 273.0 | 21.0 | 396.90 | 7.88 |
506 rows × 13 columns
데이터 분석
x.columns
Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
'PTRATIO', 'B', 'LSTAT'],
dtype='object')
feature살펴보기
CRIM: 자치시(town) 별 1인당 범죄율ZN: 25,000 평방피트를 초과하는 거주지역의 비율INDUS: 비소매상업지역이 점유하고 있는 토지의 비율CHAS: 찰스강에 대한 더미 변수(강의 경계에 위치한 경우는1, 아니면 0)NOX: 10ppm당 농축 일산화질소RM: 주택 1가구당 평균 방의 개수AGE: 1940년 이전에 건축된 소유주택의 비율DIS: 5개의 보스턴 직업센터까지의 접근성 지수RAD: 방사형 도로까지의 접근성 지수TAX: 10,000달러 당 재산세율PRRATIO: 자치시(town)별 학생/교사 비율B: 1000(Bk-0.63)^2, 여기서 Bk는 자치시별 흑인의 비율LSTAT: 모집단의 하위계층의 비율(%)MEDV: 본인 소유의 주택가격(중앙값) (단위: $1,000)
feature목록을 보면 거의 모든 feature가 예측값에 영향을 줄 수 있는 데이터라고 판단할 수 있다. 하지만 윤리적 문제로 인해 B는 삭제하고 진행하도록 하겠다.
데이터 결측치 확인
x = x.drop(['B'], axis=1)
x.isnull().sum()CRIM 0
ZN 0
INDUS 0
CHAS 0
NOX 0
RM 0
AGE 0
DIS 0
RAD 0
TAX 0
PTRATIO 0
LSTAT 0
dtype: int64해당 데이터셋에는 결측치가 존재하지 않는다.
데이터 시각화
import matplotlib.pyplot as plt
plt.scatter(x['CRIM'], y, s=10)
plt.xlabel('CRIM')
plt.ylabel('Price')
plt.show()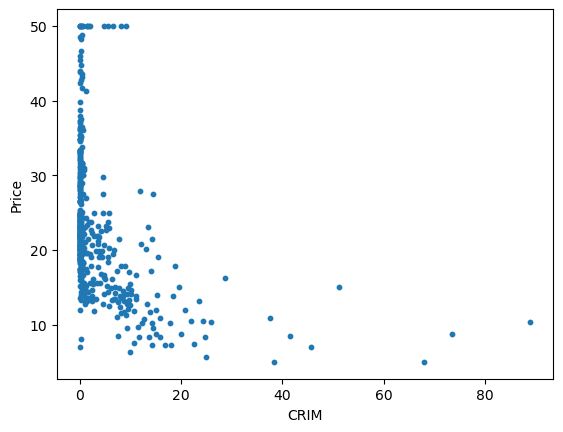
데이터 시각화 결과를 보면 조금 이상한 부분이 존재한다. 그래프 좌측 상단을 보면 값이 50.0인 데이터들이 칼로 자른 것 처럼 분포되어 있는 것을 볼 수 있는데, 이는 해당 데이터셋을 만들 때 50.0 이상인 데이터들의 값을 모두 50.0으로 처리한 것으로 보인다. 이러한 값들은 학습에 좋지 않은 영향을 줄 수 있기 때문에 이상치로 간주하고 삭제하는 것이 좋다.
데이터 전처리
값이 50.0인 데이터 삭제하기
값이 50.0인 데이터를 삭제하기 위해서는 우선 데이터와 정답지를 합치는 작업을 거쳐야 한다.
data = pd.concat([x, y], axis=1)
data = data[data['MEDV'] != 50.0]
data| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | LSTAT | MEDV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1 | 296.0 | 15.3 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2 | 242.0 | 17.8 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2 | 242.0 | 17.8 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3 | 222.0 | 18.7 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3 | 222.0 | 18.7 | 5.33 | 36.2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 501 | 0.06263 | 0.0 | 11.93 | 0 | 0.573 | 6.593 | 69.1 | 2.4786 | 1 | 273.0 | 21.0 | 9.67 | 22.4 |
| 502 | 0.04527 | 0.0 | 11.93 | 0 | 0.573 | 6.120 | 76.7 | 2.2875 | 1 | 273.0 | 21.0 | 9.08 | 20.6 |
| 503 | 0.06076 | 0.0 | 11.93 | 0 | 0.573 | 6.976 | 91.0 | 2.1675 | 1 | 273.0 | 21.0 | 5.64 | 23.9 |
| 504 | 0.10959 | 0.0 | 11.93 | 0 | 0.573 | 6.794 | 89.3 | 2.3889 | 1 | 273.0 | 21.0 | 6.48 | 22.0 |
| 505 | 0.04741 | 0.0 | 11.93 | 0 | 0.573 | 6.030 | 80.8 | 2.5050 | 1 | 273.0 | 21.0 | 7.88 | 11.9 |
490 rows × 13 columns
16개의 데이터가 줄어든 것을 확인할 수 있다. 이제 다시 시각화를 해보자.
plt.scatter(data['CRIM'], data['MEDV'], s=10)
plt.xlabel('CRIM')
plt.ylabel('Price')
plt.show()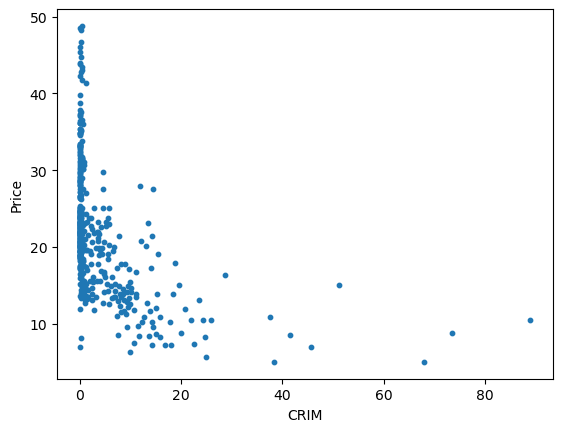
칼로 자른 듯한 부분이 깔끔하게 사라진 것을 확인할 수 있다.
데이터 Min-Max Scaling
데이터 스케일링을 위해서 합쳤던 데이터를 다시 나눠주자.
x = data.drop(['MEDV'], axis=1)
y = data['MEDV']
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
x = scaler.fit_transform(x)
x = pd.DataFrame(x, columns=data.columns[:-1])
x| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000000 | 0.18 | 0.058148 | 0.0 | 0.314815 | 0.577505 | 0.641607 | 0.268711 | 0.000000 | 0.208015 | 0.287234 | 0.083356 |
| 1 | 0.000236 | 0.00 | 0.234444 | 0.0 | 0.172840 | 0.547998 | 0.782698 | 0.348524 | 0.043478 | 0.104962 | 0.553191 | 0.198944 |
| 2 | 0.000236 | 0.00 | 0.234444 | 0.0 | 0.172840 | 0.694386 | 0.599382 | 0.348524 | 0.043478 | 0.104962 | 0.553191 | 0.056960 |
| 3 | 0.000293 | 0.00 | 0.053333 | 0.0 | 0.150206 | 0.658555 | 0.441813 | 0.448173 | 0.086957 | 0.066794 | 0.648936 | 0.026674 |
| 4 | 0.000705 | 0.00 | 0.053333 | 0.0 | 0.150206 | 0.687105 | 0.528321 | 0.448173 | 0.086957 | 0.066794 | 0.648936 | 0.093081 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 485 | 0.000633 | 0.00 | 0.414444 | 0.0 | 0.386831 | 0.580954 | 0.681771 | 0.122080 | 0.000000 | 0.164122 | 0.893617 | 0.213670 |
| 486 | 0.000438 | 0.00 | 0.414444 | 0.0 | 0.386831 | 0.490324 | 0.760041 | 0.104691 | 0.000000 | 0.164122 | 0.893617 | 0.197277 |
| 487 | 0.000612 | 0.00 | 0.414444 | 0.0 | 0.386831 | 0.654340 | 0.907312 | 0.093771 | 0.000000 | 0.164122 | 0.893617 | 0.101695 |
| 488 | 0.001161 | 0.00 | 0.414444 | 0.0 | 0.386831 | 0.619467 | 0.889804 | 0.113918 | 0.000000 | 0.164122 | 0.893617 | 0.125035 |
| 489 | 0.000462 | 0.00 | 0.414444 | 0.0 | 0.386831 | 0.473079 | 0.802266 | 0.124482 | 0.000000 | 0.164122 | 0.893617 | 0.163934 |
490 rows × 12 columns
데이터 스플릿
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0)
x_train.shape, x_test.shape, y_train.shape, y_test.shape((367, 12), (123, 12), (367,), (123,))모델링
모델 학습
보스턴 주택 가격 예측 데이터셋의 특성에 맞게 모델은 선형 회귀 모델로 선정하였다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(x_train, y_train)모델 예측
y_pred = lr.predict(x_test)
y_predarray([20.7849862 , 28.91512929, 20.07574554, 21.17500815, 19.83073573,
21.89763469, 31.87280547, 8.85456255, 17.88615521, 15.60012913,
37.33841001, 23.55920738, 31.03403016, 19.07390382, 36.55238918,
32.01792603, 15.45748715, 23.96898663, 21.43602168, 21.8068719 ,
34.2623474 , 17.88799224, 29.09895907, 24.30152493, 13.90149336,
30.12929038, 15.46315941, 22.35961453, 14.98790734, 33.46413923,
7.75997261, 23.56163233, 16.37996399, 28.01260792, 18.29263437,
21.81896334, 25.86003882, 20.55027182, 25.93696888, 24.94640758,
26.56550927, 25.24071843, 22.73325393, 16.7988142 , 20.95885581,
7.1645661 , 20.68386923, 18.87125015, 6.39731876, 18.32265984,
17.87360321, 18.88778991, 29.4508697 , 25.29438915, 23.98336479,
17.79404029, 21.25775539, 22.20871863, 23.40201463, 23.32065696,
12.45795651, 32.84298285, 35.5563624 , 22.8339334 , 27.71794575,
26.80733093, 24.13950932, 24.5513151 , 29.60681164, 20.0090581 ,
30.36155359, 29.33333847, 18.52451673, 7.04023296, 15.04253417,
10.19060853, 20.36180755, 16.99281677, 19.03538199, 34.28917953,
19.85160995, 21.0527815 , 9.65895928, 25.03434424, 17.57446444,
18.50027744, 16.44172213, 18.372733 , 22.60086592, 23.05748487,
22.56076945, 18.17941608, 31.55289642, 33.31033078, 13.87887184,
19.59843031, 19.18026467, 21.98485595, 13.04637074, 31.74602858,
11.71288512, 15.07167978, 20.49271949, 18.85158535, 22.66163837,
18.21508702, 6.03488717, 16.21720497, 26.57085197, 34.69481645,
21.50474309, 29.38206656, 11.93821218, 23.28130476, 11.44581252,
12.46879083, 29.78414219, 20.69335609, 22.81052563, 30.1421635 ,
30.6507055 , 16.99157418, 17.63698664])모델 평가
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(y_test, y_pred)
mse18.571034168594107
mse는 mean_squared_error로 평균제곱오차를 의미한다. 평균제곱오차는 말 그대로 오차를 제곱한 값들의 평균을 의미한다. 이는 평균적으로 실제 값과 얼만큼의 차이가 있는지 나타내고 값이 작을수록 실제 값과 차이가 적음을 의미한다.

