이 글은 diffusion의 초기 논문인 Deep Unsupervised Learning using Nonequilibrium Thermodynamics의 알고리즘 부분만을 정리한 글이다.

논문 : Deep Unsupervised Learning using
Nonequilibrium Thermodynamics

Introduction

Algorithm

algorithm의 목표는 복잡한 data distribution을 simple, tractable, distribution하면서도 생성 모델이 reversal을 학습 가능한 distribution으로 만드는 diffusion process를 구축하는 것이다.

용어정리

$x^{(0)}$ : initial data
$q(x^{(0)})$ : $x^{(0)}$의 probability density funciton(pdf)
$q(x^{(0 ... T)})$ : $q(x^{(0)}, ... , x^{(T)})$ : joint pdf
$p(x^{(T)})$ : $q(x^{(T)})$와 동일한 pdf 표기. 다만 동일한 time-step에서 forward process중인지 backward process중인지를 구분하기 위하여 각각 $q$, $p$으로 구분하여 표기.
$\pi (x^{(T)})$ : tractacle 하게 만든 distribution (forward process의 target)
$T_{\pi} ( y|y' ;\beta)$ : Markov diffusion kernel for $\pi (x^{(y)})$
$\beta$ : diffusion rate

Forward Trajectory

forward process의 목표는 initial data distribution $q(x^{(0)})$를 gradually하도록 analytically tractable한 distribution $\pi (x^{(T)})$로 변환하는 것이다.

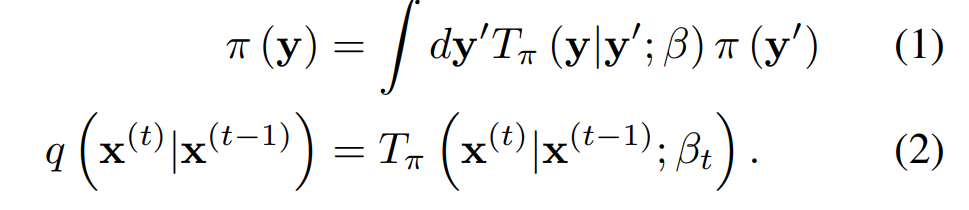
초기 데이터에서 diffusion process를 T step 시행한 후는 다음과 같다.

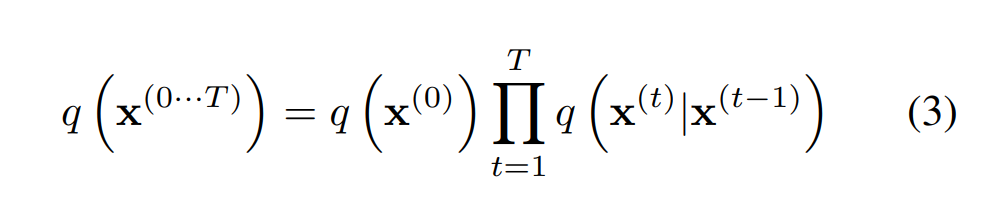
이때, $q(x^{(t)} | x^{(t-1)})$는 identity covariance를 가진 Gaussian distribution의 Gaussian diffusion, 혹은 binomial distribution의 binomial diffusion을 따른다.

실제 Gaussian diffusion 식은 다음과 같다.
$q(x^{(t)} | x^{(t-1)}) = \mathcal{N}(x^{(t)};x^{(t-1)} \sqrt{1-\beta _t}, \mathbf{I}\beta_t)$

Reverse Trajectory

학습을 위한 생성 모델은 Forward Trajectory 과정의 reversal이다. 먼저, 초기값으로 forward process를 통해 만든 tractacle하게 만든 distribution $\pi (x^{(T)})$를 설정한다.

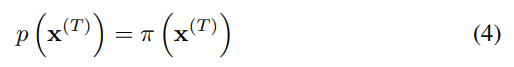
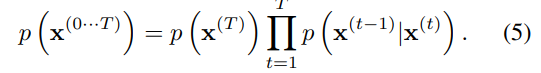
Gaussian과 binomial diffusion 둘 다 continuous할 때 ($\beta$가 충분히 작을 때) reversal process의 형태는 forward process와 같다. 따라서, process의 단계를 크게 하여 $\beta_t$가 충분히 작게 만들면 $q(x^{(t)} | x^{(t-1)})$의 reversal인 $p(x^{(t-1)} | x^{(t)})$도 Gaussian(binomial) 형태를 가지게 된다.

결국 Gaussian diffusion의 reversal도 Gaussian 형태이므로, reversal을 추정하기 위하여 각 time step reversal의 평균과 공분산을 추정하면 된다. 논문에서는 이를 추정하는 함수를 각각 $f_{\mu}(x^{(t)}, t)$, $f_{\sum}(x^{(t)}, t)$ 으로 만들어 이를 학습시킨다. Binomial의 경우 bit flip probability를 추정하는 함수 $f_{b}(x^{(t)}, t)$를 학습한다.

Model Probability

생성 모델이 생성한 데이터의 확률은 다음과 같다.

바로 적분하는 것은 난해하기에, annealed importance sampling과 Jarzynski equality를 이용하여 forward와 reverse의 relative probability를 계산한다. **annealed importance sampling, Jarzynski equality 내용 추가**

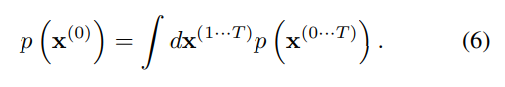
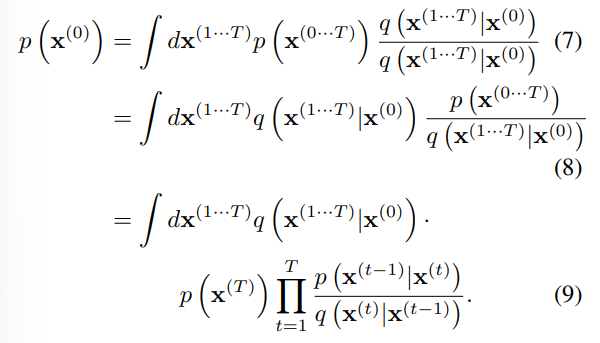
forward와 backward가 identical 하여 빠르게 계산가능하다...?

Training

학습 과정은 model의 log likelihood를 최대화하는 방식을 사용한다.

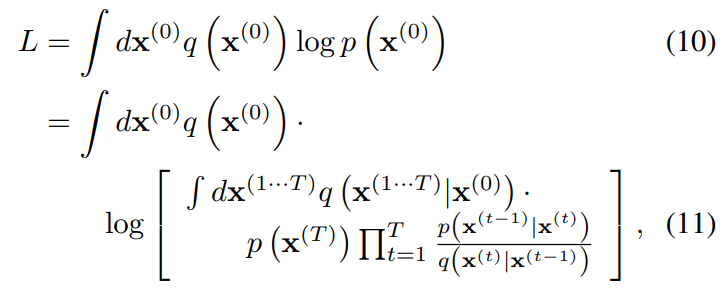
여기에 Jensen 부등식을 이용하면 다음과 같이 식을 변경할 수 있다.

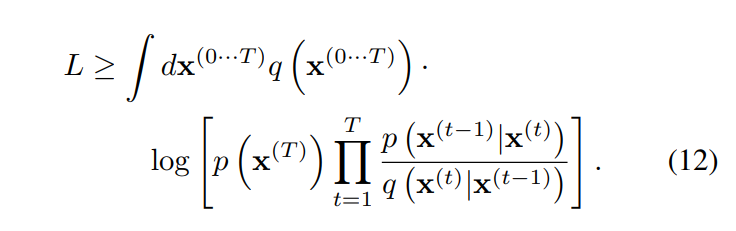
다시 Appendix B의 과정을 거치면, 아래와 같이 엔트로피와 KL divergence의 식으로 정리할 수 있다.

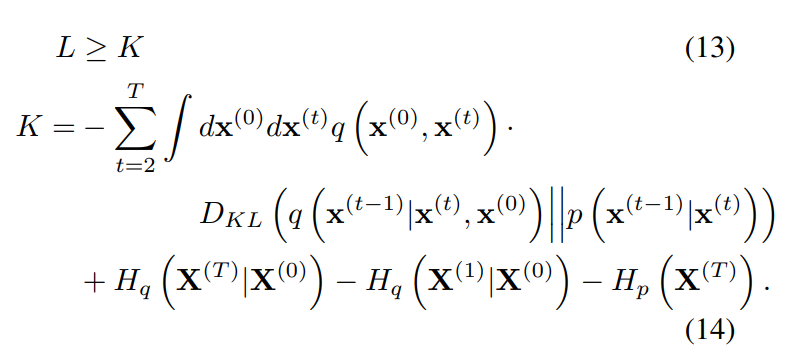
엔트로피와 KL divergence는 analytic하게 계산할 수 있다. 이러한 low bound를 유도하는 것은 variational Bayesian method의 log likelihood와 유사하다.

어떻게 계산가능하기에 analytic한가?
variational Bayesian method가 뭐길래 유사한가?

Training에서는 log likelihood의 lower bound를 최대화하는 reverse Markov transion을 찾는다.

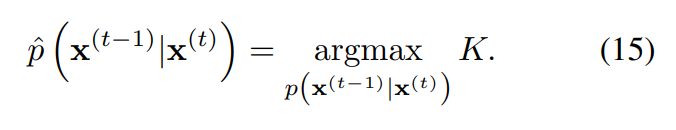
Diffusion Rate $\beta_t$ 설정

$\beta_t$를 설정하는 것은 전체 모델 성능에 큰 영향을 준다.
Gaussian diffusion의 경우 $\beta_1$은 overfitting을 막기 위한 작은 상수로, $\beta_{2...T}$는 K의 gradient ascent 과정에서 학습된다.

어떻게 학습되는가는 코드를 봐야 할듯

Binomial diffusion에서는 discrete state space 때문에 gradient ascent가 불가능하다. 대신 $\beta_t = (T-t+1)^{-1}$으로 설정하였다.

Multiplying Distributions, and Computing Posteriors

signal denoising이나 missing value를 찾기 위해 원래 분포 $p(x^{(0)})$에 다른 분포$r(x^{(0)})$를 multiplication하여 $\tilde{p}(x^{(0)}) \propto p(x^{(0)})r(x^{(0)})$를 이용하는 경우가 많다. 보통 이러한 방식은 난해하지만, diffusion에서는 이를 각 step의 small perturbation으로 두는 방식을 이용하여 편하게 계산할 수 있다.

먼저 새로운 분포 $\tilde{p}(\mathbf{x}^{(t)})$를 정의하자. 이 역시 확률분포이므로 normalize constant $\tilde{Z}_T$를 이용하여 다음과 같이 정의할 수 있다.

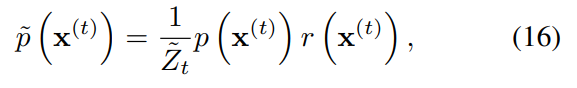
reverse process에서 Markov kernel 식은 다음과 같다.

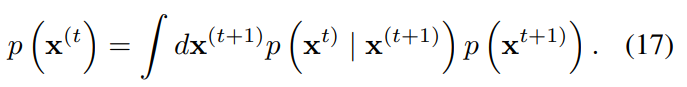
$\tilde{p}(\mathbf{x}^{(t)})$에서도 Markov kernel이 성립한다고 가정하고, 위 식에 대입하여 정리하면 아래와 같은 식을 얻을 수 있다.

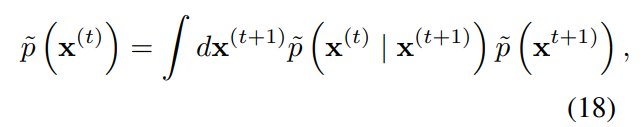
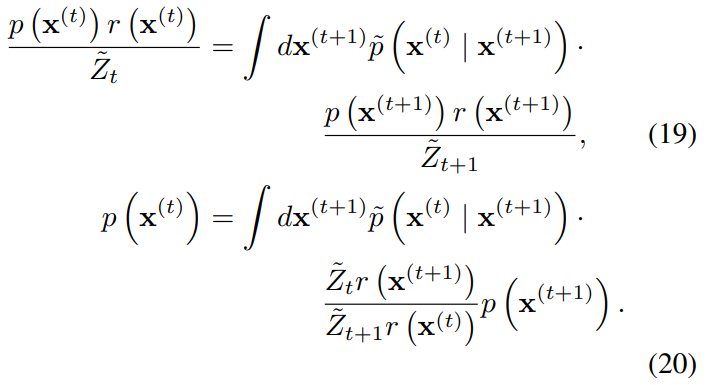
식을 정리해본 결과, 기존의 식과 유사한 식이 등장하였다. 만약 아래의 식이 성립한다면, reverse process의 식과 같아지므로 $\tilde{p}(\mathbf{x}^{(t)})$에서도 Markov kernel이 성립한다고 할 수 있다.

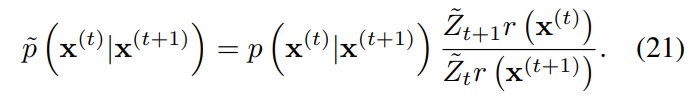
Gaussian에서 각 diffusion step의 $p(x^{(t)})$ 대부분의 $r(x^{(t)})$에 비하여 매우 작은 분산을 가진다. 때문에, $\frac{r(x^{(t)})}{r(x^{(t+1)})}$을 $p(x^{(t)})$의 작은 오류(perturbation)로 볼 수 있다. 이러한 판단 하에, 위의 등식은 대략적으로 성립한다.

$r(x^{(t)})$는 trajectory 동안 천천히 변화해야 하기에, 논문에서는 상수로 두었다. 다른 방법으로는 $r(x^{(t)}) = r(x^{(0)})^{\frac{T-t}{T}}$의 형태로 둘 수도 있다.

Reverse Process의 Entrophy

forward를 알고 있기 때문에 reverse process의 각 step의 upper/lower bound를 위와 같이 계산할 수 있다. 각 값이 $q\left(\mathbf{x}^{(1 \cdots T)} \mid \mathbf{x}^{(0)}\right)$만으로 계산할 수 있으므로 analatic 하게 계산 가능하다.

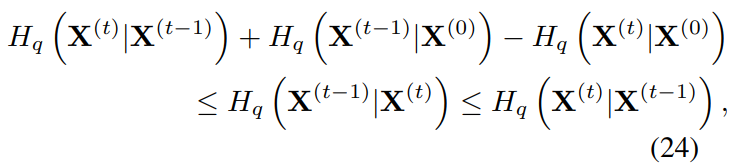
Some additional appendix

Table A

Appendix B

Training 과정에서 요약된 log likelihood를 Entrophy와 KL divergence의 식으로 정리하는 과정.

B.1 $p(\mathbf{X^{(T)}})$의 엔트로피

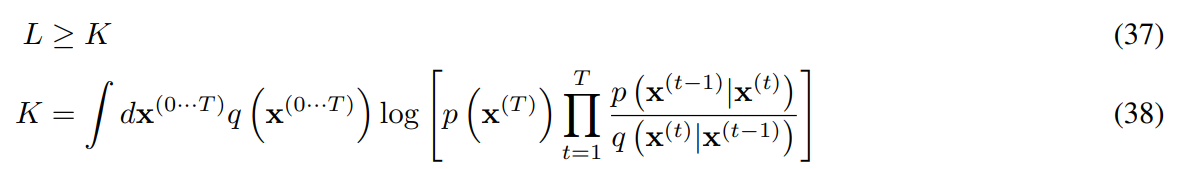
각 $q(\mathbf{x}^{(t)})$는 pdf이므로 log를 분리하면 뒷부분 항에서 $\int{d\mathbf{x^{(t)}} \,q(\mathbf{x^{(t)}})} =1$ 이므로 T 항만 남고 정리된다.

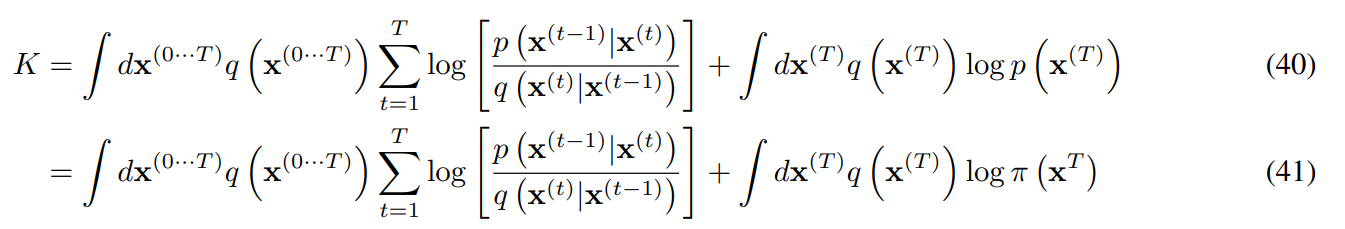
위에서 $\pi(\mathbf{x}^{(t)})$의 cross entrophy는 $p(\mathbf{x}^{(T)})$의 entrophy와 같은 상수이다. 따라서

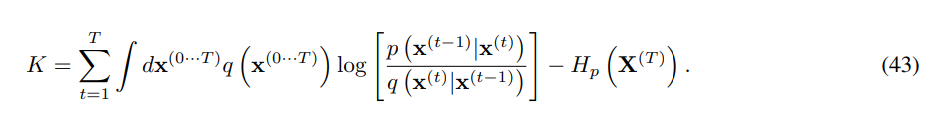
이 성립한다.

B.2 t = 0일때 edge effect 제거

edge effect를 제거하기 위하여 reverse의 마지막 step을 상응하는 forward diffusion step과 동일하게 둔다.

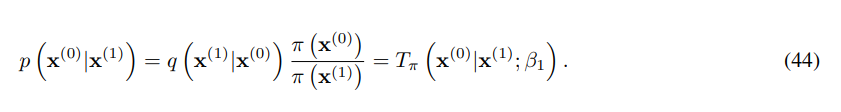
이를 위 식에 대입하면 다음과 같다. $\pi(\mathbf{x}^{(t)})$의 cross entrophy
$H_p(X^{(T)}) = -\int{d \mathbf{x}^{(t)} q(\mathbf{x}^{(t)} \log{\pi}(\mathbf{x}^{(t)})}$ 가 상수임을 이용하면 (45)의 중앙의 항이 서로 상쇄되어 (46)처럼 정리된다.

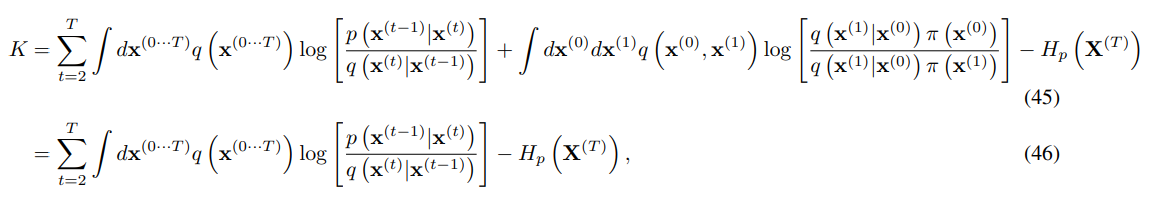
B.3 $q(x^{(t-1)} | x^{(0)})$ 항 이용

forward trajectory가 Markov process이므로 아래 식과 같이 변형할 수 있다.

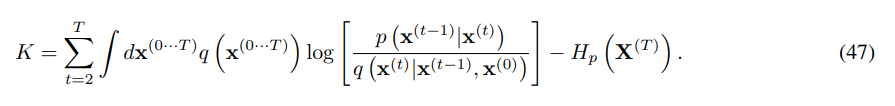
Bayes' rule을 이용하여 다음과 같이 정리된다.

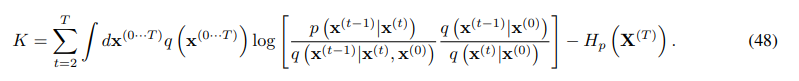
B.4 KL divergences와 Entrophy로 다시쓰기

log의 부분항을 나누고 적분의 무관한 항을 정리하면 일부를 조건부 엔드로피 식으로 정리가능하다.

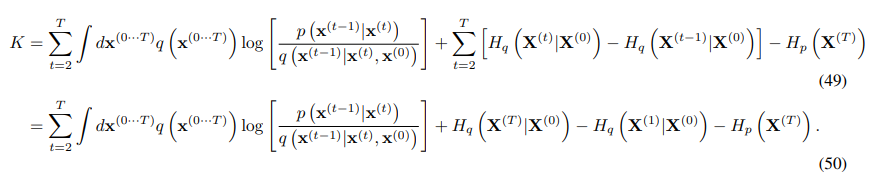
이후 log 항을 KL divergence를 이용하여 정리하면 아래의 식으로 정리할 수 있다.

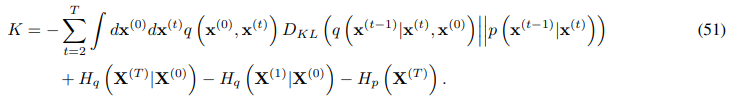
$\mathbf{x}^{(0)}$과 $\mathbf{x}^{(t)}$를 알고 있으므로, KL divergence항과 엔트로피를 analatic하게 계산할 수 있다.