딥러닝 기초 (1)

gmlwlswldbs·2021년 9월 28일

스터디

목록 보기

5/19

1. 인공지능 / 머신러닝 / 딥러닝

💡 인공지능 ⊃ 머신러닝 ⊃ 딥러닝

📌 인공지능

인텔리전트한 기계를 만드는 과학과 공학 (명확한 정의가 없음. 포괄적인 개념)
컴퓨터가 학습할 수 있도록 구현한 알고리즘

📌 머신러닝

컴퓨터가 명시적으로 프로그램되지 않고도 학습할 수 있도록 하는 연구 분야 / 만약 어떤 작업 T에서 경험 E를 통해 성능 측정 방법인 P로 측정했을 때 성능이 향상된다면 이 프로그램은 학습은 한다고 한다.
인공신경망을 얕게 활용한다
분류(Classification)와 회귀(Regression)문제로 구분

📌 딥러닝

인간의 신경망을 모방한 인공신경망의 한 종류
충분히 깊은 인공 신경망을 학습하는 머신러닝의 기법

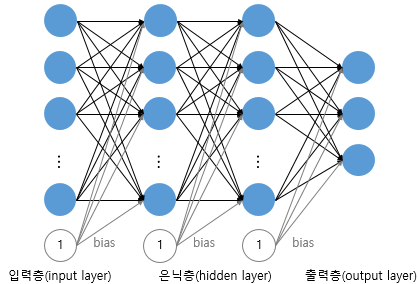
2. 신경망

📌 퍼셉트론 (Perceptron)

신경망의 기원이 되는 알고리즘

x : 입력값 w : 가중치 y : 출력값 원 : 인공뉴런

각 입력값이 가중치와 곱해져 인공 뉴련에 보내지고 출력값이 된다
임계치(활성화함수 사용)를 기준으로 출력값이 0 또는 1(또는 다른)의 값을 가진다
단층 퍼셉트론으로 AND, OR, NAND 게이트를 모두 구현할 수 있지만 XOR 게이트는 구현할 수 없다.

💡 그래프를 생각해보면 출력값이 1이 되는 경우와 0이 되는 경우를 하나의 직선으로 나눌 수 없다 = 비선형 영역으로는 분리 가능하다 => 다층 퍼셉트론 사용
💡 단층 퍼셉트론은 선형 영역에 대해서만 분리 가능하다. (그래프 속 출력값을 하나의 직선으로 나눌 수 있다)

📌 신경망 구조

다층 퍼셉트론 (MLP, MultiLayer Perceptron)
- 입력층과 출력층 중간에 여러 층 추가 (은닉층, hidden layer)
- 위에서 말한 XOR 게이트는 퍼셉트론 층을 여러개 쌓아 AND, NAND, OR 게이트를 조합하여 구현 가능하다.
심층 신경망 (DNN, Deep Neural Network)
- 은닉층이 2개 이상인 신경망
- 기계가 스스로 정답을 찾기 위한 가중치를 찾아 내는 것을 머신러닝에서의 학습이라고 하고 이 과정에서 손실 함수와 옵티마이저를 사용한다.
  💡 딥러닝 : 학습 시키는 인공 신경망이 심층 신경망일 경우

📌 활성화 함수

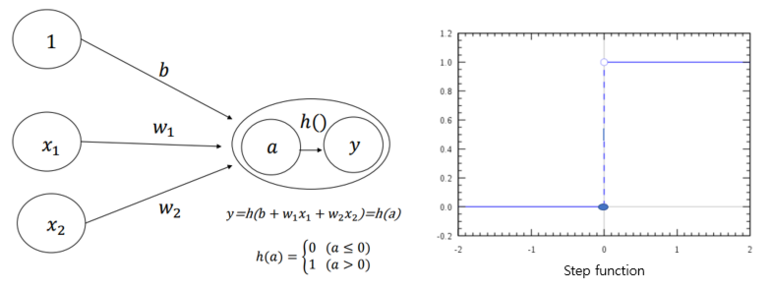
활성화 함수 : 은닉층과 출력층의 뉴런에서 출력값을 결정하는 함수 (ex. step function)
💡 비선형 함수(직선 1개로 그릴 수 없는 함수)여야 한다. 선형함수의 경우 계속 합성해도 결국에는 선형함수가 되기 때문에 은닉층을 여러 개 쌓는다고 가정하더라도 1개 쌓는 것과 같다. 따라서 은닉층을 여러 층 쌓을 수 없기 때문에 선형함수를 쓰지 않는다.
💡 편향 (Bias) : 연산을 거친 결과가 바로 최종신호로 가는 것이 아닌 어떤 조건(Bias)가 걸려있는 (활성화)함수를 거친 값을 최종신호로 보낸다

1. 시그모이드

기울기 (위 이미지에서는 세로축)가 0 또는 1에 가까워질수록 기울기가 완만(0에 가까워짐)해지는 함수
💡 기울기 소실 문제 : 은닉층이 깊어지면 역전파 과정에서 출력층에 가까운 층의 기울기는 잘 전파되지만 앞단에는 매우 작은 기울기가 계속 곱해지기 때문에 잘 전파되지 않는 문제가 생긴다. (가중치 W가 업데이트되지 않아 학습이 잘 되지 않음)

2. tanh(Hyperbolic tangent function)

입력값을 -1과 1 사이의 값으로 변환하는 함수
💡 -1과 1로 갈수록 기울기가 0에 가까워지기 때문에 시그모이드와 마찬가지로 기울기 소실 문제가 생긴다. 하지만 시그모이드와 달리 0을 중심으로 하고 반환값의 변화폭이 비교적 크기 대문에 기울기 소실이 덜하기 하다.(????)

3. ReLU(Rectiied Linear Unit)

음수 입력시 0, 양수 입력시 입력값 그대로 출력하는 함수 f(x) = max(0, x)
특정 양수 값에 수렴하는 형태가 아니므로 깊은 은닉층을 가진 신경망에서 시그모이드보다 잘 작동한다.
죽은 렐루 (Dying ReLu) : 입력값이 음수일 때 기울기가 0이 되어 뉴런이 회생하기 어려운 상태가 되는 것

4. Leaky ReLU

ReLu를 변형한 함수. f(x) = max(ax, x). 죽은 렐루 문제를 해결하기 위해 입력값이 음수일 때 0.001과 같이 매우 작은 수를 출력하도록 하였다.
a의 값은 매우 작게 설정(음수일 때 기울기). 일반적으로 0.01

5. 소프트맥스. Softmax

출력층에서 주로 사용되는 함수

3. 신경망 학습

📌 손실함수 (Loss Function)

실제값과 예측값의 차이를 수치화해주는 함수
오차가 클수록 손실함수의 값이 크고 오차가 작을수록 손실함수의 값이 작다
오차를 지표로 미분 가능하며 큰 차이를 유발하는 함수를 손실함수로 사용
- Loss의 기울기값을 통해 파라미터를 조정하여 0으로 이동시키기 위해 쓴다
- 정확도를 지표로 사용시 미분 불가능하거나 대부분 상태에서 값이 0이기 때문에 오차를 지표로 사용한다
회귀에서는 MSE, 분류에서는 CE를 주로 쓴다
딥러닝의 학습 과정은 손실함수의 값을 최소화하는 W와 b를 찾는 것이기 때문에 손실함수는 매우 중요한 역할을 한다

1. 평균 제곱 오차 (MSE, Mean Squared Error)

제곱하는 이유 : 실제값과 예측값의 차이가 크면 loss값이 커지고 오차가 두드러지는 부분을 크게 나타내기 위해
연속형 변수 예측

2. 교차 엔트로피 오차 (CE, Cross Entropy Error)

tk : 실제값(0 또는 1) yk : 예측값(확률)

📌 경사하강법 (Gradient Descent)

함수 값이 작아지는 방향으로 변수값을 변형시켜가며 최종적으로 최소 함수값을 찾도록 하는 방법

위 함수에서

기울기가 음수일 때 x값이 증가하는 방향
기울기가 양수일 때 x값이 감소하는 방향

Step Size

위의 기울기에 따른 x값 방향을 수식으로 나타낸 것

미분값이 극소값에 가까울수록 이동거리에 크게 영향을 받는다
- 미분값이 극소값에 가까울수록 작아지고 멀어질수록 커진다
이동거리의 조정값을 step size(α) 라고 정한다
- 이동거리에 사용할 값을 기울기와 비례하는 조정값으로 표현해서 현재 x가 극소값에서 멀면 많이 이동, 가까우면 적게 이동시킬 수 있게 이동거리 조정값 (step size, α) 으로 표현
= learning rate

적절한 크기의 Step Size

step size가 클 경우 : 많이씩 이동하기 때문에 최소값을 향해 빠르게 수렴 가능 but 너무 크면 수렴을 못하고 함수값이 계속 커지기만하는 방향으로 최적화 (발산)
step size 가 작을 경우 : 위와 같은 문제는 일어나지 않지만 최적화하는데 시간이 많이 걸린다

💡 Local minima 문제 : 경사하강법을 사용할 경우 생길 수 있는 문제. 초기값이 랜덤하게 설정되기 때문에 global minimum을 찾지 못하고 lacal minima를 찾는 것에서 최적화를 끝낼 수 있다.

📌 최적화 (Optimization)

1. 확률적 경사 하강법 (Stochastic Gradient Descent, SGD)

전체 데이터가 아닌 랜덤 선택한 하나의 데이터에 대해서만 그래디언트 계산
단순하고 빠르다는 장점이 있지만 매개변수 변경폭이 불안정함 (local minima에 빠졌을 때 빠져나오기는 쉽지만 global minimum에 도달하기는 어렵다)
비효율적 탐색 경로 : high cost
문제점 개선을 위해 일정량의 데이터에 대해서만 매개변수 값을 조정하는 미니 배치 경사하강법을 사용한다

2. 모멘텀 경사 하강법 (Momentum Gradient Descent)