소프트맥스 역전파

추가로 정리

📌 순전파

입력 : (z1, z2, z3)
softmax 층 출력 : (y1, y2, y3)
cross entropy 층 정답 레이블 : (t1, t2, t3)
cross entropy 층 출력 : L (손실)

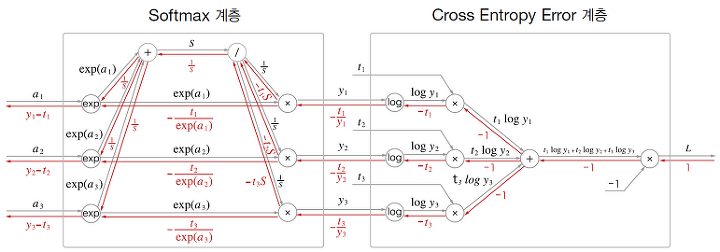
1. Softmax 계층

• 입력값을 0~1사이의 값으로 정규화하여 출력의 총합을 1을 만드는 함수
• exp 노드 : 양수로 만들어주기 위해서 각 값에 exp를 취한다
• 덧셈 노드 (위) : 합이 1이 되기 하기 위해서 각 exp를 취한 값을 다 더해서(덧셈 노드 통과) 합(S)을 만든다.
• 곱셈 노드 (위) : 역수를 취해서 곱해 준다. -> 각각 확률분포 y1 y2 y3 가 생긴다.

2. Cross Entropy 계층

• Softmax 계층의 출력값과 정답 레이블을 통해 loss 계산 (손실함수)
• log노드 통과 -> t값 곱해줌(곱셈노드) -> 전부 다 더해줌 -> -1 곱해줌

📌 역전파

1부터 출발 (ϑL/ϑL=1)

• 덧셈 노드의 역전파 : 입력값 그대로 출력
• 곱셈 노드의 역전파 : 미분값에 순전파로 노드로 들어온 입력값을 바꾼 것을 곱해서 출력
• log 노드의 역전파 : y = logx 미분해서 1/x 출력

1. Cross Entropy 계층

곱셈 - 덧셈 - 곱셈 - 로그 노드의 순서대로 계산하면 출력이 (−t1/y1,−t2/y2,−t3/y3) 이 되고 이 값은 소프트맥스 계층의 입력으로 흘러 들어간다.

2. Softmax 계층

곱셈노드 : 순전파 입력값을 바꿔서 출력

• 위쪽

• 아래쪽

나눗셈 노드 : t1 + t2 + t3 = 1 (원핫벡터)

덧셈 노드 : 입력 그대로 출력

exp 노드 : 두 역전파 입력 값에 미분값인 exp(a1) 곱함

결과적으로 (y1 - t1, y2 - t2, y3 - t3) 즉 softmax의 결과값 y에서 정답 레이블을 뺀 값이 역전파로 들어온다.