딥러닝을 배우기 시작한 후 많이 듣는 이야기가 선형대수학과 미분을 잘 알면 좋다는 이야기였다. 그래서 나도 많은 경로로 선형대수학에 대해 공부를 했다. 블로그를 시작한 김에 간단하게 선형대수학 내용을 정리해두려한다.

• 3Blue1Brown - Essence of Linear Algebra
• Youtube 이상엽 선형대수학
• numpy exercises by Kyubyong

# KEYWORD
MAGNITUDE, NORM, DOT PRODUCT, DETERMINANT, ⭐LINEAR TRANSFORM⭐
COVARIANCE, CORRELATION COEFFICIENT, BASIS, SPAN, RANK, ⭐PROJECTION⭐
EIGENVECTOR, EIGENVALUE, PCA

numpy.linalg

Notation 헷갈리지 말자

1. $\vec{x}$ : vector
2. $\left\| \vec{x} \right\|$ : norm
3. $|\vec{x}|$ or $det(\vec{x})$ : determinant
4. $\vec{x}\cdot\vec{y}$ : dot product
5. $\vec{x}^T$ : transpose

Dot Product (내적)

두 벡터의 내적은 각 구성요소의 곱을 모두 합하거나 두 벡터의 norm과 두 벡터가 이루는 사이각의 곱으로 구할 수 있다.

만약 두 벡터가 수직을 이룬다면 내적은 0이된다

Determinant

판별식. 고등학교때는 0이 아니면 역행렬이 존재한다 라고까지만 배웠다.
Linear transform과 어떤 연관이 있는지 알아두자
좌표상의 벡터에 대해서 기저가 이루는 단위 (2차원 벡터라면 사각형)가 얼마나 scaling되는지를 의미한다.
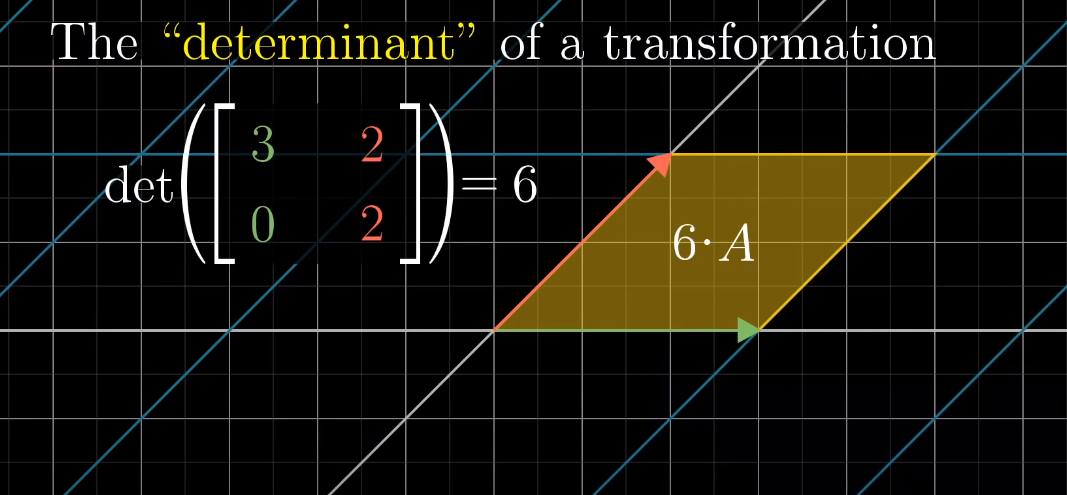3Blue1Brown - Essence of Linear Algebra Chapter 6 Determinant 참고

위 벡터 $A = \begin{pmatrix} 3 & 2 \\ 0 & 2 \end{pmatrix}$에서 기저 중 하나는 $(1, 0)$과 $(0, 1)$이다. 이 둘이 이루는 면적은 1인데, $A$의 determinant가 6이므로 기저가 이루는 면적의 6배만큼 scaling된 것을 확인할 수 있다.

---

Covariacne

Correlation Coefficient