AVL트리

seonghun park·2022년 6월 2일

자료구조

AVL Tree란?

AVL트리란 스스로 균형을 잡아주는 트리이다.
AVL트리는 BST의 일종으로 트리의 h에 따라 수행시간이 결정되는 BST특성에서 O(n)이 되지 않도록 잡아주는 역할을 한다.
이를 위해서 중요한 조건을 만족한다.

자식의 높이 차가 최대 1이다.

AVL트리의 높이

n개의 키를 저장하는 AVL 트리의 height는 O(log n)이다.
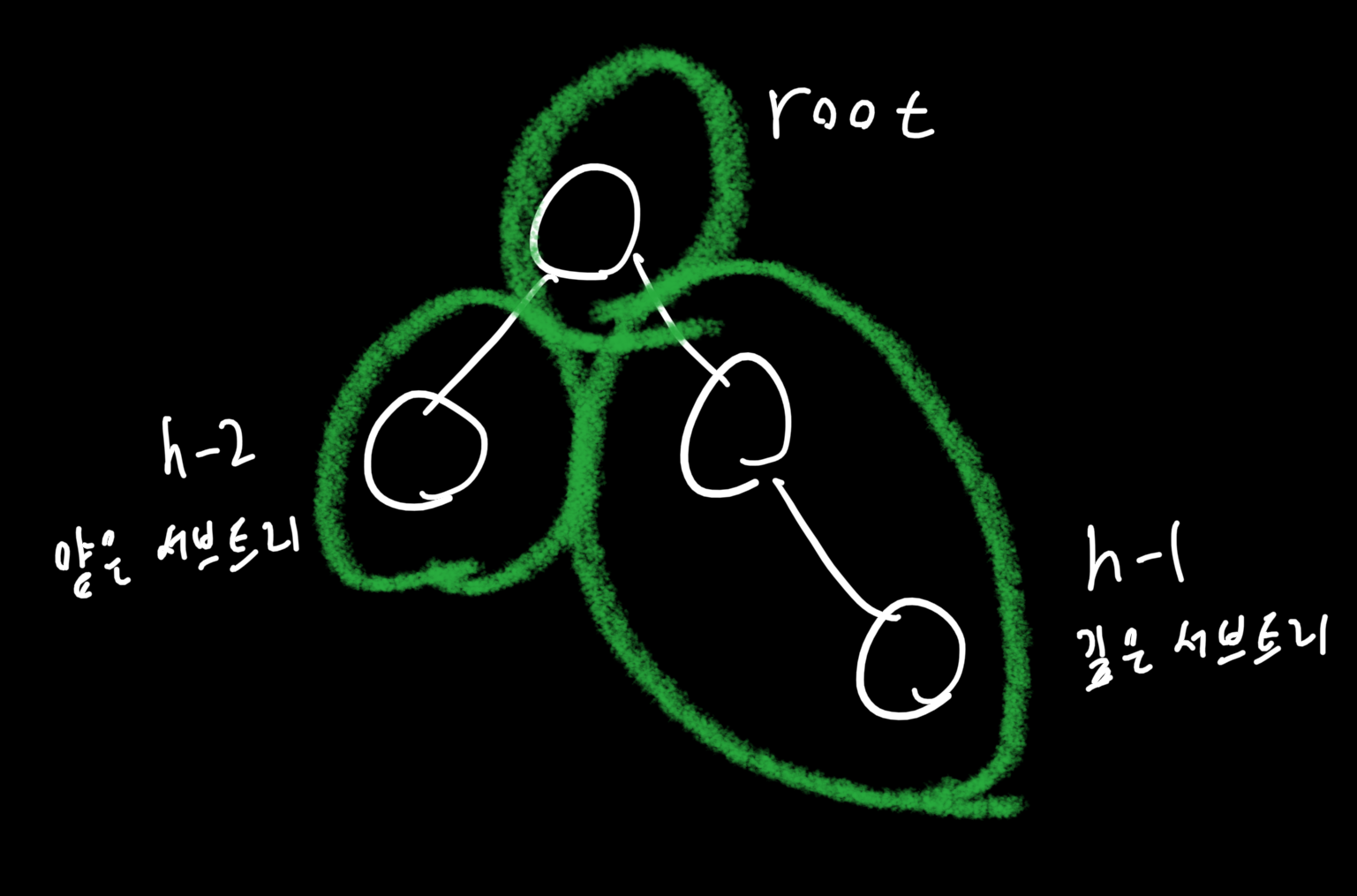
증명: 인터널 노드의 최소 수 n(h)도입
n(1) = 1, n(2) = 2
n>2에 대하여, 루트 노드 + 깊은 서브트리 + 낮은 서브트리 == 1 + n(h-1) + n(h-2).

예시로 h가 3일 때 최소 인터널 노드의 개수 n(3)을 구해보자.

이 페이지를 이해하기 위해 다음 증명식을 참고하자.

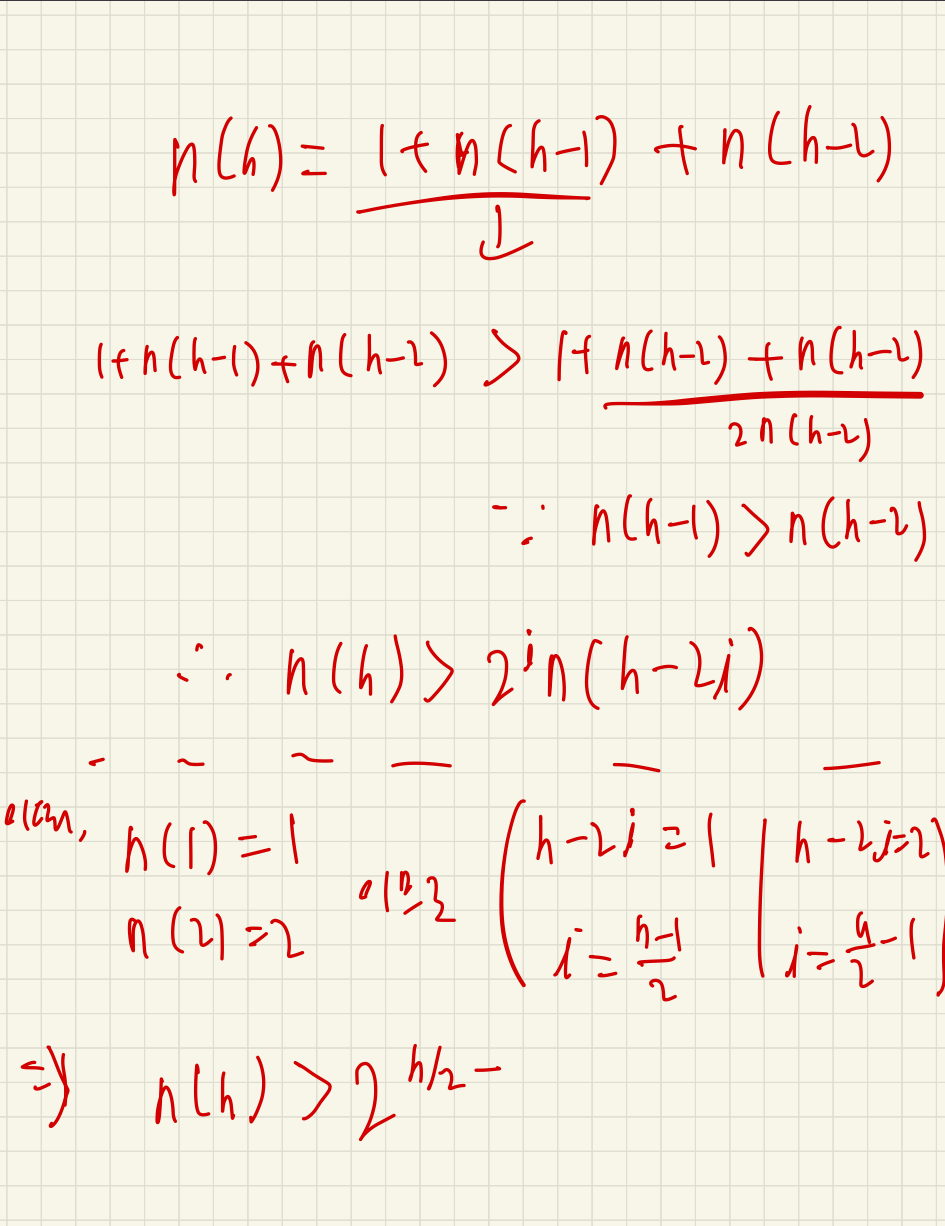
Insertion

삽입은 이진탐색트리를 이용한다.
항상 leaf노드 두개를 추가해주어야 한다.
위반된 순서균형을 맞추기 위해 Restrucuring과정을 수행한다.
- 이를 위해 zyx, abc를 규정해주어야 한다는 것을 유념하고 다음을 보자

z = 균형이 맞지 않는 레벨의 internal 노드 (insert와 removal의 결과로 예측한 결과이기에 틀릴 수도 있다.)
y = z의 자식 중 height가 높은 것
x = y의 자식 중 height가 높은 것

abc 순서 -> inorder 순서

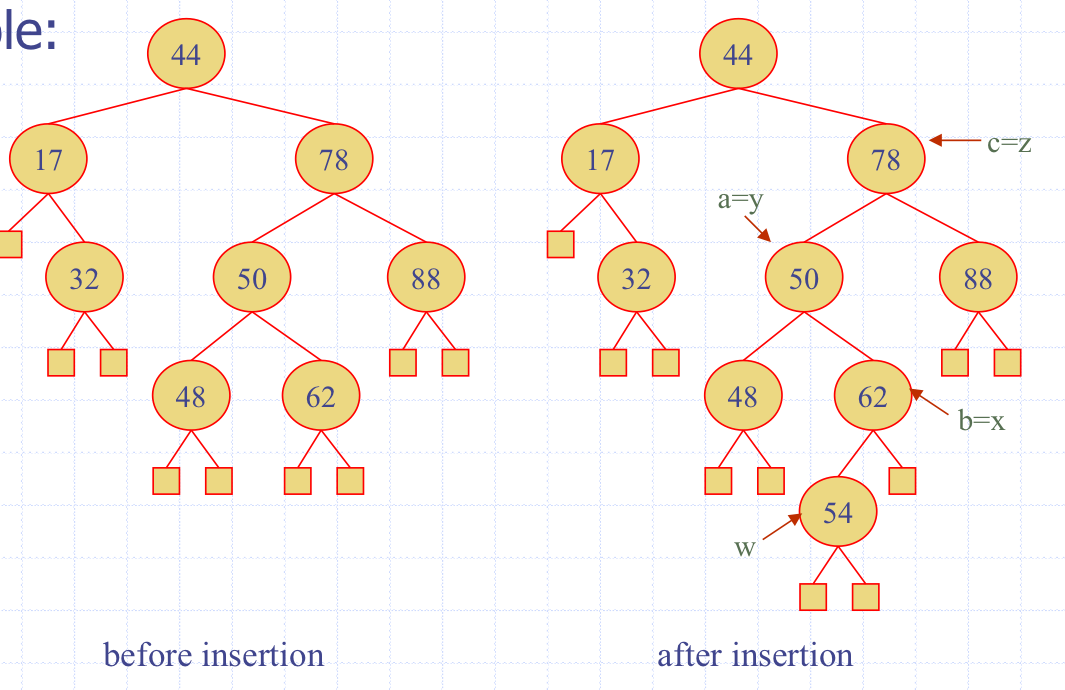
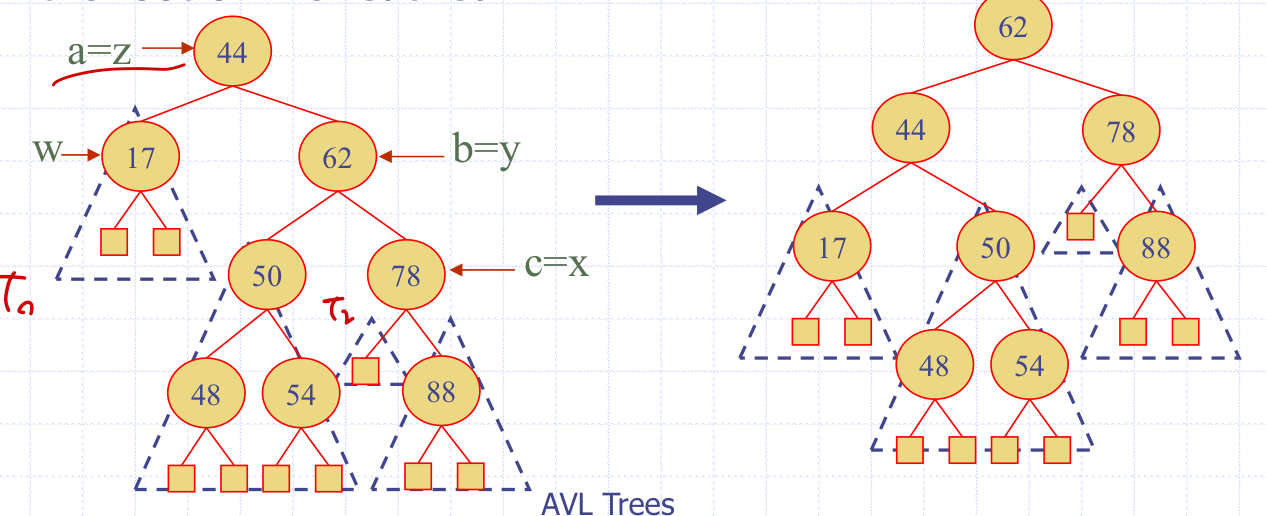
위 그림은 54를 삽입한 예시이다.
먼저 이진탐색트리의 규칙을 통해 숫자를 삽입한다.
하지만 레벨1과 레벨2에서 AVL트리의 height규칙을 위반한 것을 알 수 있다.
아래서부터 시작해서 처음 균형이 어긋난 노도의 parent를 z, 그 후로 순서를 메긴다.
또한 inorder에 맞게 a~ 순서를 메긴다.
아래 그림처럼 restructuring

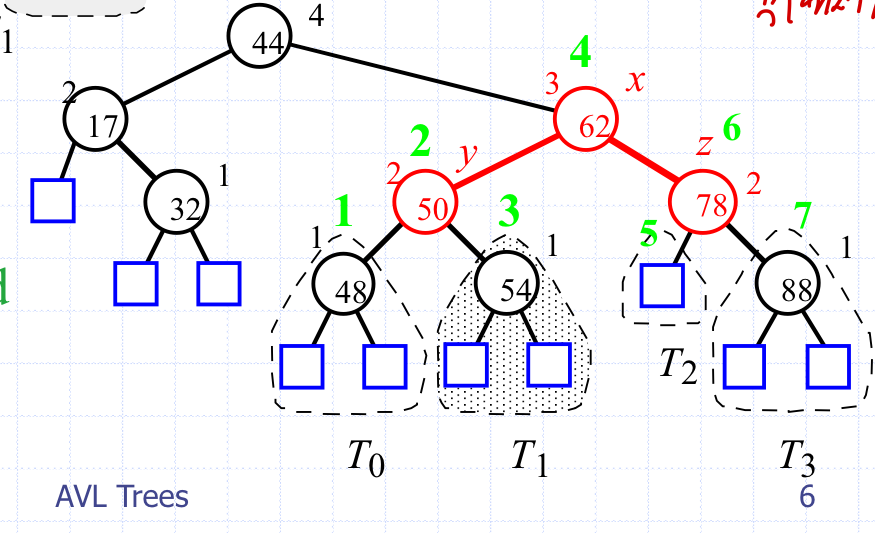
이때 서브트리가
하나만 이동하는 것을 -> single rotation
두개가 이동하는 것을 -> double rotation 이라 함.

결과적으로 AVL트리의 삽입 = 이진탐색트리 + restructuring 이다.

1) binary search tree 와 동일한 방법으로 삽입 ⇒ O(log n)
2) 삽입한 곳으로부터 올라가며 문제가 발생하는지 확인 ⇒ O(log n)
3) z,y,x 크기 비교, a,b,c 설정 ⇒ O(1)
4) 서브트리 T1 or T1, T2 옮기기 ⇒ O(1)
의 과정을 거치므로 총 수행시간은 "O(log n)" 이 된다.