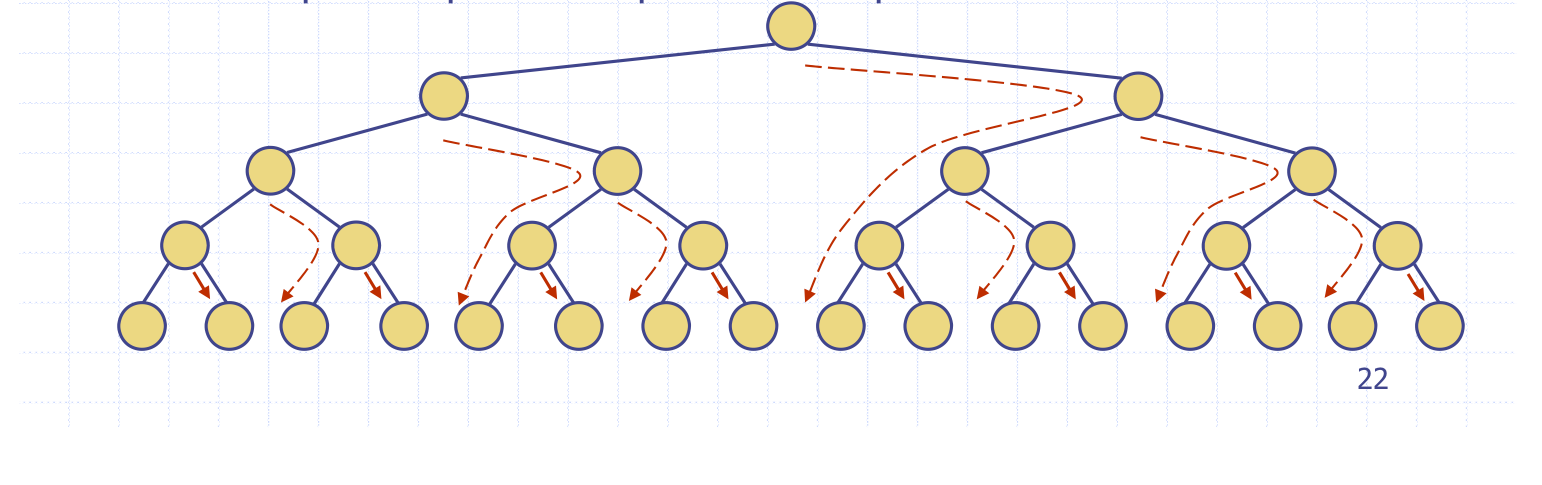
Binary Search Trees

Binary Search Trees란?

• 이진탐색트리는 key-value를 저장하는 이진 트리이다.
• internal노드에 Item을 저장하고,external노드에는 저장하지 않는다.
• 중위선회를 통해 값을 얻는다.
• u - v - w 로 연결된 트리가 있다면 key(u) <= key(v) <= key(w) 를 만족한다.

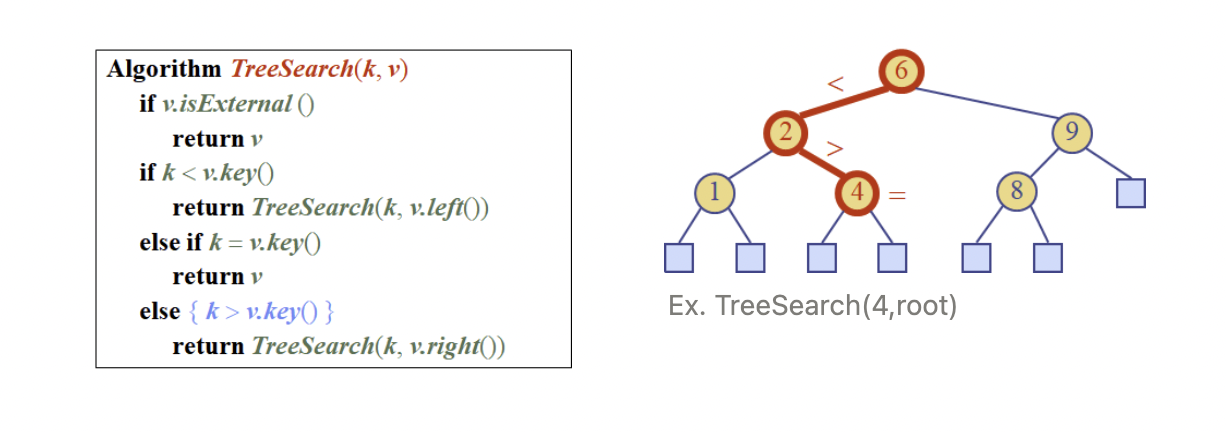
Search

찾고자 하는 key k를 찾기 위해 탐색을 시작할 노드 v부터 탐색을 시작한다. (보통은 루트노드부터)
찾고자 하는 값이 더 작으면 왼쪽으로, 크면 오른쪽으로 이동한다.
만약 우리가 leaf노드에 도달하면 찾고자 하는 key가 존재하지 않는 것이다.
최악의 경우 리프노드까지 탐색을 진행하므로 트리의 높이만큼의 시간복잡도를 갖는다.

Insertion

insert(k,e)

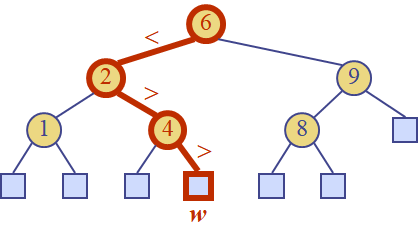
주의할 점은 반드시 말단노드까지 내려간다는 점이다.
따라서 트리의 높이만큼의 시간복잡도를 갖는다.

deletion

erase(k)
삭제연산은 조금 까다롭다.

1. 삭제하려는 노도의 자식들이 둘다 말단일 경우
   해당 노드와 말단노드 삭제 -> 남은 말단 노드를 부모 노드와 연결
   -> O(n)

2. 하나만 말단 노드일 경우
   
   해당 노드와 말단노드 삭제 -> 남은 자신노드(internode)를 부모노드와 연결
   -> O(n)

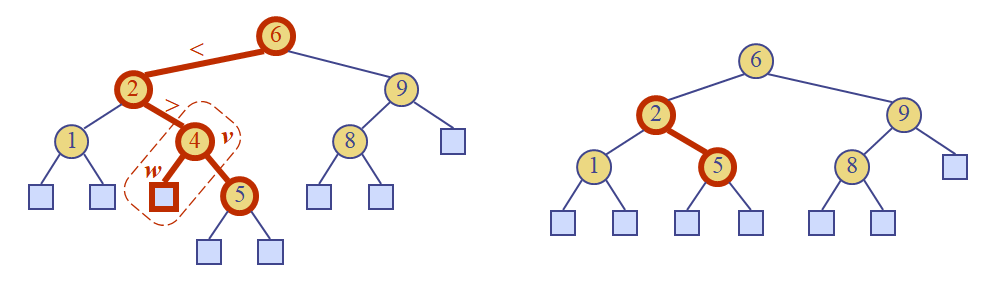
3. 둘 다 internal노드일 경우
   
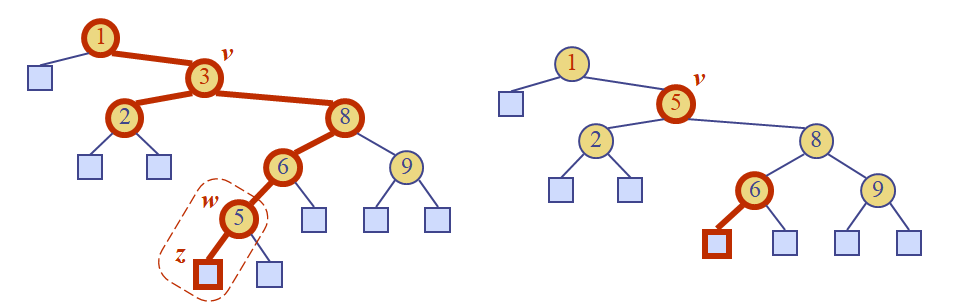
   삭제할 노드 v의 inorder순서 바로 다음 주자의 키 값을 복사해서 v에 덮어씌운다.

   여기서 다음 주자를 successor라고 부르고, 삭제할 노드의 오른쪽 자식에서 말단을 만날때까지 왼쪽으로 가면 successor를 찾을 수 있다.

succesor노드 w와 그의 왼쪽 리프노드를 제거한다.

performance

find, insert, erase는 O(h)의 시간복잡도를 갖는다.
이 말은 즉, 트리의 생김새에 따라 수행시간이 달라진다는 뜻이다.

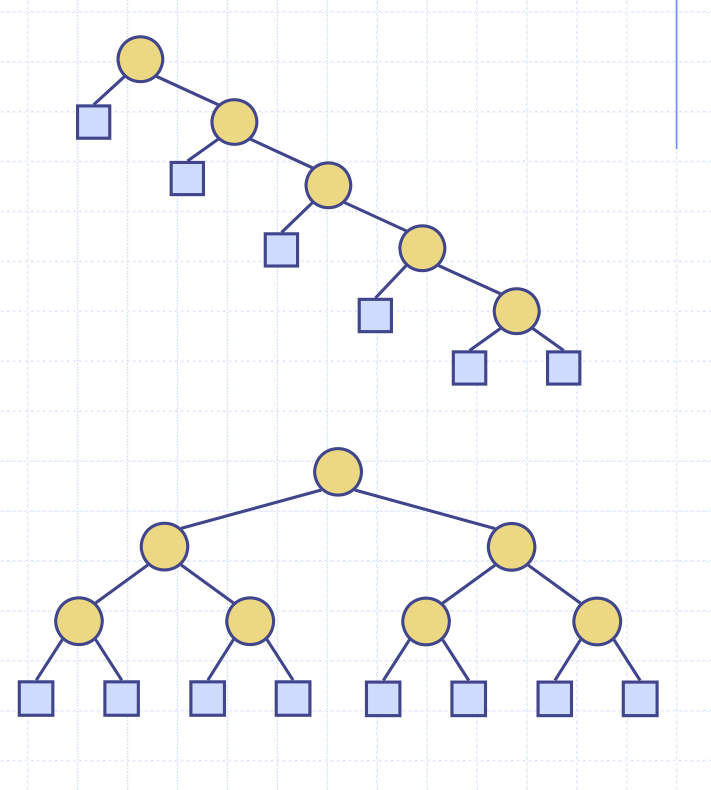
최악의 경우 위의 트리처럼 O(n)이 걸리고, 이상적인 경우 아래 그림처럼 O(log n)이 걸린다.

이를 해결하기 위해 AVL트리라는 것을 배워보자.