BFS

BFS(Breadth-First Search)란?

->너비우선탐색

• BFS는 그래프의 깊이보다는 너비를 우선적으로 탐색하는 알고리즘이다.
• 시작 정점으로부터 가까운 정점들을 우선적으로 방문하고 그 후에 떨어져 있는 정점들을 방문한다.
• 큐를 이용한다.
  

---

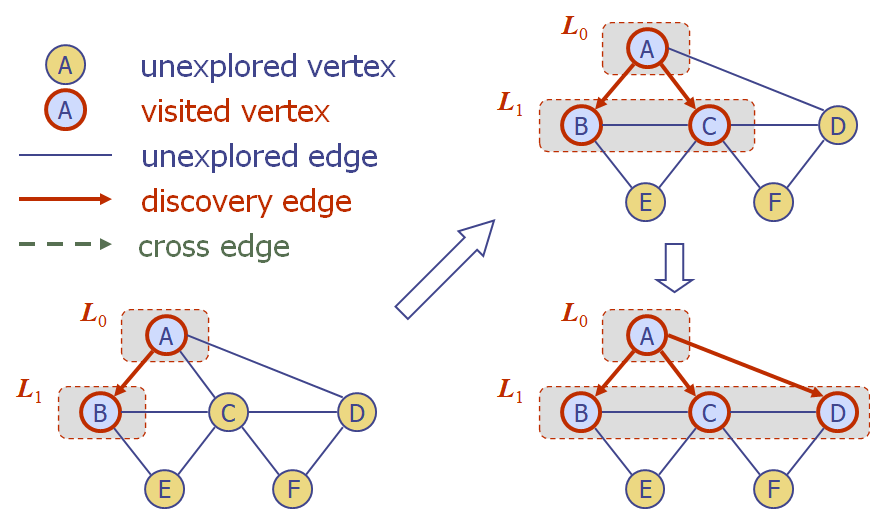
BFS알고리즘

DFS알고리즘에서도 역시 정점과 간선의 방문상태를 점검하기 위해 "label"이라는 개념은 도입한다.

• 정점
  -> unexplored: 방문되지 않은 초기 상태
  -> visited: 방문된 상태
• 간선
  -> unexplored: 방문되지 않은 초기 상태
  -> Discovery: 방문된 상태
  -> Cross: 정점이 방문된 상태로 가려할 때

(좌) BFS(G)
-> {v,e}입력으로 그래프 G를 삽입한 후, 정점과 간선들을 모두 초기상태로 초기화한다.

(우) BFS(G,s)
말로 설명하기에는 장황하니 코드와 예시를 보며 이해하자

---

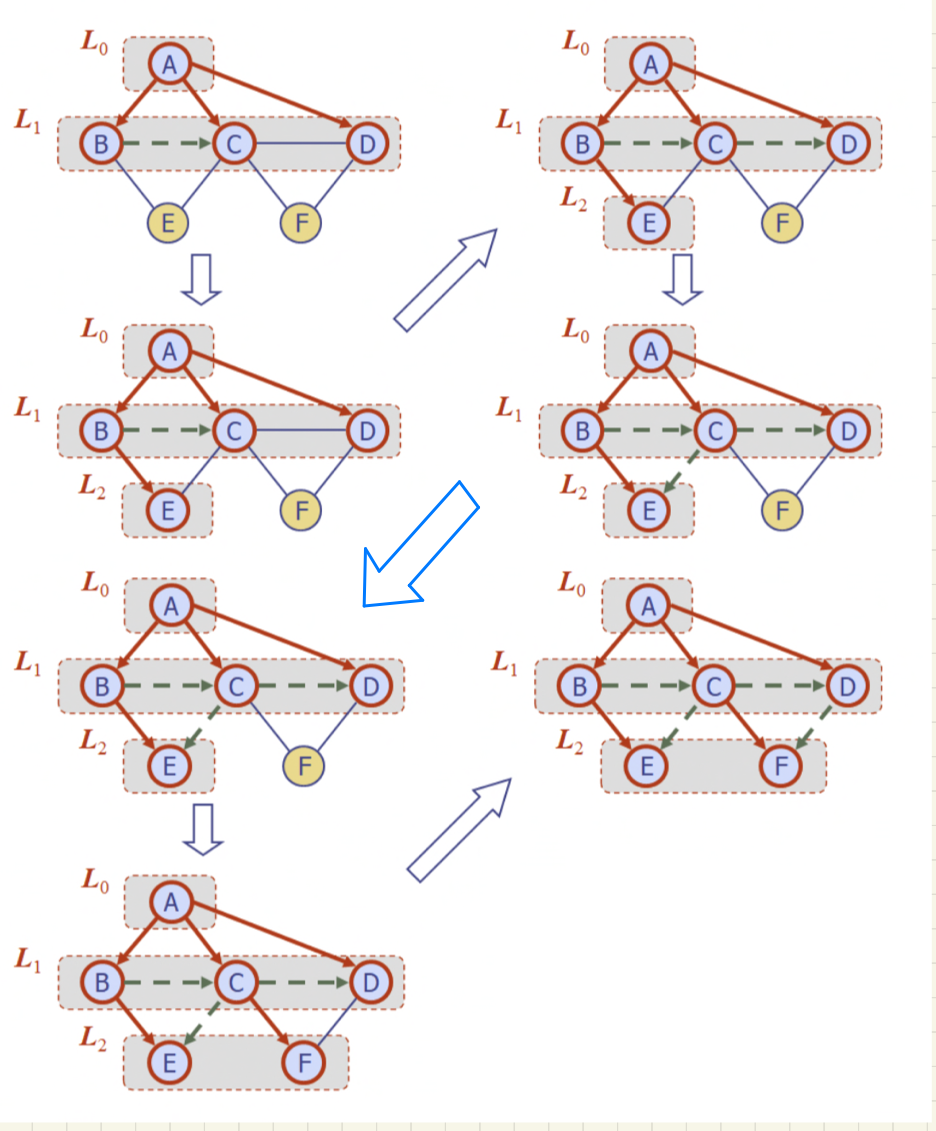
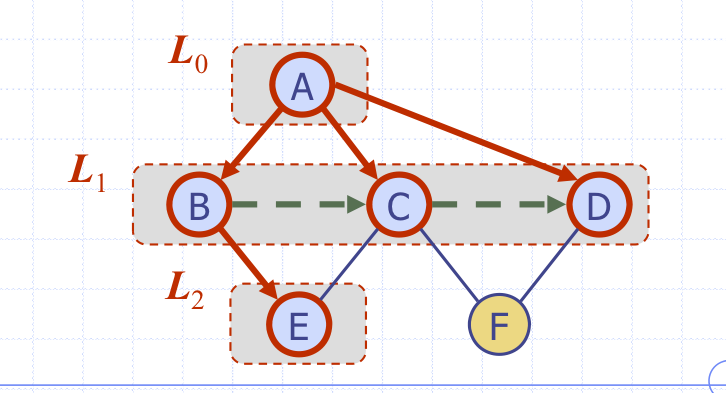
Properties

1. BFS(G,s)알고리즘은 모든 정점과 간선을 방문한다.
2. cross를 무시하면 discovery edges는 spanning tree를 형성한다.
3. 시퀀스 $L_i$의 각 정점들에 대하여

• s를 기준으로 v로 가려면 i번째 edge가 있다.
  (아래 그림에서는 A->E는 $L_0$ -> $L_2$까지 i = 2
• s부터 v까지 가는 path의 가장 짧은 거리는 i와 동일하다.
  

---

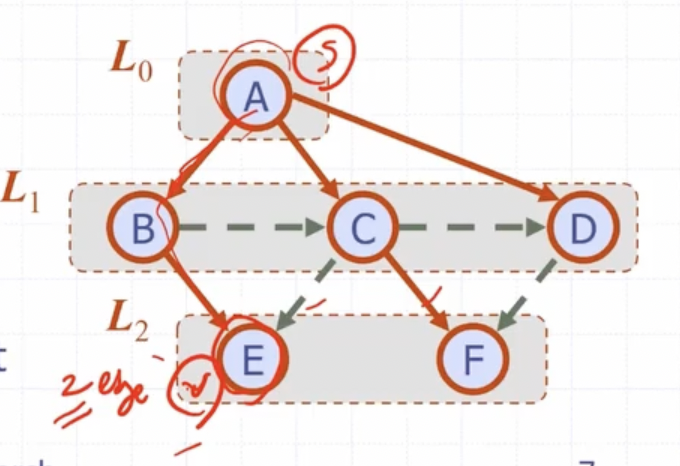
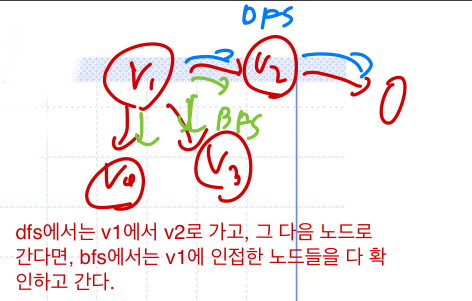
DSF vs BSF

공통점

• 그래프의 정점의 갯수가 n 이고 간선의 갯수가 m 일때, 인접리스트로 구현되면 O(n+m) 시간에 거쳐 수행된다. 이때, DFS와 BSF모두 한 정점당 deg(v) 만큼의 연산을 수행하므로,
  $ΣO(1)+O(deg(v)) = O(n) + O(2m) = O(n+m)$
• DFS(G,s)와 BFS(G,s)는 모두 s의 connected component의 모든 정점과 간선을 방문한다.
• discovery 간선 + 정점은 connected component의 spanning tree 중 하나이다.
• 모든 정점, 간선은 2번씩 레이블 된다.
  정점 : UNEXPLORED → VISITED
  간선 : UNEXPLORED → DISCOVERY or BACK ,CROSS

차이점

• BFS에서는 가장짧은 paths를 찾을 수 있다.
  

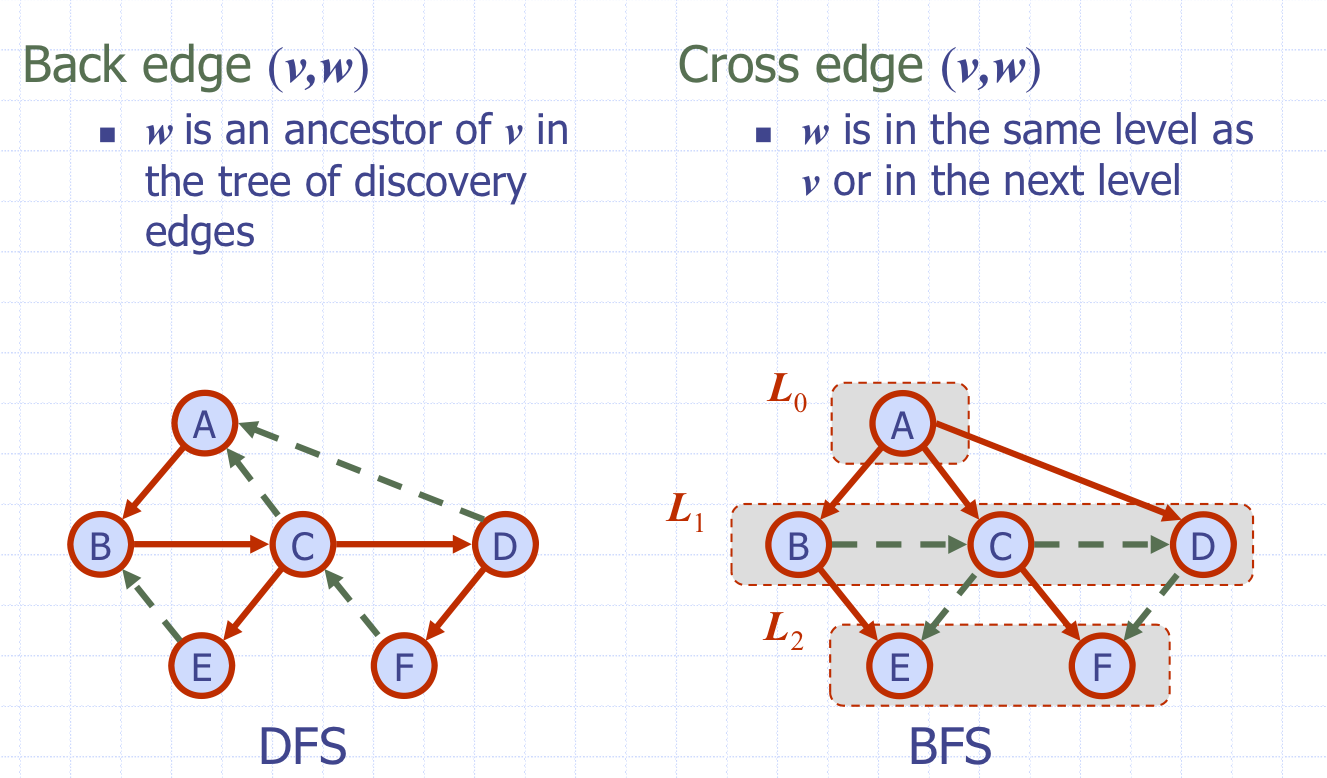
• BFS (Back edge(v,w))
  A => v, C => w라 한다면, w는 v의 조상이다.

• DFS (Cross edge(v,w))
  w는 v와 같은 레벨이거나 다음 레벨이다.
  (즉, 위의 레벨은 형성 불가)