DFS

용어정리

DFS를 배우기 앞서 먼저 몇가지 용어정리를 하고 들어가자.
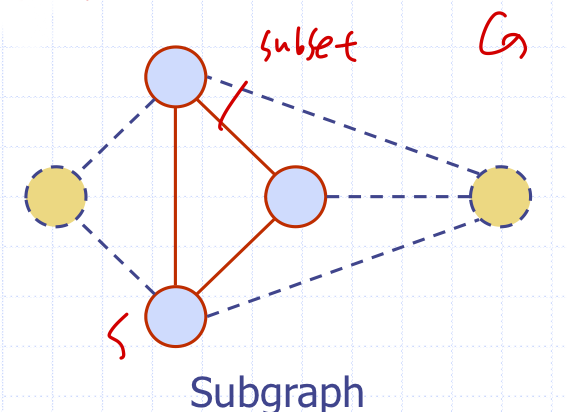
Subgraph
-> S의 정점들이 G의 정점들의 서브SET이고, S의 간선들이 G의 간선들의 서브SET이면 S가 G의 subgraph이다.

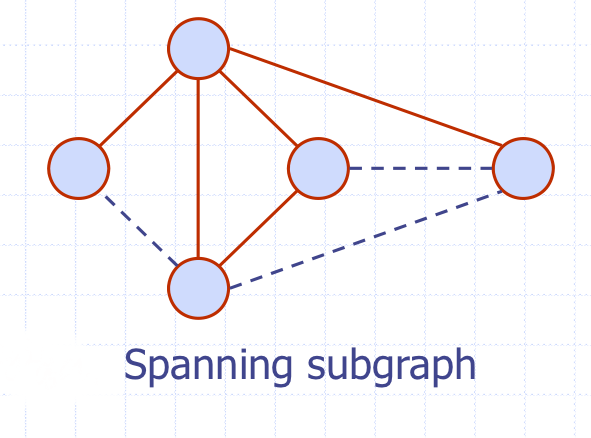
Spanning subgraph
-> 원래 그래프의 모든 정점을 포함하는 서브그래프를
신장그래프(spanning subgraph) 라고 한다.
(모든 간선은 포함하지 않아도 된다.)

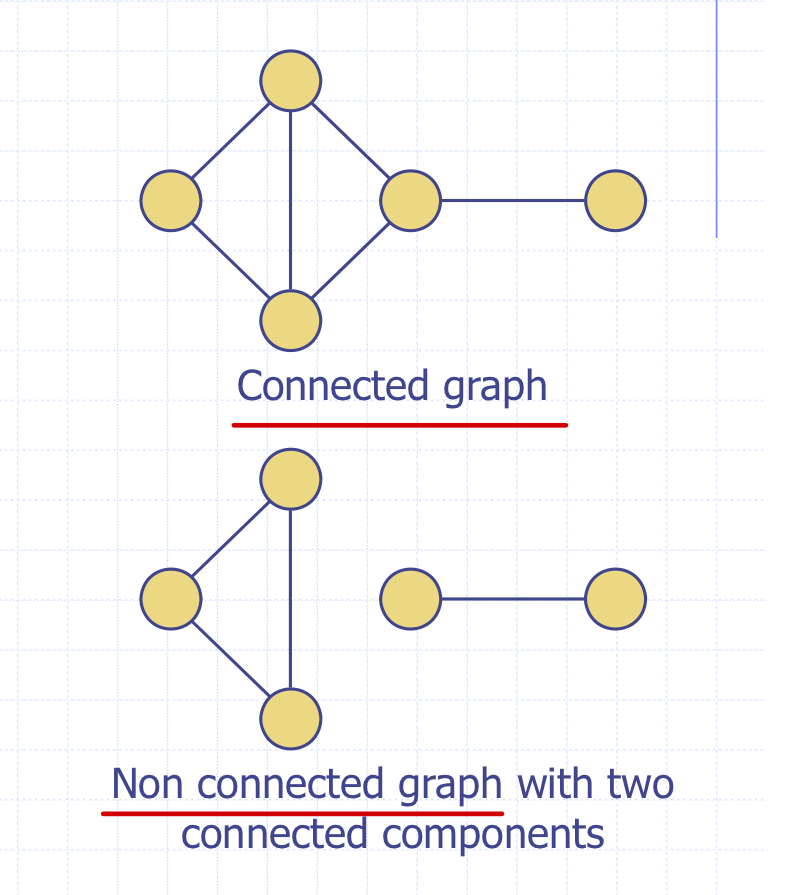
Connected graph
-> 모든 정점이 간선으로 연결되어있는 그래프.

Connected component
-> 연결된 subgraph중 가장 큰 단위.

Non connected graph
-> 말그대로 연결되어 있지 않은 부분이 있는 그래프

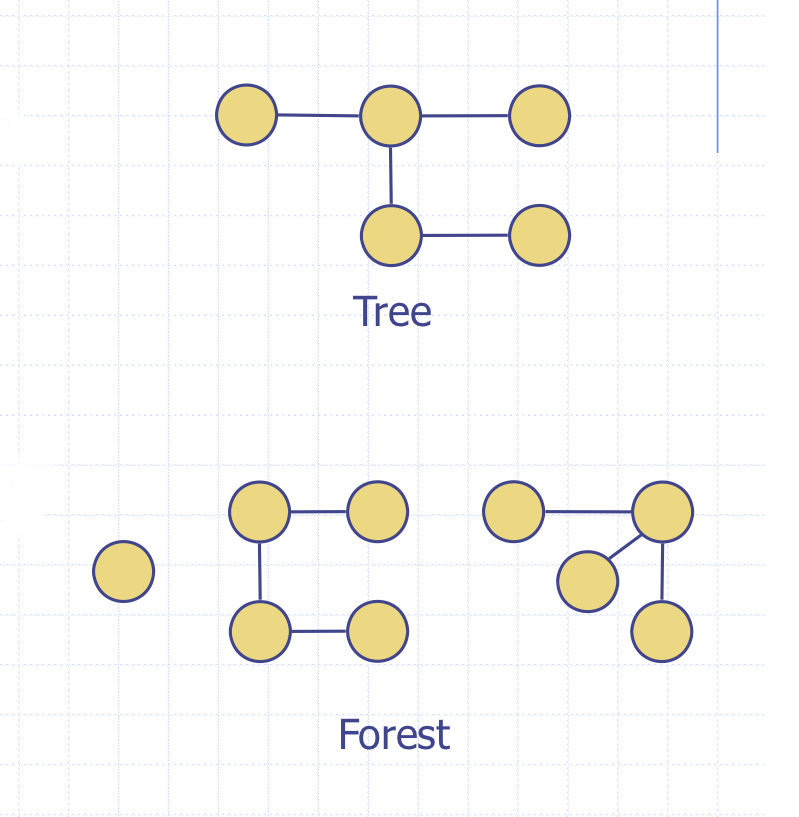
Tree
그래프가 cycle이 없는 connected graph.
앞에서 공부한 rooted트리와는 다르다.
->즉, 루트를 자유롭게 성정할 수 있다.

Forests
트리의 집합

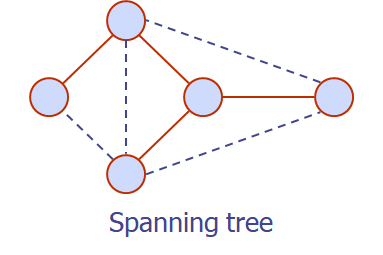
Spanning tree
connected graph의 spanning subgraph가 tree의 조건을 만족하면 Spanning tree라고 한다.
원래 그래프가 tree가 아니라면 spanning tree가 유일할 필요는 없다.

Spanning forest
spanning tree의 집합

---

DFS(Depth-First Search)란?

-> 깊이 우선 탐색
DFS는 그래프를 순회하는 알고리즘이다.

• 모든 정점과 간선들을 방문한다.
• G가 conneted인지 아닌지 판단한다.
• G의 연결된 components를 계산하거나 G의 spnning forest를 계산할 때 사용.(?)

DFS알고리즘

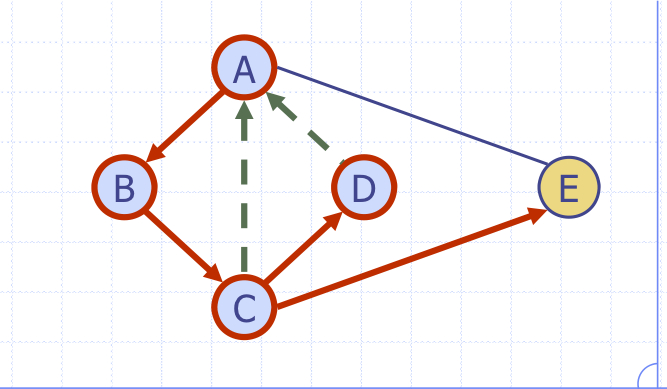
DFS알고리즘에서는 정점과 간선의 방문상태를 점검하기 위해 "label"이라는 개념은 도입한다.

• 정점
  -> unexplored: 방문되지 않은 초기 상태
  -> visited: 방문된 상태
• 간선
  -> unexplored: 방문되지 않은 초기 상태
  -> Discovery: 방문된 상태
  -> Back: 정점이 방문된 상태로 가려할 때

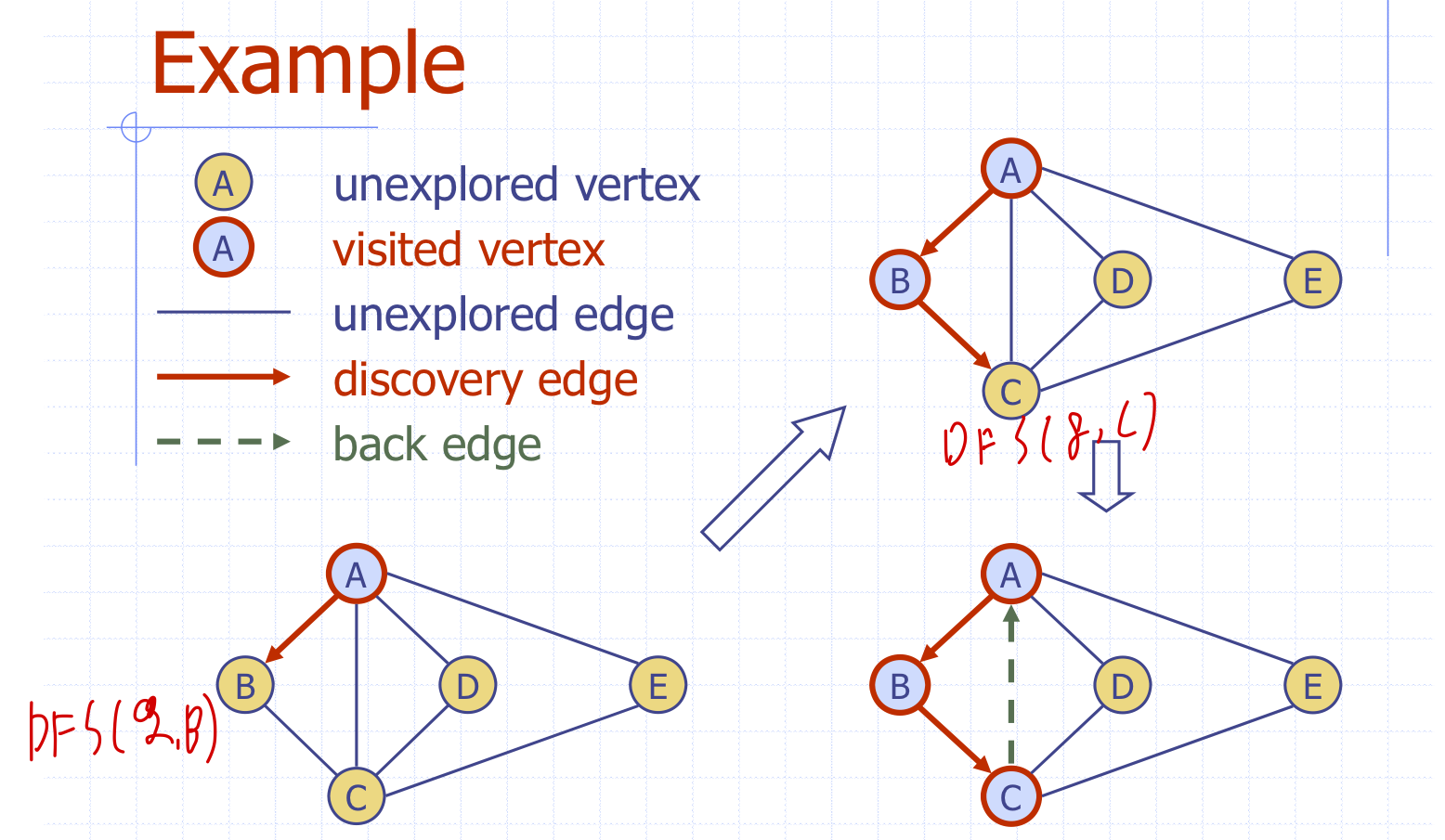
(좌) DFS(G)
-> $~~$ {v,e}입력으로 그래프 G를 삽입한 후, 정점과 간선들을 모두 초기상태로 초기화한다.

(우) DFS(G,v)

-> v의 label을 VISITED로 변경.
-> v와 연결된 간선이 UNEXPLORED인지 조사
-> UNEXPLORED이면 opposite(v)로 또 다른 정점을 w로 설정.
-> w가 UNEXPLORED인지 확인.
-> UNEXPLORED라면 해당 간선의 상태를 DISCOVERY로 바꾸고 DFS(G,w)수행
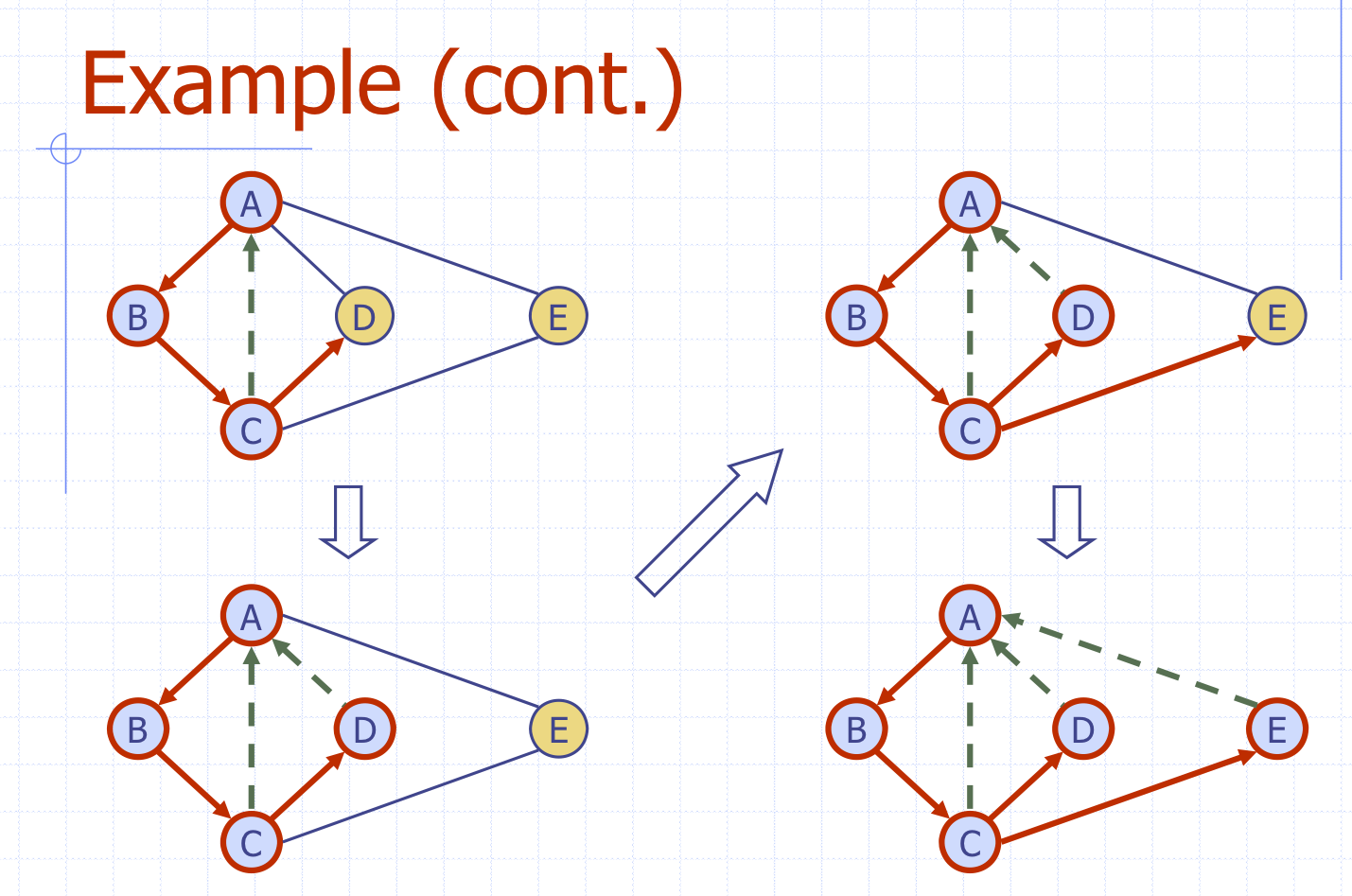
-> UNEXPLORED가 아닐 경우, 해당 간선의 상태를 BACK으로 변경.

예시

Properties

1) DFS(G,v)는 모든 connected component(정점, edge)를 방문한다.
2) 레이블된 discovery edge들은 v의 connected component의 spanning tree를 형성한다.

-> DFS의 시간복잡도는 O(n+m)이다. => 모든 정점과 간선들을 방문하기 때문.
-> 다음 장에서 공부하겠지만, DFS는 다음 분기로 넘어가기 전에 해당분기를 끝까지 탐색하고 넘어간다.
BFS는 시작 정점의 incident한 모든 부분들부터 탐색.