Hash Table

seonghun park·2022년 6월 3일

Hash Table

해시 테이블 or 해싱은 링크드 리스트로 구현된 딕셔너리이다.

해시 테이블은 해시 함수와 크기가 N 인 배열로 구성된다.

hash function => 주어진 키를 정수로 바꾸어 배열의 인덱스로 사용. (정수의 범위: 0 ~ N-1)
hash value(해시 값) => h(x) = x mod N (N = 배열의 크기)

hash table을 쓰는 목적

- 해시 테이블 : 해시테이블은 데이터의 해시 값을 테이블 내의 주소로 이용하는 궁극의 탐색 알고리즘이다. 빠르다고 정평이 나있는 이진 탐색보다도 빠르다.
- 암호화 : 해시는 입력받은 데이터를 완전히 새로운 모습의 데이터로 만든다. SHA(Secure Hash Algorithm)알고리즘이 그 대표적인 예이다.
- 데이터 축약 : 해시는 길이가 서로 다른 입력 데이터에 대해 일정한 길이의 출력을 만들 수 있다. 이 특성을 이용하면 커다란 데이터를 '해시'하면 짧은 길이로 축약할 수 있다. 이렇게 축약된 데이터끼리 비교를 수행하면 커다란 원본 데이터들을 비교하는 것에 비해 엄청난 효율을 거둘 수 있다.

Hash function

앞에서 본 예시 이외에 k가 정수가 아닌 경우가 발생할 수 있다.

이러한 경우를 대비하여 일반적인 해시함수는 2단계를 준비한다.

Hash code : key를 정수 i 로 변환
Compression function : 정수 i 를 [0,N-1] 에 해당하는 값으로 변환

1단계를 $h_1(k)$ , 2단계를 $h_2(i)$ 라고 할때,

해시함수는 합성함수 $h(k) = h_2((h_1(k))$ 로 표현된다.

Hash function

해시 함수는 두가지 과정을 거친다.

h1: Hash code => 키를 정수로 바꿔준다.
h2: Compression function => 정수를 [0,n-1]에 해당되는 값으로 변환해준다.
이를 h(x) = h2(h1(x)), 합성함수로 표현할 수 있다.

Compression function에 대해 더 알아보자.

Division
$h_2(y) = y~ mod~ N$
주어진 정수 y를 0~N-1 사이로 변환하는 가장 기본적인 방법이다.
이때 배열크기 N을 소수로 설정하면 해시값과 N은 서로소이므로 (해시값 0,1 일때 제외) 더 분산되게 저장할 수 있다.
Multiply, Add, Divide (MAD)
$h_2(y)=(ay+b)~mod~N$
a를 곱하고 b를 더한 다음 N 으로 나머지 연산하는 방법이다.
마찬가지로 규칙성을 파괴하고 더 잘 분산시키기 위해 사용된다.
이 때, (a,b>0 && a%N!=0)

Collision Handling (충돌 관리)

Collision => 이미 차있는 자리에 값이 들어가려 하는 것.
이러한 충돌을 해결하는 방법에 따라 해시 테이블의 종류가 달라진다.

Separate Chaining

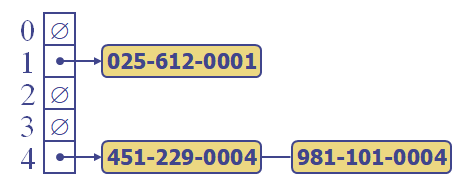
같은 해시값을 갖는 원소들을 시퀀스로 묶고, 해시 테이블에는 해당 시퀀스의 주소를 저장한다.
(추가적인 공간을 할당해서 값을 넣어주는 것)
(각 셀마다 Linked-List가 있다고 생각.)

단점 - 간단하지만, 추가적인 메모리를 필요로 한다.

Open addressing
아이템들이 각기 다른 셀에 들어가있는 것
즉, 충돌된 아이템들의 데이터를 다른 주소에 저장할 수 있게 한다.
이 때 충돌을 다루는 방식으로 Linear probing과 Double hashing이 있다.
Linear probing
충돌을 다루는 방식.
예를 들어 해시 함수를 통해 셀에 삽입하다가 충돌이 일어났다고 가정해보자.
우선 충돌이 일어난 셀의 다음 위치로 옮겨간다.
옮겨간 위치가 비어있다면 그 위치에 아이템을 넣는다.
**Double Hashing
선형 탐사에서는 데이터가 고루 분포되지 않고 뭉치며, 그럴수록 많이 이동해야 하기에 오랜 시간이 걸린다는 단점이 있다.
이를 해결할 것이 더블해싱이다.(즉, 널리 퍼뜨리기)
이중해싱은 아래 2개의 해시함수를 이용한다.
h(k) = k mod N
h`(k) = q - (k mod q)
테이블 사이즈 N은 소수여야 한다.
q는 임의로 정해주는 값이며 소수를 이용한다.
q < N