Graph

Graph란?

그래프는 정점과 간선(V, E)을 저장하는 자료구조이다.

Edge(간선) Types

-Directed graph
방향을 갖는 Directed edge로 이루어진 그래프
출발하는 정점 u를 origin 이라 하고 도착하는 정점 v를 destination 이라 한다.
(u,v) != (v,u)

• Undirected graph
  방향을 갖지 않는 Undirected edge로 이루어진 그래프이다.
  (u,v) == (v,u)

---

용어정리

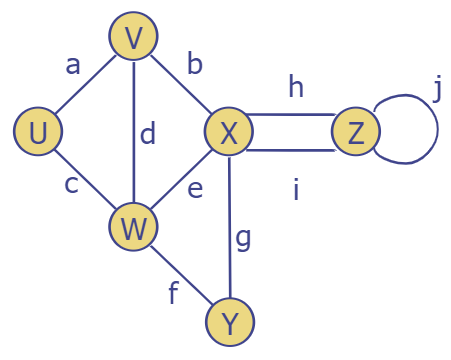
• End Vertices(endpoints) - 간선의 양 끝 정점
  -> U와 V는 a의 endpoint이다.

• incident - 정점에 연결된 간선들의 관계
  -> 정점 V의 incident edges는 a,d,b 이다.

• adjacent - 간선으로 이어진 두 정점 사이의 관계
  -> 정점 U와 V는 adjacent.(인접하다.)

• degree - 한 정점에 연결된 간선의수
  -> X의 degree는 5이다.

• parallel edges - 간선들이 같은 endpoints를 가질 때.
  -> 간선 h와 i는 parallel edges이다.

• self-loop - 양 끝이 하나의 정점에만 연결된 간선
  -> 간선 j 는 self-loop다.
  

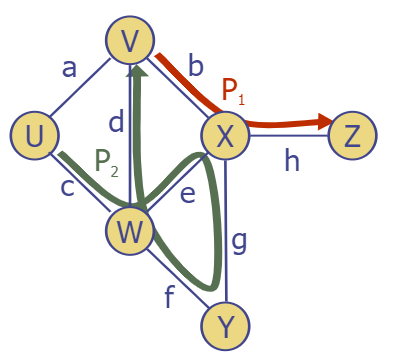
• Path - 경로
  ex. P1 = (V, b, X, h, Z) or (V, X, Z)
  ex. P2 = (U, c, W, e, X, g, Y, f, W, d, V) or (U, W, X, Y, W, V)

  Simple graph일 때는 간선을 생략하고 표현할 수 있다.
  Simple graph => pallele edge, self loof가 없은 그래프

• Simple Path (단순경로) - 중복하여 방문하는 정점, 간선이 없는 경로
  -> P1 = simple path
  -> P2 = not simple path

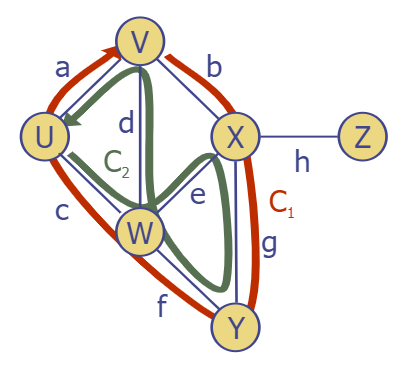
• Cycle - 시작 정점과 도착 정점이 동일.
• Simple Cycle - 중복하여 방문하는 정점, 간선이 없는 사이클
  -> C1 = simple cycle
  -> C2 = not simple cycle

---

Properties (undirected의 경우)

---

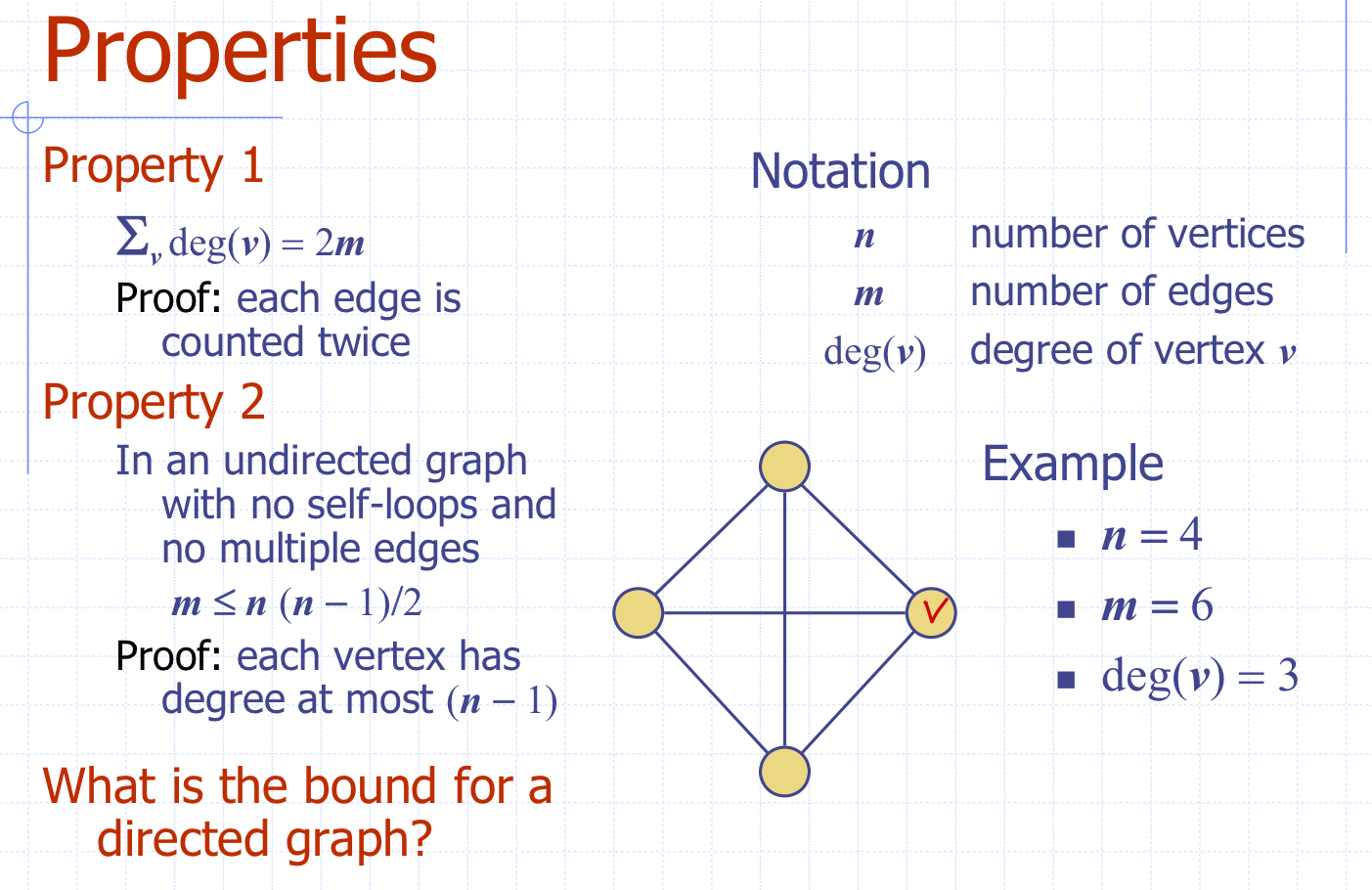
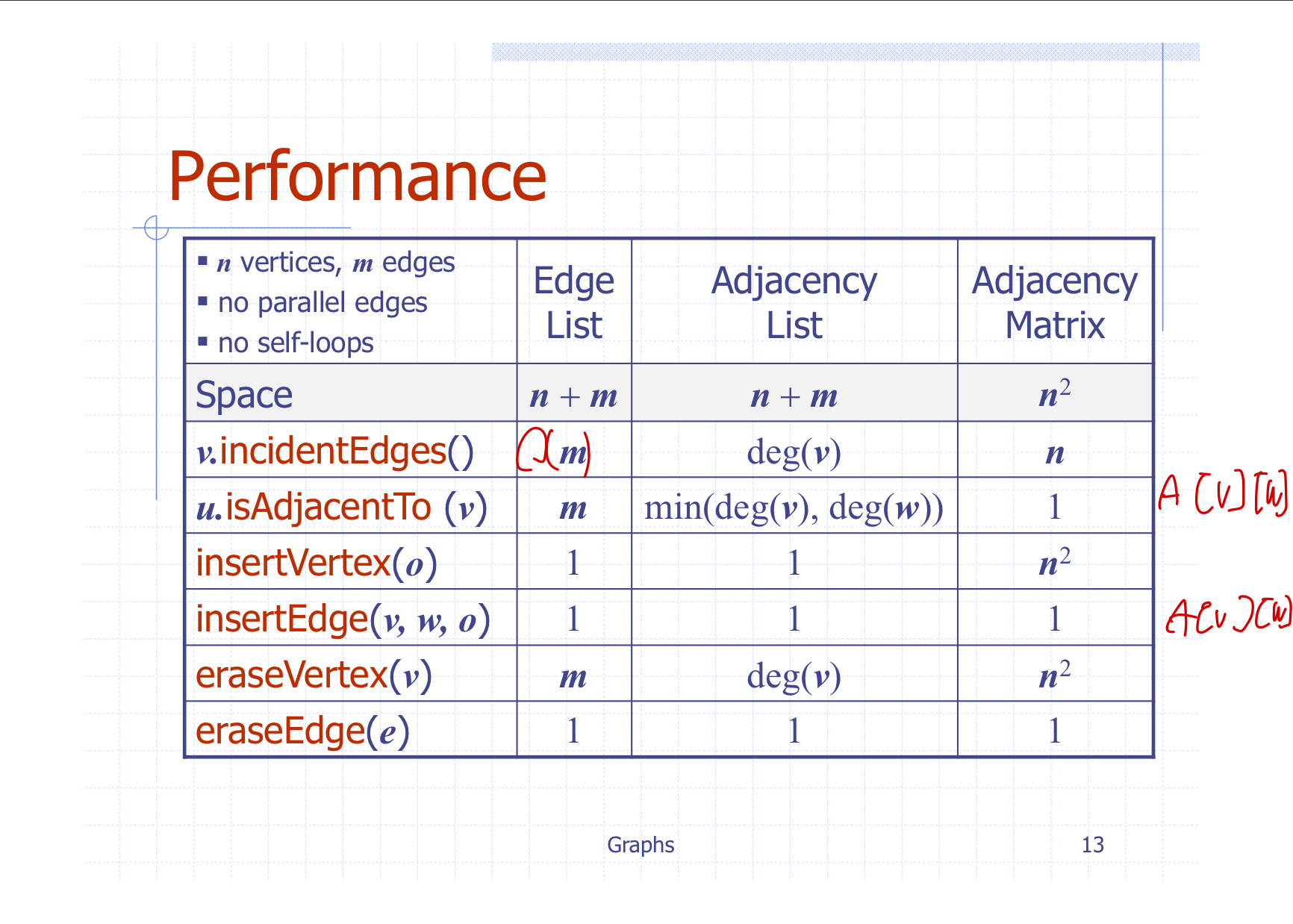
Graph ADT

Vertices and edges

• are positions
• store elements

Accesor methods

• e.endVertices()
  간선 e의 양 끝 정점을 리스트 형식으로 리턴
• e.opposite(v)
  간선 e의 정점 v이외에 또 다른 정점을 리턴
• u.isAdjacentTo(v)
  정점 u와 v가 인접해있는지를 boolean으로 리턴

Update methods

• insertVertex(o)
  o 라는 데이터를 저장하는 정점을 추가
• insertEdge(v,w,o)
  정점 v,w 를 연결하면서 데이터 o를 갖는 간선을 추가
• eraseVertex(v)
  정점 v와 그것과 연결된 모든 간선을 삭제
• eraseEdges(e)
  간선 e를 삭제

Iterable collection methods

• neighbors(v)
  정점 v 와 인접한 정점들을 리스트 형식으로 리턴
• vertices(), edges()
  그래프의 모든 정점, 간선을 리스트 형식으로 리턴

---

그래프 구현

Edge List Structure

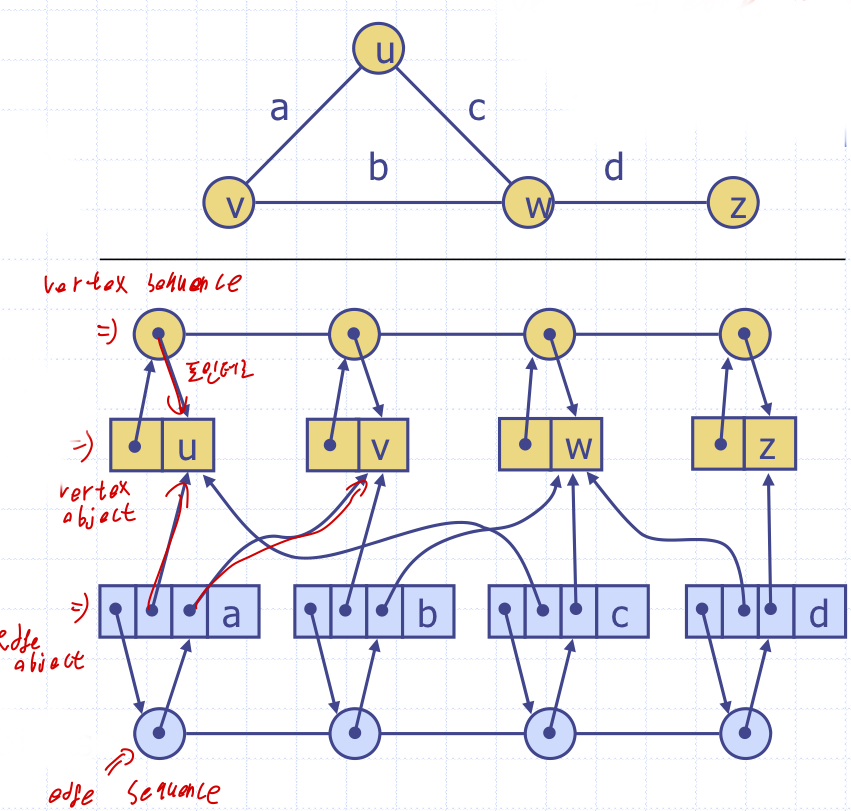
그래프 구현의 가장 기본적인 구조

• Vertex sequence
• Edge sequence
  -> 시퀀스는 내부에 노드의 position을 저장한다.
• Vertex object
  - element
  • vertex 시퀀스 안에 position의 주소.
• Edge object
  - element
  • Edge 시퀀스 안에 position의 주소.
  • origin 정점의 주소
  • destination 정점의 주소

단점 임의의 노드 Incident Edge를 찾을 때 처음부터 탐색해야 한다. 그 이유는 edge->vertex로의 연결은 있지만, vertex->edge로의 연결이 없기 때문
따라서 O(m)이 걸린다.

---

Adjacency List Structure

• Edge List Structure기반
• Incidence sequence for each vertex
  - 정점과 연결된 간선들의 position을 저장하고 관리하는 시퀀스
  -> vertex object에 링크를 추가해서 incidence 시퀀스를 가리키게 한다.
  

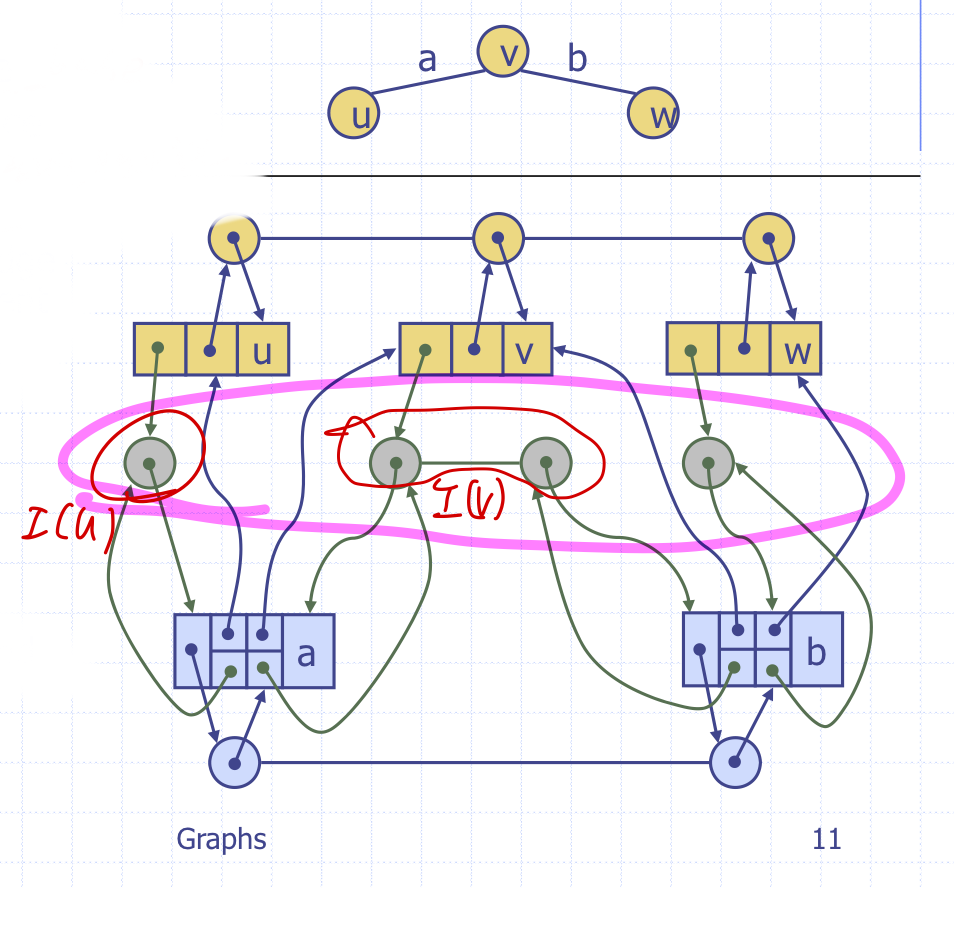
  간선에 대한 연산을 O(m)에서 O(deg(v))로 줄여준다.

---

Adjacency Matrix Structure

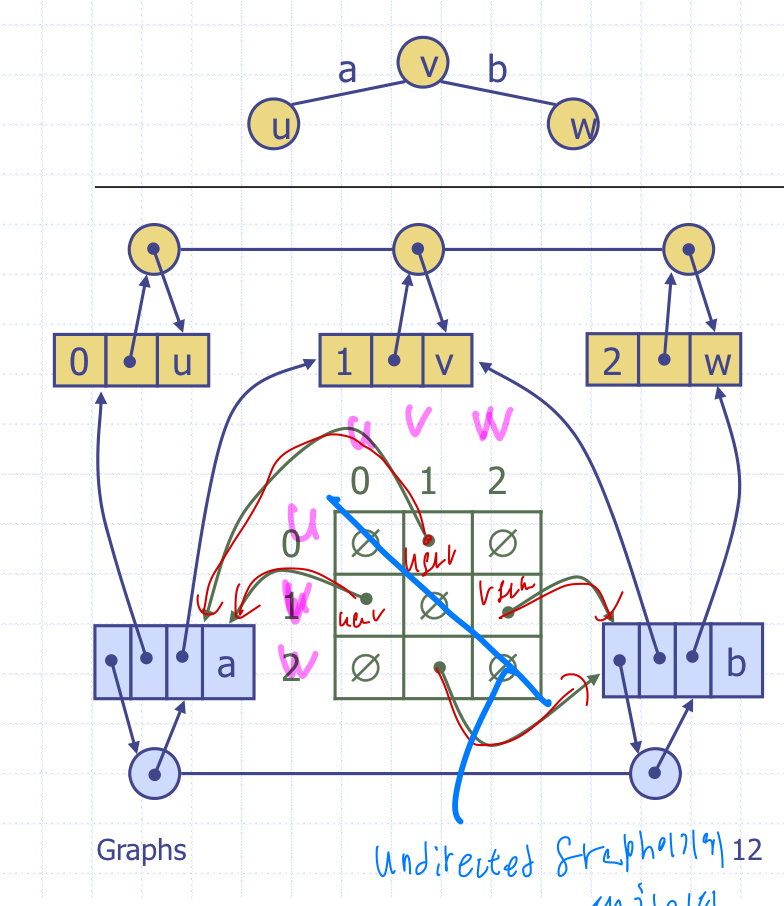
• Edge List Structure기반
• Vertex Object의 구조
  필드가 추가되어 0~n-1 의 정수를 저장한다.
• 2D-array adjacency array
  크기가 n*n인 행렬이 존재
  i 행 j 열에는 i 번째 정점과 j 번째 정점의 연결 정보에 대해 저장한다.
  ⇒ 연결되었으면 연결해주는 간선의 주소를, 연결되어있지 않으면 NULL값을 저장

undurected graph이기에 대칭구조를 이룬다.

---