우선순위큐란 무엇일까?
지금까지 배운 자료구조에서는 우선순위가 따로 없었다. 예를 들어 일반적인 큐는 선입선출 구조로 키에 대한 별다른 우선순위가 없었다.
우선순위 큐는 말 그대로 각 entry들이 "우선순위"에 따라 정렬된 큐를 말한다.
-> unsorted sequence, sorted sequence, heap으로 구현할 수 있다.
Priority Queue ADT
-
PQ에는 (key, value)로 구성된 entry가 저장된다. 여기서 key가 우선순위를 나타낸다.
-
Main methods
-> insert(e) : entry e를 삽입
-> removeMin(): 가장 작은키 삭제(우선순위가 높다는 뜻) -
부가메소드
-> min: 최솟값 반환, 삭제는 안함.
-> size(), empty()
PQ Sorting
Comparator ADT
-> PQ Sorting에 앞서서 Comparator 클래스에 대해서 알아보자.
Comparator는 두 값을 비교해주는 클래스로 isLess(p,q){ p<q이면 true}
PQ Sorting
- input -> list S, comparator C
- output -> C에 따라 정렬된 list S, PQ
sort하는 방법은 어렵지않다.
1. S가 빌 때까지 맨 앞을 지우고, P에 삽입한다.
2. P의 최솟값을 다시 S의 tail에 삽입한다.
이때, 시퀀스에서 삽입, 삭제는 O(n)에 이뤄지므로 P의 삽입과 삭제 수행시간에 따라 시간복잡도가 달라진다.
List기반 PQ
list의 상태에 따라 삽입과 삭제의 시간복잡도가 달라진다.

-
unsorted list
insert -> O(1)
삽입은 순서상관없이 대충
removeMin, min -> O(n)
최솟값 찾는 연산 최악으로 n번 -
sorted list
insert -> O(n)
정렬되어야 하기에 삽입을 신중히
removeMin, min -> O(1)
최솟값은 맨 앞
PQ-sort의 변형인 두 가지 알고리즘을 알아보자.
1. Selection-Sort(선택정렬) - unsorted list로 구현된 PQ
-
insert - S가 빌 때까지 S 요소를 우선순위 큐 P에 삽입
insert(O(1)) 를 n번 반복 → O(n) -
removeMin - P가 빌 때까지 P의 가장 작은 값을 S에 차례로 삽입
비교연산(O(n))을 하는 min, removeMin 을 n번 반복 → n + ... + 2 + 1 → n(n+1)/2 → O(n^2)

PQ에 삽입과정은 맨 앞부터, 정렬할 때 우선순위대로.
2. Insertion-Sort(삽입정렬) - sorted list로 구현된 PQ
-
insert - S가 빌 때까지 S 요소를 우선순위 큐 P에 삽입
비교연산을 하는 insert 를 n번 반복 → 1 + 2 + ... + n → n(n+1)/2 → O(n^2) -
removeMin - P가 빌 때까지 P의 가장 작은 값을 S에 차례로 삽입
min, removeMin 을 n번 반복 → O(n)

PQ에 삽입과정은 맨 앞부터, 정렬할 때 우선순위대로.
In-place sort (제자리정렬)
blue: Priority Queue
yellow: Sequence
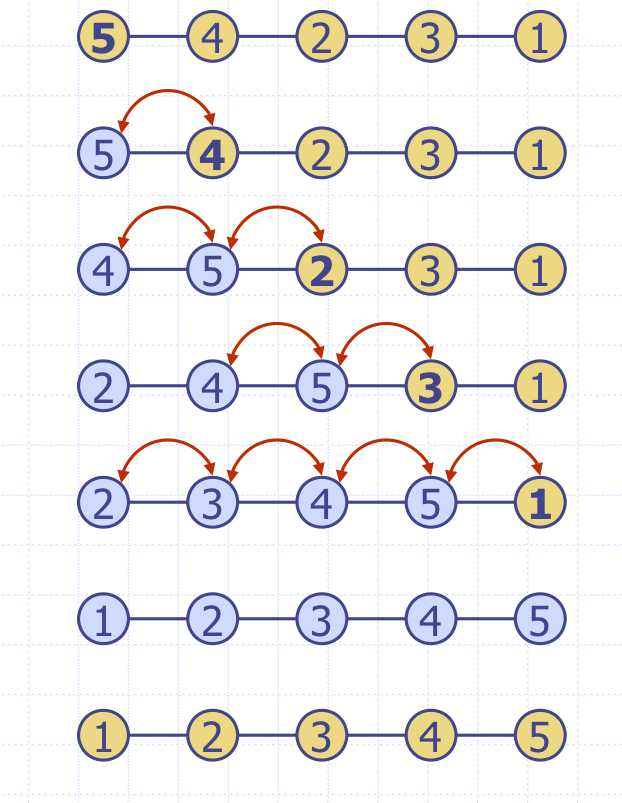
새로운 데이터구조를 만들지 않고, swaps을 통해 그 자리에서 insertion-sort를 구현한다.
이 역시 시간복잡도는 O(n^2)
