Heap은 무엇일까?
힙은 array, list를 이용하여 구현 가능한 자료구조로 binary tree의 일종이다.
-> 힙을 이용하여 PQ의 단점을 극복할 수 있다.(시간복잡도 문제 해결)
힙은 다음과 같은 두 조건을 선행해야 한다.
1. Heap_Order
루트노드를 제외한 모든 internal노드 v는 key(v)>=key(parent(v))를 만족한다.(자식노드의 key가 더 크다.)
2. Complete Binary Tree
완전 이진트리 구조여야 한다.
- 깊이 i(0 <= i <= h-1)에는 최대 2^i개의 노드가 있다.
- 깊이 h-1에서 internal노드는 external노드의 왼쪽에 있다.
- last node는 마지막 레벨의 가장 오른쪽에 있는 노드이다.
완전 이진 트리 Complete binary tree
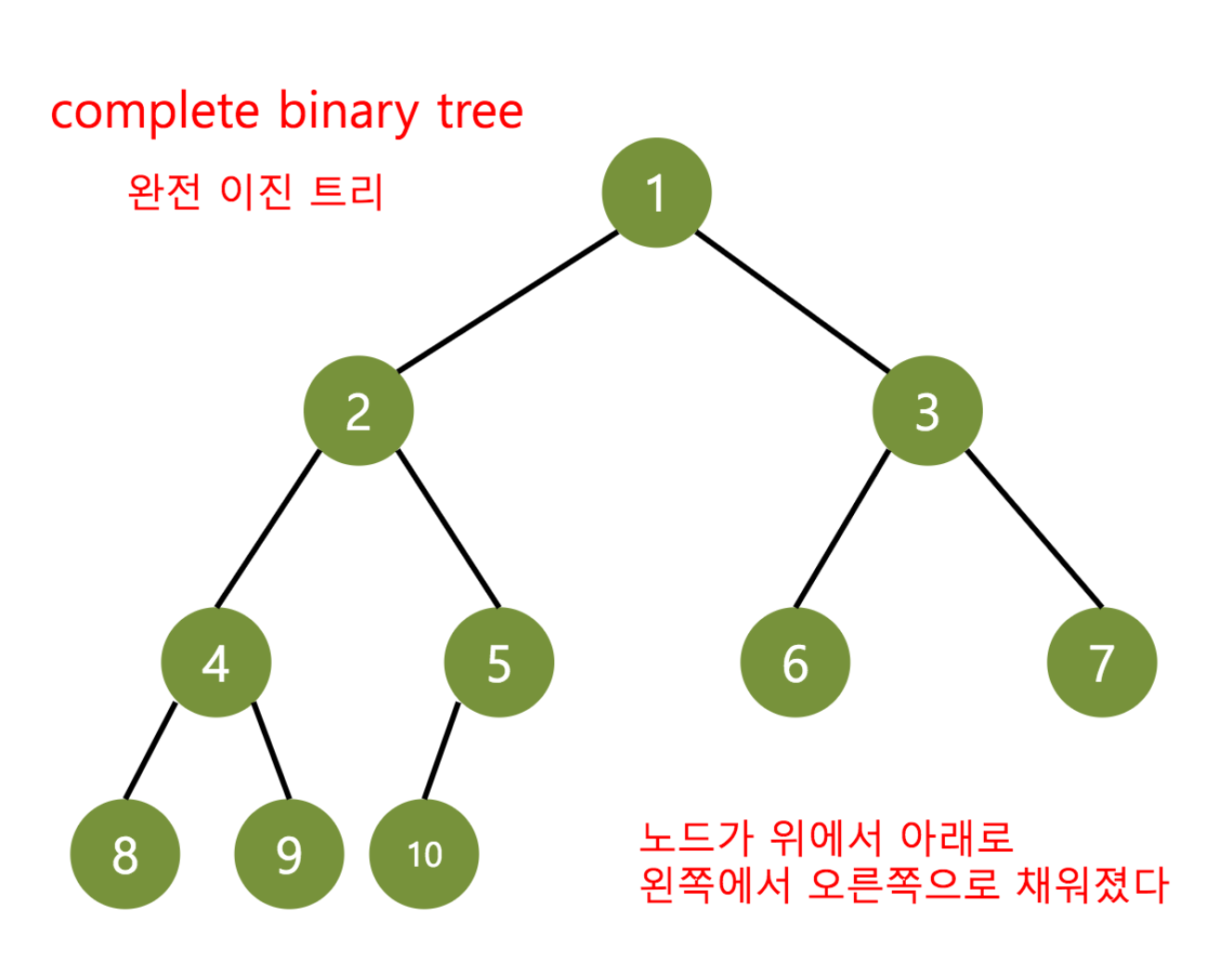
마지막 레벨을 제외하고 모든 노드가 가득 차 있고, 마지막 레벨의 노드는 왼쪽으로 몰려 있어야 한다.
Height of a Heap
n 키를 저장하는 힙의 height 는 O(log n)이다.
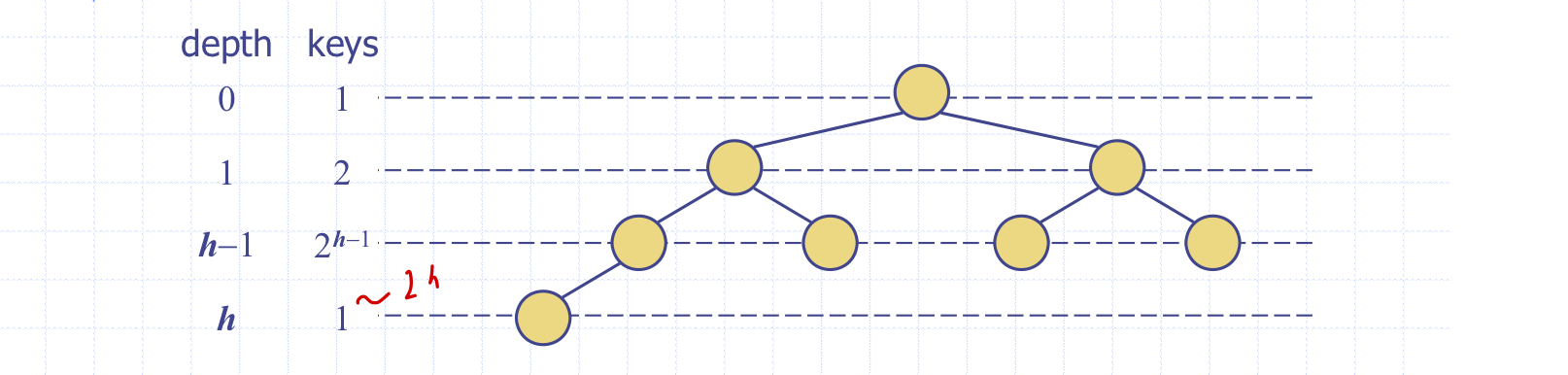
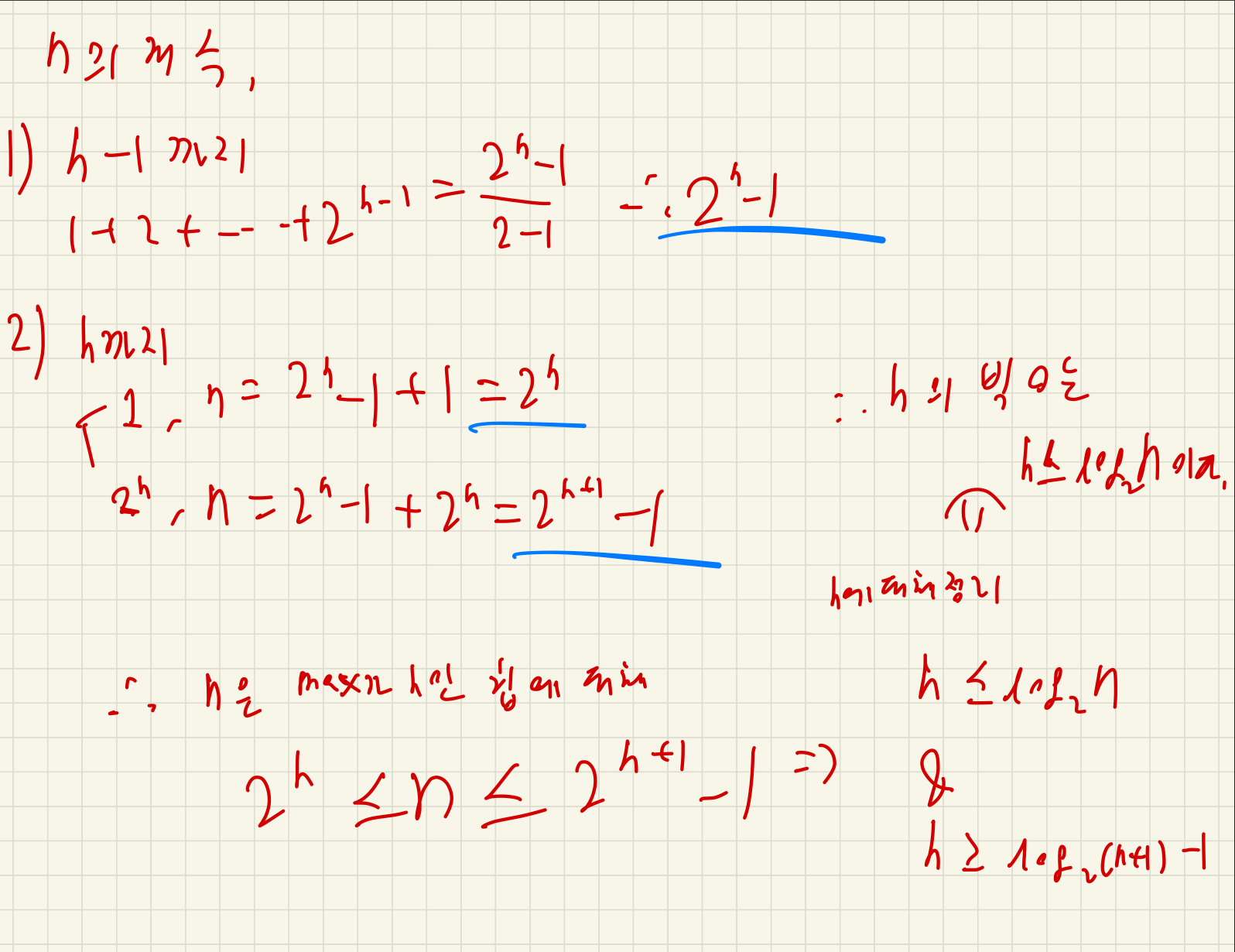
Heap을 이용하여 PQ를 구현해보자
Insertion
heap에 k를 삽입해보자.
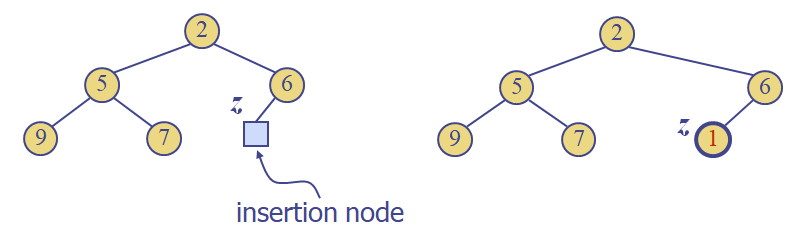
1. node z를 찾는다. O(1)
2. z에 k를 저장한다. O(1)
3. Heap-order를 위반하면 재배열한다. O(log n)
재배열의 과정 -> Upheap
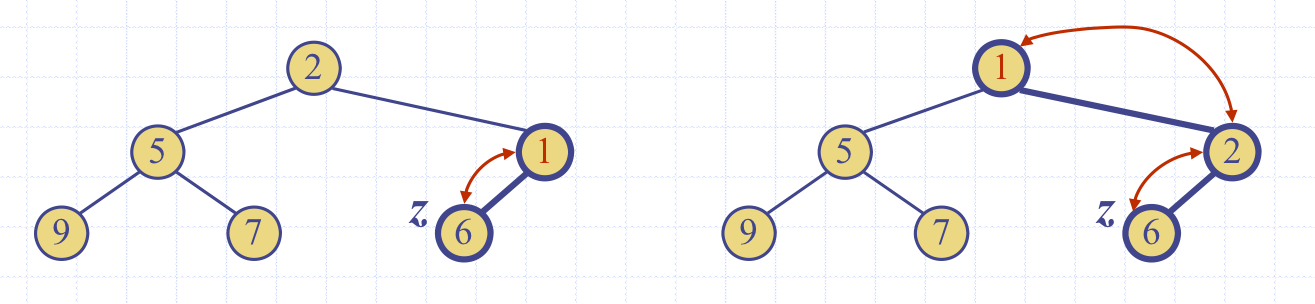
업힙은 스와핑과정을 통해 heap-order property를 만족하기 위한 수행을 한다.
Upheap은 key k가 루트에 도달하거나, 적당한 위치에 도달했을 때 종료된다.
Removal
removeMin
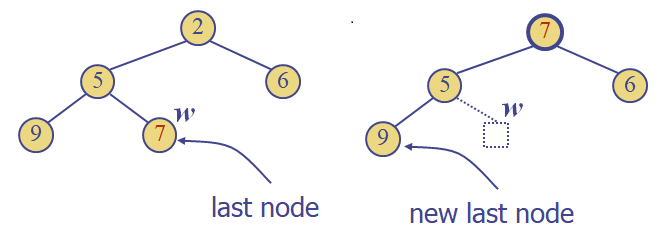
1. 루트노드에 최솟값이 저장되어 있으므로 last node w의 key와 root의 key를 교환
2. w제거(removeMin)
3. Heap-order를 위반하면 재배열한다. O(log n)
재배열의 과정 -> downheap
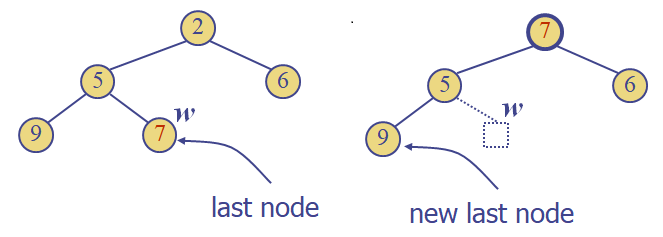
last node와 root노드의 키를 바꾸어주었기 때문에 downheap과정을 통해 heap-order를 재배열한다.
