[프로그래머스] 도넛과 막대 그래프(Java)

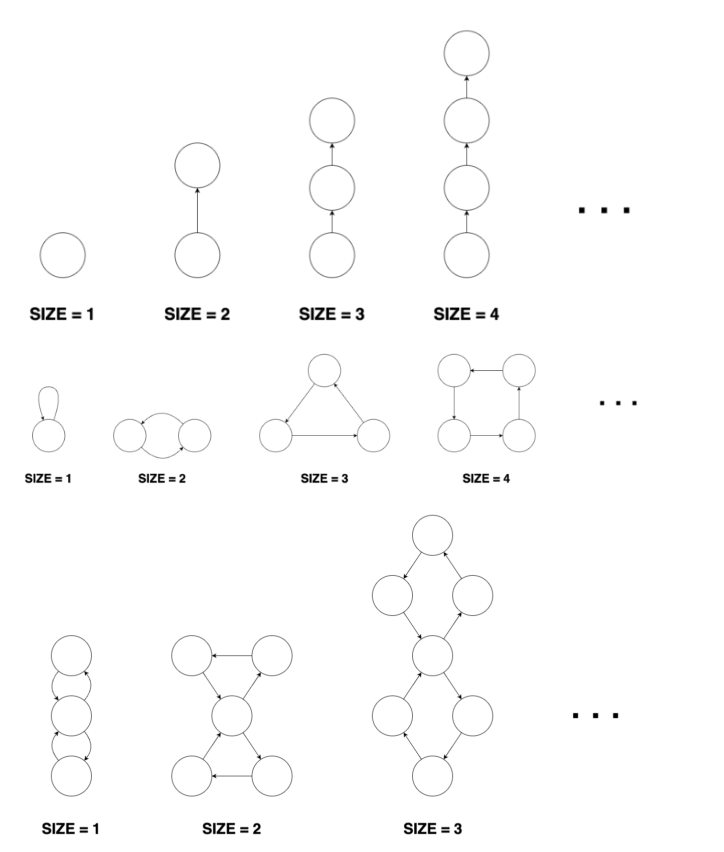
문제 설명

문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/258711

난이도: Level2

접근 방법:
이 문제는 세 가지 모양의 그래프와 생성된 정점의 특징을 분석하는 것이 핵심인 문제입니다.

문제의 핵심: 그래프를 각각 구별할 수 있는 고유의 특징을 찾아야 합니다.

1. 생성된 정점: 나가는 간선이 2개 이상 존재하고, 들어오는 간선이 존재하지 않습니다.
2. 막대 모양 그래프: 생성된 정점과 연결된 간선을 제외했을 때, 나가는 간선이 없는 정점이 하나 존재합니다. 나머지 정점들은 들어오는 정점과 나가는 간선이 모두 하나씩 존재합니다.
3. 도넛 모양 그래프: 생성된 정점과 연결된 간선을 제외했을 때, 모든 정점이 나가는 간선과 들어오는 간선이 하나씩 존재합니다.
4. 8자 모양 그래프: 생성도니 정점과 연결된 간선을 제외했을 때, 1개의 정점을 제외하면 나가는 간선과 들어오는 정점이 하나씩 존재합니다.
   1개의 정점은 나가는 간선 2개와, 들어오는 간선 2개가 존재합니다.

문제 풀이

1. 그래프를 초기화 한다.
2. 그래프를 순회하면서 생성된 정점을 찾는다. (나가는 간선이 2개 이상 존재하고, 들어오는 간선이 존재하지 않는 점)
3. 생성된 정점을 찾으면, 이와 연관된 간선들의 정보를 삭제한다.
   (생성된 정점과 연결 정보 삭제를 하여 그래프들을 고유의 모양으로 구분이 되게 끔 한다)
4. 막대 모양 그래프의 갯수를 찾는다.(나가는 간선이 없는 정점의 갯수)
5. 8자 모양 그래프의 갯수를 찾는다.(나가는 간선 2개, 들어오는 간선이 2개인 정점의 갯수)
6. 전체 그래프의 갯수에서 막대 모양 그래프의 갯수와 8자 모양 그래프의 갯수의 합을 빼면, 도넛 모양 그래프의 갯수를 구할 수 있다.
   전체 그래프의 갯수는 생성된 정점에서 연결된 간선의 수이다.!!

시행 착오

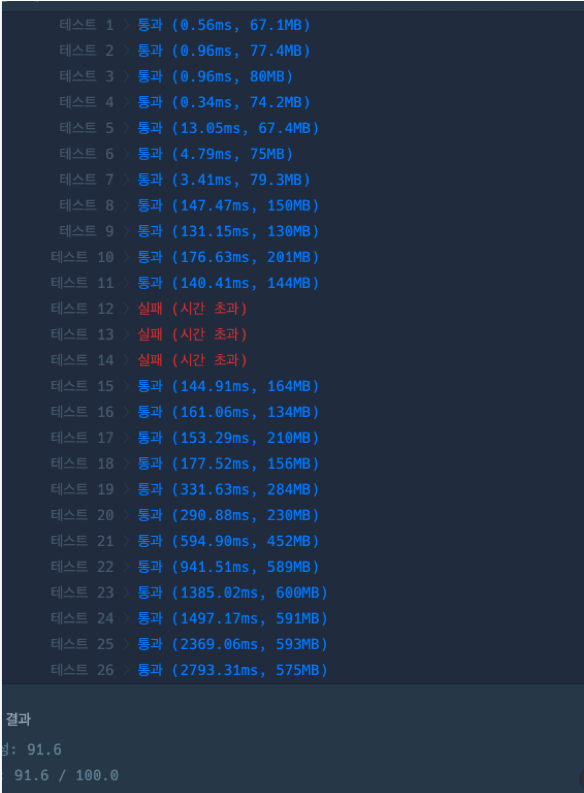
3개의 테스트 케이스가 시간 초과가 났다.

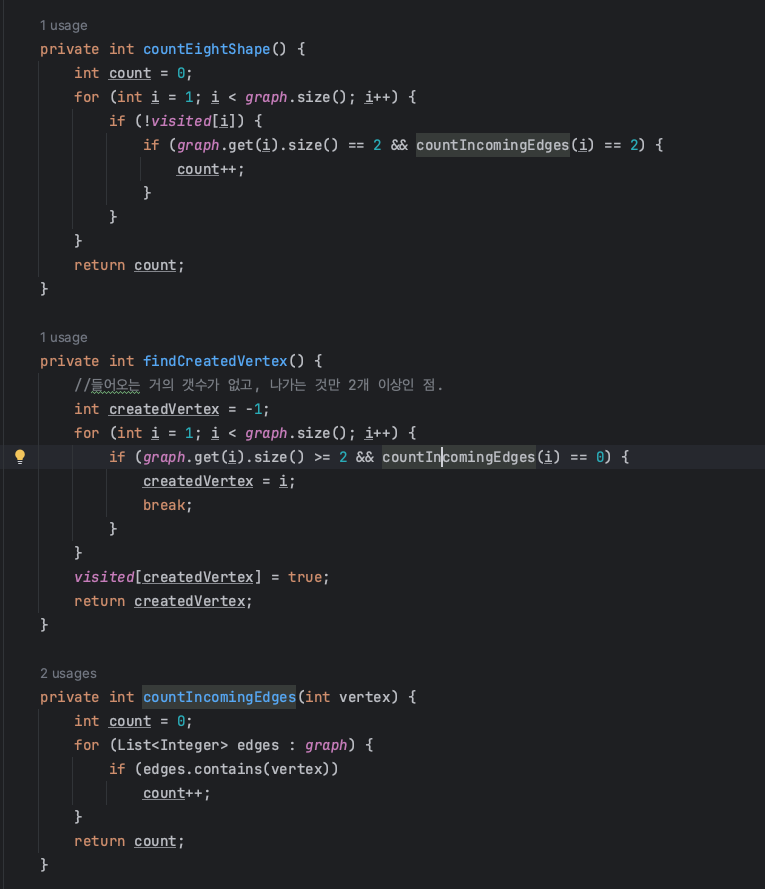
특정 vertex로 들어오는 간선의 수를 세는, countIncomingEdges를 이렇게 작성했었다. 그리고, 시작 정점을 찾는 메소드, 8자 모양 그래프의 수를 세는 메소드들에서 이 함수를 이용하는데 모든 정점에서 countIncommingEdges를 호출하다보니, 정점이 매우 많은 경우,
똑같은 정점에서 들어오는 간선의 수를 세는 countIncommingEdges를가 도넛 모양 그래프의 수, 8자 모양 그래프에서 중복되어 실행되는 비효율적인 구조였다.

그래서 아래와 같이 incommingEdges 배열을 만들어, index번째 vertex에 들어오는 간선의 수를 저장해두도록 바꾸고, 초기화를 했다.

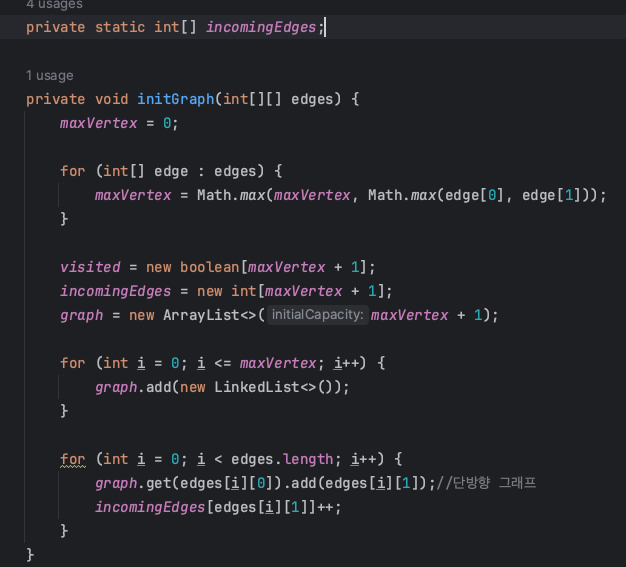
이렇게 수정을 하니,

테스트 케이스가 통과하였다.

깨달은 점

여러번 자주 이용하는 값은 계산해서, 배열로 저장해놓는 것이 매우 효율적이다. 여러 곳에서 똑같은 값을 계산하기 위해 계산하는 메소드를 호출하는 것은 매우 비효율적이라는 것을 깨달았다.

문제 후기

카카오 겨울 코테 인턴쉽에서 나왔던 문제다.
level2 치고 난이도도 꽤 있었던 문제 같았다.
그래프마다의 특징을 명확하게 파악하는게 중요했던 문제같다.

전체 코드

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

class Solution {

    private static List<List<Integer>> graph;

    private static boolean[] visited;

    private static int startVertex;

    private static int maxVertex;
    private static int graphNum;

    private static int[] incomingEdges;

    private void initGraph(int[][] edges) {
        maxVertex = 0;

        for (int[] edge : edges) {
            maxVertex = Math.max(maxVertex, Math.max(edge[0], edge[1]));
        }

        visited = new boolean[maxVertex + 1];
        incomingEdges = new int[maxVertex + 1];
        graph = new ArrayList<>(maxVertex + 1);

        for (int i = 0; i <= maxVertex; i++) {
            graph.add(new LinkedList<>());
        }

        for (int i = 0; i < edges.length; i++) {
            graph.get(edges[i][0]).add(edges[i][1]);//단방향 그래프
            incomingEdges[edges[i][1]]++;
        }
    }
    public int[] solution(int[][] edges) {
        int[] answer = new int[4];
        //그래프 초기화
        initGraph(edges);

        //시작 정점 찾기 + 전체 그래프 갯수 찾기
        startVertex = findCreatedVertex();
        graphNum = graph.get(startVertex).size();
        answer[0] = startVertex;
        //시작 정점 연결 끊기.
        removeEdgesFromCreatedVertex(startVertex);

        //막대 그래프 갯수 찾기.
        //들어오는 간선이 없거나, 나가는 간선이 없는 vertex의 갯수이다.
        answer[2] = countBarGraphs();

        //8자모양 그래프 갯수 찾기.
        //둘어오는 간선 2개, 나가는 간선2개인 vertex의 갯수이다.
        answer[3] = countEightShape();
        answer[1] = graphNum - (answer[2] + answer[3]);

        System.out.println(countIncomingEdges(maxVertex-1));
        return answer;
    }



    private int countBarGraphs() {
        int count = 0;
        for (int i = 1; i < graph.size(); i++) {
            if (i == startVertex) {
                continue;
            }
            if (graph.get(i).isEmpty()) {//나가는게 없다.
                count++;
                visited[i] = true;
            }
        }
        return count;
    }

    private int countEightShape() {
        int count = 0;
        for (int i = 1; i < graph.size(); i++) {
            if (!visited[i]) {
                if (graph.get(i).size() == 2 && countIncomingEdges(i) == 2) {
                    System.out.println(i);
                    count++;
                }
            }
        }
        return count;
    }

    private int findCreatedVertex() {
        //들어오는 거의 갯수가 없고, 나가는 것만 2개 이상인 점.
        int createdVertex = -1;
        for (int i = 1; i < graph.size(); i++) {
            if (graph.get(i).size() >= 2 && countIncomingEdges(i) == 0) {
                createdVertex = i;
                break;
            }
        }
        visited[createdVertex] = true;
        return createdVertex;
    }

    private int countIncomingEdges(int vertex) {
        return incomingEdges[vertex];
    }

    private void removeEdgesFromCreatedVertex(int vertex) {
        for(int end:graph.get(vertex)){
            incomingEdges[end]--;
        }
        graph.set(vertex, new LinkedList<>());
    }
}