[프로그래머스] 거스름돈(Java)

프로그래머스 거스름돈

전형적인 Level 3의 동적계획법 문제입니다. DP 문제를 푸는 요령을 이 기회에 제대로 익히게 해준 문제입니다.

DP의 핵심은 과거에 저장해둔 값을 바탕으로 현재 값을 도출해내는 것입니다.
그러므로 어떠한 의미있는 과거의 값을 저장해두고, 어떻게 현재 값을 도출하는데 과거의 값을 이용할지를 생각해보고 점화식을 세워야 합니다.

이를 알기 위해서는 다음과 같은 방식으로 풀이를 진행해야 합니다.

1. 일정량의 데이터를 직접 손으로 작성해보기
2. 이전값들을 이용해서 현재 값을 구할 수 있는 방식을 찾아내기
3. 찾아낸 방식을 점화식으로써 코드에 적용하기

DP의 문제의 대부분은 막상 점화식으로 코드를 작성해보면 보통 짧고 단순하기 때문에, 2번이 핵심이라고 볼 수 있습니다.

풀이법

1. 일정량의 데이터를 직접 손으로 작성해보기
   

2. 이전 값들을 이용해서 현재 값을 구할 수 있는 방식을 찾아내기
   
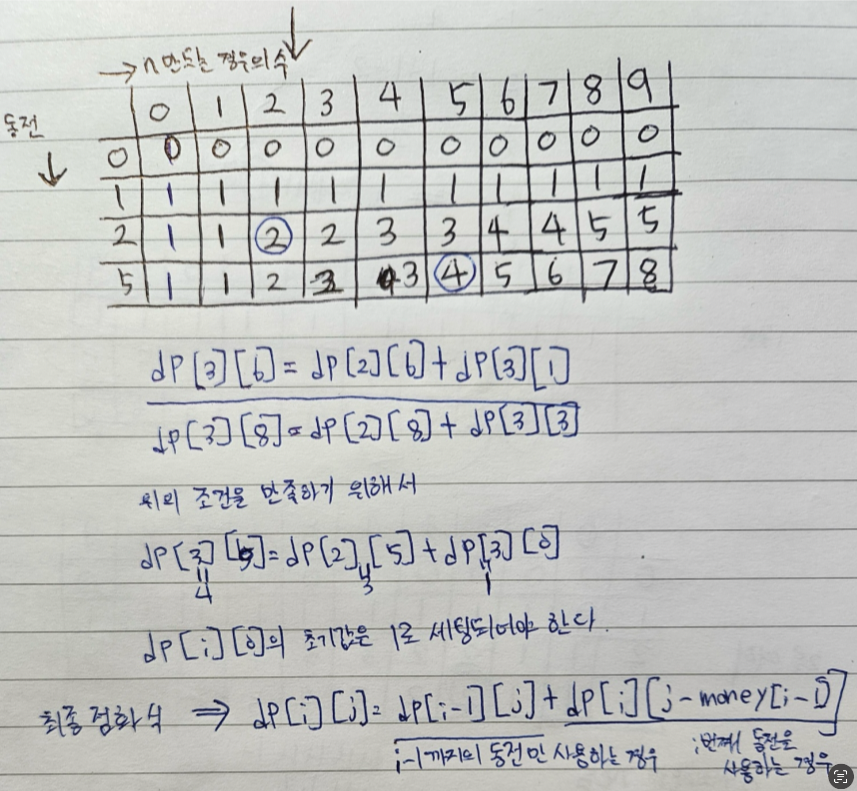
   도출해낸 점화식: dp[i][j]=dp[i-1][j]+dp[i]j-money[i-1]]
   현재 값 만들기 위한 경우의 수 = 과거의 동전들로만 만들 수 있는 경우 + 현재 동전을 사용하여 현재 값을 만들 수 있는 경우의 수
   로 분리해서 생각해야 함을 알 수 있었다.

3. 찾아낸 방식을 점화식으로써 코드에 적용하기

class Solution {

    private int[][] dp;

    public int solution(int n, int[] money) {

        dp = new int[money.length + 1][n + 1];//이차원 배열 생성

        for (int i = 1; i <= money.length; i++) {
            for (int j = 0; j <= n; j++) {
                if (j == 0) {
                    dp[i][j] = 1;//맨 첫 열은 1로 초기화
                } else if (j - money[i-1] >= 0) {
                    dp[i][j] = (dp[i - 1][j] + dp[i][j - money[i - 1]]) % 1000000007;
                } else
                    dp[i][j] = dp[i - 1][j];
            }
        }

        return dp[money.length][n];
    }
}

깨달은 점

1. dp문제에 2차원 배열이 거의 항상 이용된다.
2. 일정량의 데이터를 직접 손으로 작성하자.
3. 어떻게 과거의 값이 현재의 값을 구하는데 사용이 되는지 철저하게 파악해 점화식을 세운다.

Dynamic programming은 대체적으로 코드가 매우 간결하다. 점화식을 생각해내는 것이 난이도가 있는데 위와 같은 단계를 거쳐 논리적으로 생각해보면 풀 수 있을 것 같다는 생각이 들었다.
관련된 문제들을 좀 더 풀어보면서 체득해야겠다.