Convolutional Neural Network Compression for Embedded Systems

최근 합성곱 인공 신경망은 Image classification, Object detection, Image segmentation, Monocular depth estimation 등 다양한 곳에 활용되고 있다. 합성곱 인공 신경망은 기존 컴퓨터 비젼 알고리듬 보다 우수한 성능을 보이지만 많은 연산량을 요구하기에 드론과 같은 모바일 로봇에 탑재되는 임베디드 시스템에 적용되기에는 실시간성 확보 측면에 있어 많은 제약이 존재한다. 이러한 문제를 해결하기 위해 Pruning, Quantization, Knowledge distillation, Tensor decomposition 등과 같은 인공 신경망 경량화 알고리듬이 제안되었으며 본 포스트에서는 Tensor decomposition을 정리하고 합성곱 인공 신경망에 대해 어떤식으로 적용할 수 있는지에 대해 소개하고자 한다.

Tensor

Tensor는 Vector $\mathbb{V}\in \mathbb{R}^{I}$, Matrix $\mathbb{M}\in \mathbb{R}^{I\times J}$와 같이 Scalar 값을 담을 수 있는 다차원 배열로 다음과 같이 표현될 수 있다.

$\mathbb{T} \in \mathbb{R}^{I_{1}\times I_{2}\times ...\times I_{n}}$.

Convolutional Neural Network (CNN)

합성곱 인공 신경망의 가중치 $\mathbb{K}$는 Kernel size $K_{1}\times K_{2}$와 Input channel $C_{in}$과 Output channel $C_{out}$ 으로 구성된다.
즉, 합성곱 인공 신경망의 가중치 $\mathbb{K}$는 4차원 Tensor로 표현된다.

$\mathcal{K}\in \mathbb{R}^{K_{1}\times K_{2}\times C_{in} \times C_{out}}$.

Tensor Decomposition

Singular Value Decomposition (SVD)을 이용하면 하나의 Matrix를 여러 개의 Matrix들로 분해할 수 있는 것과 같이 Tensor 또한 여러 개의 Tensor들의 조합으로 표현될 수 있으며 이러한 알고리듬을 Tensor decomposition이라 한다. 즉, Tensor decomposition의 목적은 다음과 같다.

$argmin_{\hat{\mathcal{K}}}||\mathcal{K}-\hat{\mathcal{K}}||$

Tensor decomposition은 CP decomposition, Tucker decompositoin, Tensor-train decomposition, Tensor-ring decomposition과 같이 여러 개의 알고리듬들이 존재하지만 본 포스터에서는 앞의 2개의 알고리듬을 간략히 소개하고자 한다.

CANDECOMP/PARAFAC Decomposition (CP Decomposition)

• CP decomposition은 주어진 Tensor $\mathcal{K}$를 Rank-1 tensor들의 합으로 표현한다.
  즉, $\hat{\mathcal{K}}\approx \sum\limits_{t=1}^{T}{\lambda_{t}\cdot a_{t}\circ b_{t}\circ c_{t} \circ d_{t}}$ 으로 표현될 수 있다.
  여기서 $\circ$는 Outer product를 의미하고 $\lambda$는 Normalized 된 Vector $a,b,c,d$ 의 상관 계수다.
• 따라서, $argmin_{\hat\mathcal{K}}||\mathcal{K}-\sum\limits_{t=1}^{T}{\lambda_{t}\cdot a_{t}\circ b_{t}\circ c_{t} \circ d_{t}}||$ 을 푸는 최적화 문제로 바뀌게 되고 이를 Alternating Least Square (ALS) 알고리듬을 적용하여 Decomposition 할 수 있다.
• ALS 알고리듬은 Decomposition 결과와 근사화하고자 하는 Tensor의 차이가 특정 Threshold 미만이 될 때 까지 반복적으로 최적화 하는 기법이라 생각하면 된다.
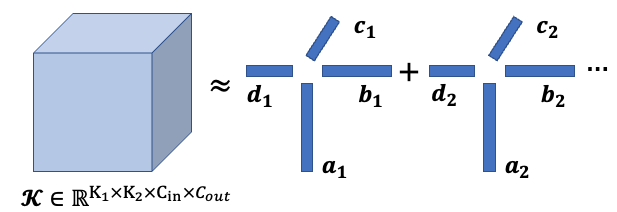
• CP decomposition을 그림으로 표현하면 다음과 같다.

CP decomposition: $\lambda$가 1인 경우

• CP decomposition은 Rank-1 tensor들의 합으로 기존 Tensor를 근사화하므로 근사화 성능이 뒤에 후술할 Tucker decomposition보다 뒤떨어진다.

Tucker Decomposition: Generalization of CP Decomposition

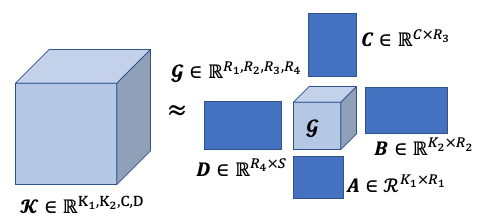
• Tucker decomposition은 기존의 텐서 $\mathcal{K}$를 Core Tensor와 Factor matrices로 분해한다. 여기서 Core Tensor는 Factor matrices들관의 상관관계를 표현하는 스칼라 값들로 채워진다.

Tucker decomposition: Core tensor $\mathcal{G}$와 Factor matrices

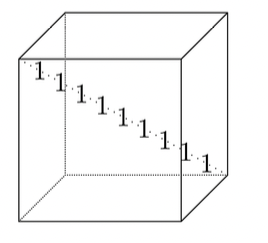
• CP decomposition의 경우 Core tensor가 Super diagonal 형태로 대각 성분은 $\lambda$로 채워지게 되지만 Tucker decomposition은 Super diagonal 형태가 아닌 대각 성분 외의 값도 가지게 된다. 따라서 Tucker decomposition은 CP decomposition의 일반화라 볼 수 있다.

Super diagonal (fig. from $^{[1]}$)

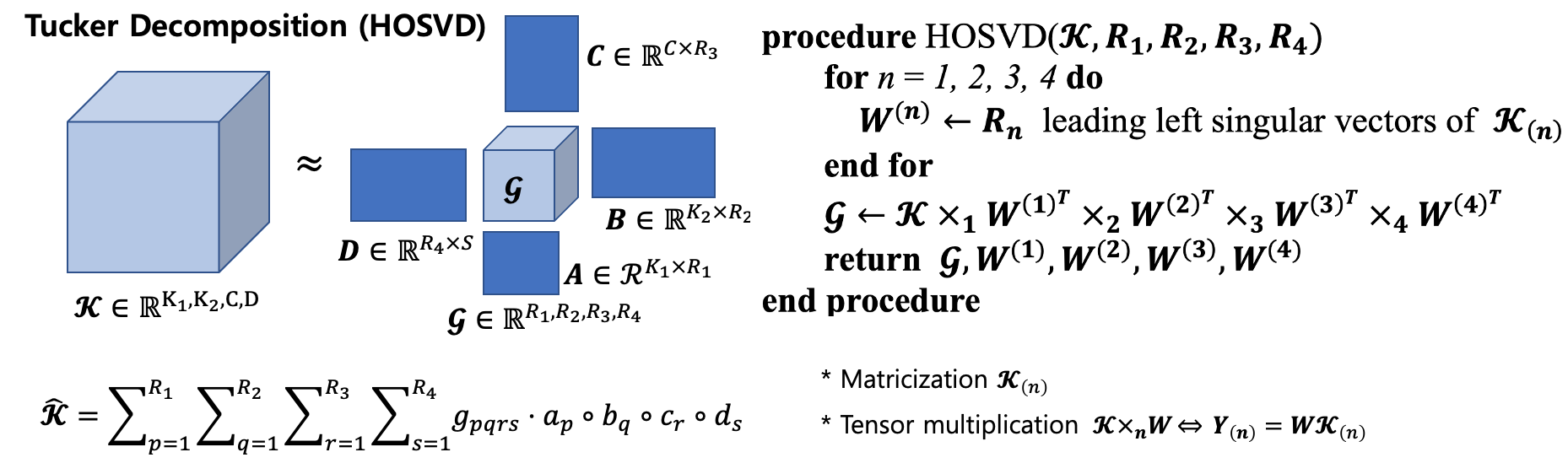
• Tucker decomposition은 Higher Order Singular Value Decomposition (HOSVD)라고도 불리는데 그 이유는 Tucker decomposition을 수행할 때, SVD가 사용되기 때문이다. HOSVD의 psuedo-code는 다음과 같다.

Tucker decomposition (HOSVD) pesudo-code

• HOSVD는 주어진 Tensor $\mathcal{K}$를 각 axis (또는 mode)에 대해 행렬화 (Matricization)한 후 SVD를 진행하고, 주어진 Rank $\mathcal{R_1}, \mathcal{R_2}, \mathcal{R_3}, \mathcal{R_4}$만큼의 left singular vectors을 취해 factor matrices들로 저장한다. 각 axis에 대해 모두 factor matrix를 구한 후 이를 이용하여 Core tensor $\mathcal{G}$를 계산할 수 있다.

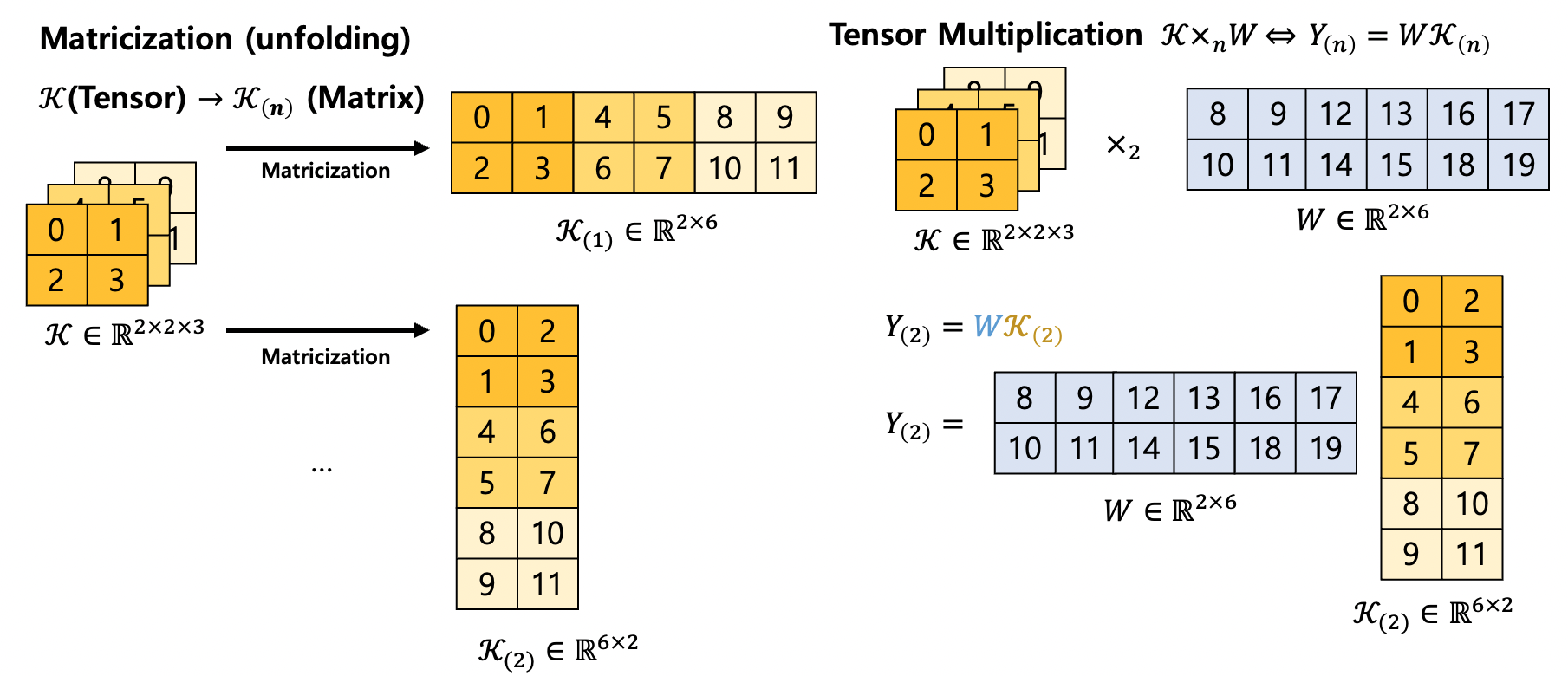
• Matricization과 Tensor multiplication의 예시는 다음과 같다.

Matricization and Tensor multiplication

• Higher Order Orthogonal Iteration (HOOI)
  HOOI 알고리듬은 Tucker decomposition + ALS 이다.

How to choose the rank adaptively?

Tucker decomposition은 입력으로 factor matrices들을 계산하기 위한 rank를 넣어줘야하며 이 rank 값들에 따라 근사화 성능이 달라진다. 따라서 기존의 Tensor를 잘 근사화 하면서도 최대한 적은 파라미터를 가질 수 있도록 rank를 설정해줘야 하는데 이를 계산해주는 알고리듬은 크게 3가지가 있다.

• Variational Bayesian Matrix Factorization (VBMF)
  VBMF는 Variational inference를 이용한 행렬 분해 알고리듬으로 Nakajima, S. et al$^{[2][3]}$가 VBMF의 해의 결과가 truncated SVD라는 연구를 진행하였다.
  Tucker decomposition이 행렬화 하는 점을 활용하여 Tucker decomposition을 하기 전 각 axis에 대해
  matricization을 진행하고 VBMF를 적용하면 left singular vectors를 구하기 위한 rank를 adaptive하게 추정할 수 있다.
  

VBMF의 HOSVD 적용

• Genetic algorithm
• Reinforcement learning
  Genetic algorithm과 Reinforcement learning을 활용하여 rank를 추정하는 연구도 진행되고 있으나 VBMF보다 나은 연구를 찾아 볼 순 없었다
  (괜찮은 논문 아시는 분 계시면 제보좀...)

Tensor Decomposition for Neural Network Compression

CP Decomposition은 기존의 합성곱 인공 신경망의 가중치를 4개의 Tensor로 분해한다.

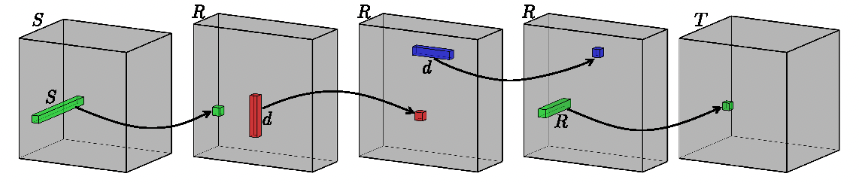
• 4개의 Tensor를 신경망 레이어로 표현하면 2개의 Partial Depth-wise Convolution과 2개의 Point-wise Convolution으로 표현된다.

CP decomposition 적용 결과: Point-wise convolution (초록색) 적용 후 각 축에 대한 Depth-wise convolution (빨간, 파란색) 적용 후 마지막에 다시 Point-wise convolution이 적용된다. fig. from [4]

Tucker-2 Decompsition은 기존의 합성곱 인공 신경망의 가중치를 3개의 Tensor로 분해한다.

• Convolution kernel을 decomposition하면 Local representation power가 감소하게 되므로 일반적으로 커널의 사이즈는 보존한다.
  (Convolutional kernel 사이즈의 경우 $3\times3$과 같이 이미 충분히 작은 경우가 대다수이다.)
• 따라서 Point-wise convolutional layer를 활용하여 $C_{in}$과 $C_{out}$의 차원을 줄이는 식으로 경량화가 가능하다. 즉, Tucker-2 decomposition을 적용한다.
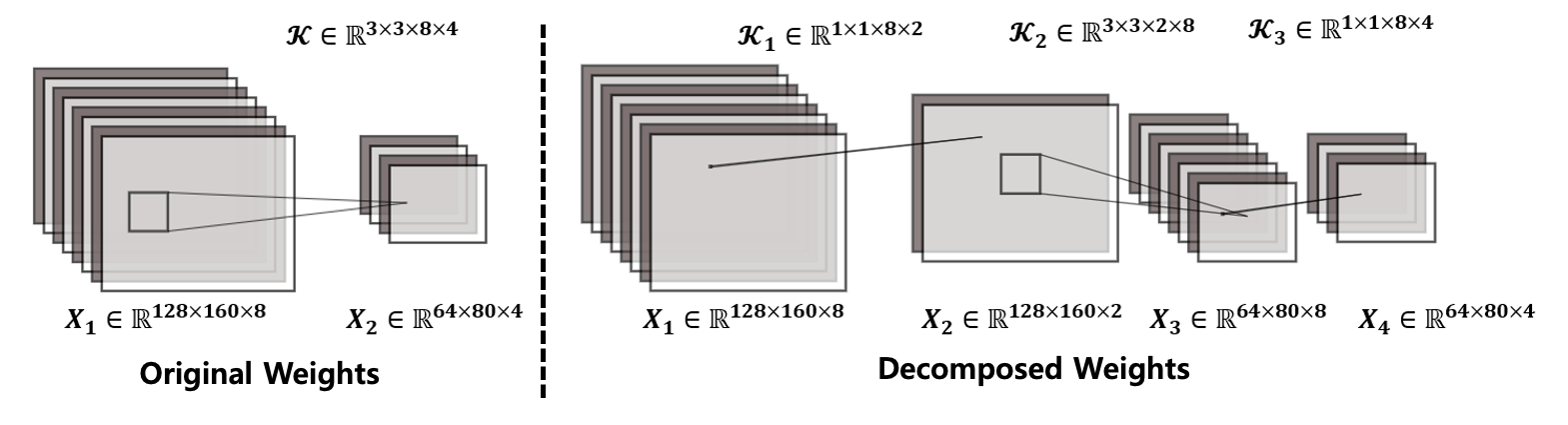
• Tucker-2 decomposition은 기존 Standard convolution layer를 1개의 작은 Standard Convolution (Core tensor)과 2개의 Point-wise Convolution (Factor matrices)으로 분해한다.

Tucker decomposition으로 CNN 분해 예시: 같은 입력에 대해 출력은 같으나 CNN 파라미터의 수가 $3\times3\times8\times4=288$에서 ($1\times1\times8\times2$) +($3\times3\times2\times8$)+($1\times1\times8\times4$)=192개로 줄어듦

Source Code

공개예정..

Reference

[1] Kolda, Tamara G., and Brett W. Bader. “Tensor decompositions and applications.” SIAM
review, Vol. 51, No. 3, pp. 455-500, 2009.
[2] Nakajima, S., Sugiyama, M., Babacan, S. D., and Tomioka, R, “Global analytic solution
of fully-observed variational Bayesian matrix factorization,” The Journal of Machine
Learning Research, Vol. 14, No. 1, pp. 1-37, 2013.
[3] Nakajima, S., Tomioka, R., Sugiyama, M., and Babacan, S. “Perfect dimensionality
recovery by variational Bayesian PCA,” Advances in neural information processing
systems (NIPS), Vol. 25. 2012.
[4] Lebedev, V., Ganin, Y., Rakhuba, M., Oseledets, I., & Lempitsky, V., "Speeding-up convolutional neural networks using fine-tuned cp-decomposition," arXiv preprint arXiv:1412.6553, 2014.