1-6 [구간 합 실전 문제] 연속된 자연수의 합 구하기 (백준 2018)

그린·2023년 3월 5일

Do It! 알고리즘 코딩테스트 with JAVA

목록 보기

8/11

투 포인터

투 포인터 : 2개의 포인터로 알고리즘의 시간 복잡도를 최적화함

문제 : https://www.acmicpc.net/problem/2018

1) 문제 분석하기

N의 범위가 엄청 큼. → 이런 상황에서는 O(nlogn)의 시간 복잡도 알고리즘을 사용하면 제한 시간을 초과함

⇒ O(n)의 시간 복잡도 알고리즘을 사용해야 함.

⇒ 이럴 때 자주 사용하는 방법이 투 포인터.

⇒ 시작 인덱스와 종료 인덱스를 지정하여 연속된 수를 표현할 것이다.

2) 손으로 풀어 보기

배열의 값을 인덱스 자체로 하면 된다.

두개의 포인터를 맨 앞자리로 옮길 것임.

sum = 1 → start_index와 end_index가 갖는 연속된 합의 크기

count = 1 → 15 하나만으로도 15를 만들 수 있으므로 미리 넣고 초기화함
다음의 투 포인터 이동 원칙을 활용해 배열의 끝까지 탐색하면서 합이 N이 될 경우의 수를 구함

start_index를 오른쪽으로 한 칸 이동하는 것 = 연속된 자연수에서 왼쪽 값을 삭제하는 것
- sum > N :
  - sum = sum - start_index;
  - start_index++;
- sum < N :
  - end_index++;
  - sum = sum + end_index;
- sum == N :
  - end_index++;
  - sum = sum + end_index;
  - count++; → 연속된 수로 표현하는 것을 찾았다
end_index가 N이 될 때까지 반복

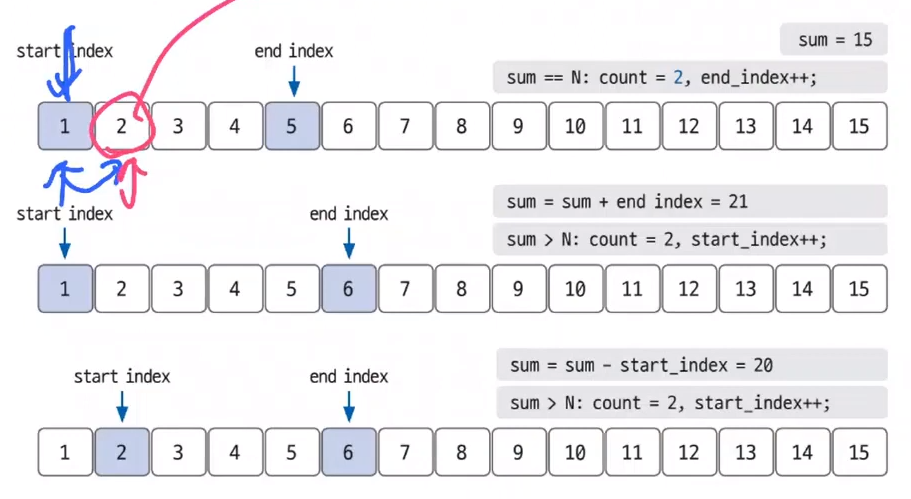
start_index = 1, end_index = 1일 때 sum = 1 < 15 → end_index++;

start_index = 1, end_index = 2일 때 sum = 3 < 15 → end_index++;

start_index = 1, end_index = 3일 때 sum = 6 < 15 → end_index++;

start_index = 1, end_index = 4일 때 sum = 10 < 15 → end_index++;

start_index = 1, end_index = 5일 때 sum = 15 == 15 → count ++; end_index++; (count = 2)

start_index = 1, end_index = 6일 때 sum = 21 > 15 → start_index++;

start_index = 2, end_index = 6일 때 sum = 20 > 15 → start_index++;

start_index = 3, end_index = 6일 때 sum = 18 > 15 → start_index++;

start_index = 4, end_index = 6일 때 sum = 15 == 15 → count++; end_index++; (count = 3)

…

이게 왜 시간 복잡도가 N일까?

start_index와 end_index를 N까지 한번 싹 도니까 총 2N의 시간복잡도가 걸린다.

따라서 O(N)

3) 슈도코드 작성하기

N 변수 저장
사용 변수 초기화(count = 1, start_index = 1, end_index = 1, sum = 1)
// count = 1 : 자기 자신 하나로 이루어진 경우의 수를 미리 저장함 (뒤쪽을 어떻게 하는지에 따라 달라짐)

while (end_index != N) { // s, e 이동 원칙에 따라 반복
	if (sum == N) count++, end_index++, sum값 변경
	else if (sum > N) sum값 변경, start_index 증가
	else if (sum < N) end_index 증가, sum값 변경
}
count 출력하기

4) 실제 코드 작성하기

문제를 어떻게 접근해야 할지 감이 안 와서.. 해설의 원리까지 보고 구현한 코드

/*
 * @author Minyeong Park
 * @date 2023.03.05.
 * 수들의 합 5
 * 원리 참고 : https://www.inflearn.com/course/lecture?courseSlug=%EB%91%90%EC%9E%87-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%BD%94%EB%94%A9%ED%85%8C%EC%8A%A4%ED%8A%B8-%EC%9E%90%EB%B0%94&unitId=148341
 * 문제 링크 : https://www.acmicpc.net/problem/2018
 */

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int[] arr = new int[n+1];
        for (int i = 1; i <= n; i++) { // 아예 배열도 안 만들어도 됨!
            arr[i] = arr[i-1] + i;
        }

        int start_idx = 1;
        int end_idx = 1;
        int count = 0;

        while (start_idx <= n && end_idx <= n) {
            int sum = arr[end_idx] - arr[start_idx-1];
            if (sum < n) {
                end_idx++;
            } else if (sum > n) {
                start_idx++;
            } else {
                count++;
                end_idx++;
            }
        }

        System.out.println(count);
    }
}

강의에서 푸신 코드 (위 코드에서 중요 내용만 수정함)

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        int start_idx = 1;
        int end_idx = 1;
        int count = 1;
        int sum = 1;

        while (end_idx != n) {
            if (sum < n) {
                end_idx++;
                sum = sum + end_idx;
            } else if (sum > n) {
                sum = sum - start_idx; // 기존에 있었던 것을 빼주고
                start_idx++;           // 인덱스를 증가
            } else { // 같은 경우
                count++;
                end_idx++;
                sum = sum + end_idx;
            }
        }

        System.out.println(count);
    }
}