https://www.acmicpc.net/problem/1940

1) 문제 분석하기

시간 복잡도 고려해보기 → 두 재료의 번호의 합, 즉 크기를 비교하므로 값을 정렬하면 문제를 좀 더 쉽게 풀 수 있음.

N의 최대 범위가 15000이므로 O(nlogn) 시간복잡도 알고리즘을 사용해도 문제 없음.

일반적으로 정렬 알고리즘의 시간 복잡도 : O(nlogn)

입력받은 N개의 재룟값을 정렬한 다음 양쪽 끝의 위치를 투 포인터로 지정해 문제에 접근해 보겠음 → 많이 풀다보면…

각 재료들이 한 번 쓰고 없어지네? 2개를 뽑아서 값을 만들면 답이 나오는구나.. → 어떻게 하면 빨리 찾을 수 있을까? → 투포인터!

이렇게 생각 가능함

2) 손으로 풀어 보기

1. 재료 데이터 배열을 오름차순 정렬
2. 정렬을 해놨기 때문에 만약 min + max < m 인 경우 min을 하나 다음으로 옮기면 된다!
   

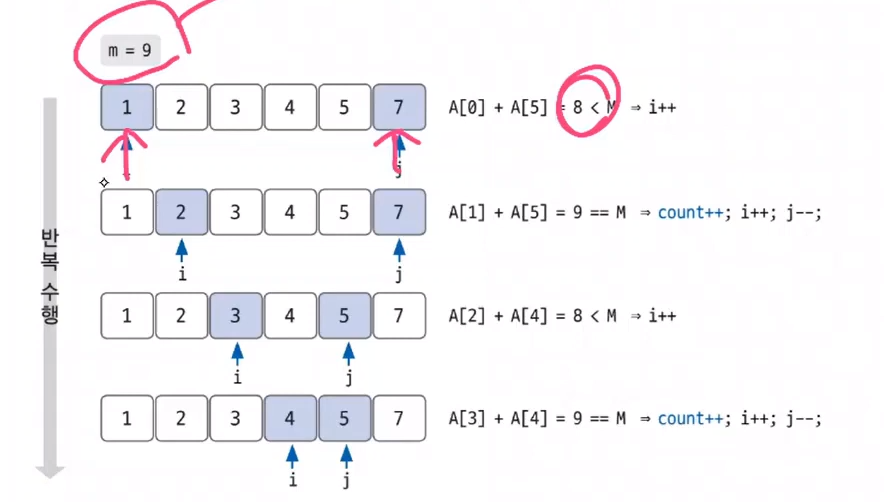
만약 min + max == m과 같은 경우를 찾으면 이후에 min은 오른쪽으로, max는 왼쪽으로 한칸씩 이동

시간 복잡도 : N번 만에 탐색 가능!!

정렬하는 시간 복잡도 O(nlogn)이 더 크기 때문에 전체 시간 복잡도는 O(nlogn)

3) 슈도코드 작성하기

N(재료의 개수), M(갑옷이 되는 번호) 저장
for (N만큼 반복)
{
	재료 배열 저장
}

재료 배열 정렬

while (i < j) {
	if (재료 합 < M) 작은 번호 재료++;
	else if (재료 합 > M) 큰 번호 재료--;
	else 경우의 수 증가, 양쪽 index값 각각 변경
}
count 출력

4) 실제 코드 작성하기

import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int m = Integer.parseInt(br.readLine());
        StringTokenizer st = new StringTokenizer(br.readLine());
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        Arrays.sort(arr);
        int start_idx = 0;
        int end_idx = arr.length - 1;
        int count = 0;
        while (start_idx < end_idx) {
            int sum = arr[start_idx] + arr[end_idx];
            if (sum < m) {
                start_idx++;
            } else if (sum > m) {
                end_idx--;
            } else if (sum == m) {
                start_idx++;
								end_idx--;
                count++;
            }
        }
        System.out.println(count);
    }
}