이번 글은 DFS만 정리했고, BFS는 다음 글에서 정리했다.
DFS와 BFS 모두 탐색했던 노드에 대해 방문 처리를 남겨줘야 한다!
visited 등의 리스트 자료형으로 표현하고, True 와 False를 활용해 방문 여부를 남겨주면 편하다.
DFS란?
Depth-First Search의 약자로 깊이-우선 탐색이라고도 불린다. 그래프에서 깊은 부분을 우선적으로 탐색하는 구조이다. 스택 구조를 활용한다.
DFS를 알기 전에 그래프의 기본 구조부터 알아야 한다.
그래프의 기본 구조
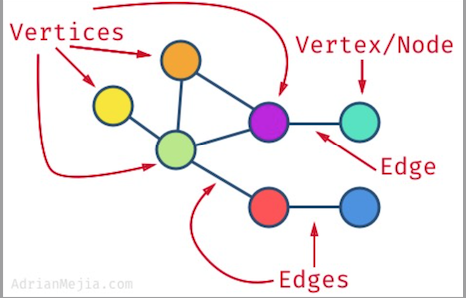
노드(Node)=정점(Vertex)와 같은 말이라고 생각하면 된다.
또, 두 노드(Node)가 간선(Edge)로 연결되어 있다면 '두 노드는 인접(Adjacent)하다'고 말한다.
간선(Edge)은 비용이나 거리로 생각하면 된다.
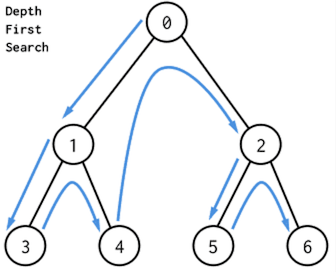
그래프에 대한 기본 구조를 알았으면, 아래 구조에서 0부터 화살표와 같은 순서로 탐색을 하게 된다.(작은 번호의 노드 부터 탐색 조건)
이 때, 움직임은 스택 구조를 생각하면 되는데 그림으로 순서를 쉽게 표현한 곳(https://hongku.tistory.com/157)을 봐보자.
그래프 표현 방법 2가지
1. 인접 행렬(Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현
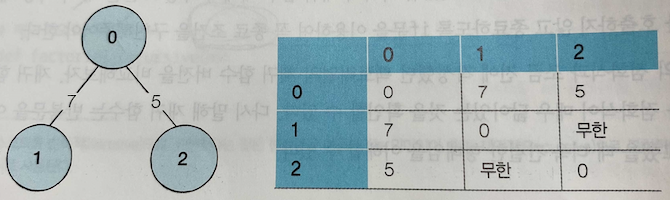- 연결이 되어있지 않은 노드끼리의 간선(Edge)은 무한(Infinity)이라고 생각하고 작성한다.
- 실제 코드에서 무한(Infinity)은 논리적으로 답이 될 수 없는 999999999 등의 값으로 한다.
이를 코드화 해보면 아래와 같다.
Inf = 999999999 #무한의 간선 선언
graph = [ #인접 행렬 표현(2차원 리스트를 활용)
[0,7,5],
[7,0,Inf],
[5,Inf,0],
]
<출력값>
print(graph)
>>> [[0,7,5], [7,0,999999999], [5,999999999,0]]
2. 인접 리스트(Adjacency List) : 리스트로 그래프의 연결 관계를 표현
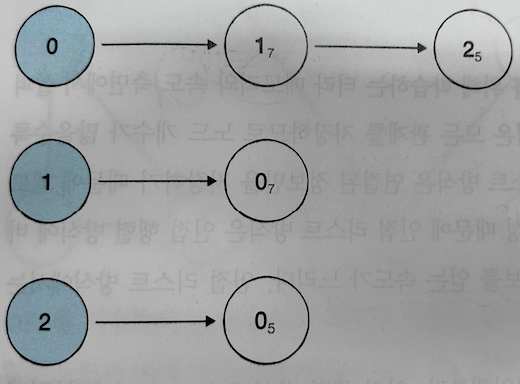- 단순히 노드에 인접한 노드와 간선의 정보만 각각 List로 나타내는 것이다.
이를 코드화 해보면 아래와 같다.
graph = [[] for _ in range(3)] #행(Row)이 3개인 2차원 리스트
graph[0].append((1,7)) # 노드 0에 연결된 노드 정보 저장(노드, 간선)
graph[0].append((2,5)) # 튜플로 노드, 간선 append
graph[1].append((0,7)) # 노드 1에 연결된 노드 정보 저장(노드, 간선)
graph[2].append((0,5)) # 노드 2에 연결된 노드 정보 저장(노드, 간선)
<출력값>
print(graph)
>>> [[(1,7),(2,5)], [(0,7)], [(0,5)]]
DFS 구현하기
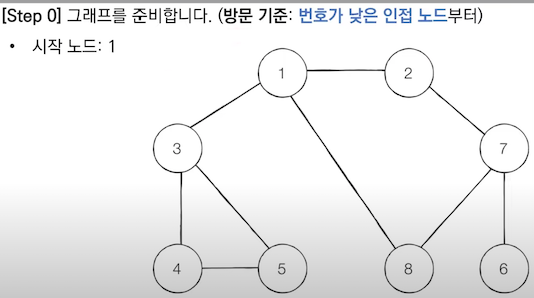
아래와 같은 그래프를 DFS로 구현해보자.
def dfs(graph, node, visited):
visited[node] = True #현재 노드를 방문 처리
print(node, end=" ") #현재 노드 출력
#현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[node]: #주어진 노드에 연결된 노드를 순차적으로 방문
if not visited[i]: #i번 노드를 방문한 적이 없다면
dfs(graph, i, visited)
visited=[False]*9 #방문 여부 처리하는 visited라는 List 만들기
#이 때, 보통 문제에서 0번 노드가 없어서, 0은 항상 False가 유지
graph = [ #graph 만들기
[], #0번 노드는 보통 문제에서 없으므로, 헷갈리게 하지 않기 위해 빈 리스트로 생성만 해 둠
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
dfs(graph,1,visited)
<출력값>
>>> 1 2 7 6 8 3 4 5 리스트 역순 꿀팁!
문제를 풀다가 시간복잡도? 속도 관점에서 궁금해서 Test해봤다.
먼저, List를 역순으로 바꿀 수 있는 경우는 크게 3가지(?)인 것 같다.
1. reversed(List) 활용
2. List.sort(reverse=True) 활용
3. New_List=List[::-1]
1억 개의 원소를 가진 List로 비교해본 결과, 1번의 reversed()함수 활용이 압도적으로 빠른 것을 확인할 수 있었다. 그 다음 2번의 sort()함수 활용, 3번의 [::-1] 활용 순으로 시간이 적게 걸렸다.
3번이 약 2.3초, 2번이 약 1.3초이며 1번은 무려 0.000005초 밖에 안걸렸다...
그 차이는 놀랍게도 거의 만배 차이였다.
reversed(List)를 활용하자 !
흑.. 1번의 reversed()만 쓰면, list화 되는 것이 아니었다.. 결국 시간은 도긴개긴이다 하핫
+정말 멍청이었다..ㅋㅋㅋㅋ 심지어 reversed는 크기 역순으로 배열을 해주는 게 아니라, 단순 index를 역순으로 배열해주는 것이었다...
ex) reversed([1,4,3,2]) → [2,3,4,1]
만배 차이!!!!!!!!WOW