201223 개발일지(16일차) - 파이썬에서 bisect() 함수 활용 feat.백준 8983번

bisect란?

bisect의 사전적 의미는 이등분(2등분)이다. 파이썬에서 bisect 모듈을 활용하면 이분 탐색(이진 분할 알고리즘 활용)을 통해 정렬된 List에 'a'라는 값이 어디에 들어가면 되는지 index로 알려준다.

bisect.bisect() 와 bisect.bisect_left()

bisect 모듈에는 크게 bisect()와 insort() 함수밖에 없다.
그 중 bisect(), bisect_left(), bisect_right()을 보자.

• bisect.bisect() : a=[1,3,5,7]이라는 정렬된 List가 있을 때, 정수 2는 어디에 넣을 수 있을까? 1과 3 사이에 넣을 수 있겠지. 그럼 이 때 bisect()함수는 그 위치의 index값인 1을 return해준다.
  즉, bisect(a)의 return 값은 0~4이다. 만약 정수 0을 a에 넣고자 한다면 0을 return할 것이고, 정수 8을 a에 넣고자 한다면 4를 return해 줄 것이다.

질문 ? : 그럼 5를 넣고자 한다면 뭐라고 return해줄까? 즉, 정렬된 List에 넣고자 하는 값이 이미 List에 있을 때 고민이 생기는데 이 고민의 답을 2개로 나누어 준 것이 bisect_left()이다.
무슨말이냐면 b=[1,3,5,5,5,7]에 정수 5의 bisect()값은 5이다. 같은 값이 이미 List에 있다면 같은 값들의 가장 오른쪽 index를 return해준다.

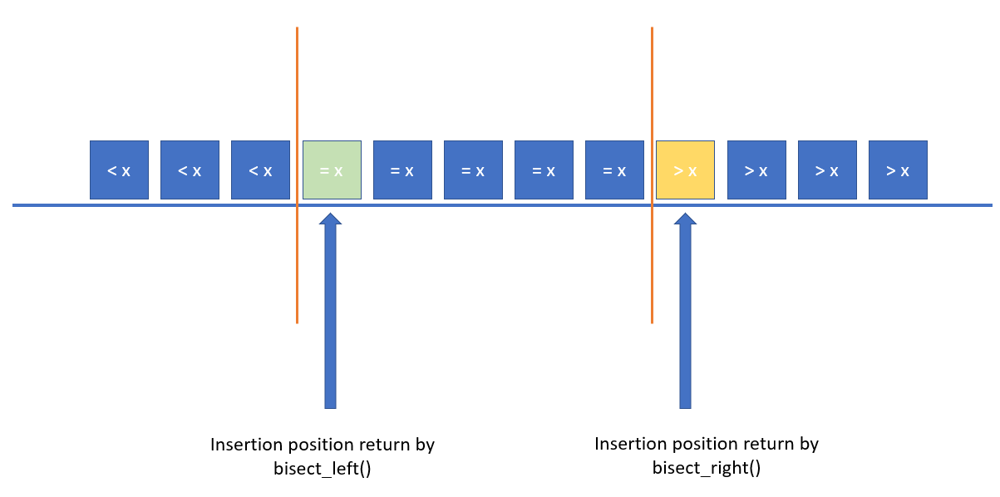
• bisect.bisect_left() : bisect()함수와 동일하나 위의 질문에 대한 나머지 대답을 해결해준다. 즉, b=[1,3,5,5,5,7]에 정수 5의 bisect_left()값은 2이다. bisect()와 반대로 같은 값이 이미 List에 있다면 같은 값들의 가장 왼쪽 index를 return해준다.
• bisect.bisect_right() : bisect()와 동일한 함수이다. 위의 질문과 같은 이유로 헷갈릴 수 있어서 bisect_right()라는 이름의 함수를 추가적으로 사용할 수 있게한 것 같다.
  

파이썬에서 bisect 모듈

이 모듈은 정렬된 리스트를 삽입 후에 다시 정렬할 필요 없도록 관리할 수 있도록 지원합니다. 값비싼 비교 연산이 포함된 항목의 긴 리스트의 경우, 이는 일반적인 방법에 비해 개선된 것입니다. 이 모듈은 기본적인 이진 분할 알고리즘을 사용하기 때문에 bisect라고 불립니다. 소스 코드는 알고리즘의 실제 예로서 가장 유용할 수 있습니다 (경계 조건은 이미 옳습니다!).

다음과 같은 함수가 제공됩니다:

bisect.bisect_left(a, x, lo=0, hi=len(a))
정렬된 순서를 유지하도록 a에 x를 삽입할 위치를 찾습니다. 매개 변수 lo 와 hi는 고려해야 할 리스트의 부분집합을 지정하는 데 사용될 수 있습니다; 기본적으로 전체 리스트가 사용됩니다. x가 a에 이미 있으면, 삽입 위치는 기존 항목 앞(왼쪽)이 됩니다. 반환 값은 a가 이미 정렬되었다고 가정할 때 list.insert()의 첫 번째 매개 변수로 사용하기에 적합합니다.

반환된 삽입 위치 i는 배열 a를 이분하여, 왼쪽은 all(val < x for val in a[lo:i]), 오른쪽은 all(val >= x for val in a[i:hi])이 되도록 만듭니다.

bisect.bisect_right(a, x, lo=0, hi=len(a))
bisect.bisect(a, x, lo=0, hi=len(a))
bisect_left()와 비슷하지만, a에 있는 x의 기존 항목 뒤(오른쪽)에 오는 삽입 위치를 반환합니다.

반환된 삽입 위치 i는 배열 a를 이분하여, 왼쪽은 all(val <= x for val in a[lo:i]), 오른쪽은 all(val > x for val in a[i:hi])이 되도록 만듭니다.

bisect.insort_left(a, x, lo=0, hi=len(a))
a에 x를 정렬된 순서로 삽입합니다. a가 이미 정렬되었다고 가정할 때 a.insert(bisect.bisect_left(a, x, lo, hi), x)와 동등합니다. O(log n) 검색이 느린 O(n) 삽입 단계에 가려짐에 유념하십시오.

bisect.insort_right(a, x, lo=0, hi=len(a))
bisect.insort(a, x, lo=0, hi=len(a))
insort_left()와 비슷하지만, a에 x를 x의 기존 항목 다음에 삽입합니다.

(출처 : 파이썬 공식문서, https://docs.python.org/ko/3/library/bisect.html)

bisect를 활용한 문제 : 백준 8983번(사냥꾼)

직접 이분 탐색(pl, pr, pc 활용)으로 코드를 짜서 풀어도 되나 bisect와 친해지기 위해 bisect모듈을 활용했다.
이 때, bisect("사대의 x좌표 List", 동물의 x좌표)를 활용해서 풀었는데, 사대 x좌표를 벗어나는(bisect return값이 0 혹은 n) 동물들에 대해 생각해주지 않아 애먹었다.

풀이 코드는 아래와 같으며, 맨 아래 for문은 개선이 가능하다.(동은 도움)

import sys
import bisect
sys.stdin = open("input.txt", "r")

M, N, L= map(int, sys.stdin.readline().rstrip().split())
sandboxes=list((map(int, sys.stdin.readline().rstrip().split())))
animals=[list(map(int, sys.stdin.readline().rstrip().split())) for _ in range(N)]
sandboxes.sort()
bisects=[]
count=0

for animal in animals:
    bisects.append(bisect.bisect(sandboxes, animal[0]))

for i in range(len(animals)):
    if animals[i][0] >= sandboxes[-1] :                 #마지막 사대와 동물의 위치를 고려해야 한다!
        if animals[i][0] - (L - animals[i][1]) <= sandboxes[bisects[i] - 1] :
            count+=1
    elif animals[i][0] < sandboxes[0] :                 #맨 처음 사대와 동물의 위치를 고려해야 한다.
        if animals[i][0] + (L - animals[i][1]) >= sandboxes[bisects[i]] :
            count+=1
    else :                                              #그 사이의 사대들은 그대로 bisect값으로 구한 걸 이용
        if animals[i][0] - ( L - animals[i][1]) <= sandboxes[bisects[i]-1] or animals[i][0] + ( L - animals[i][1]) >= sandboxes[bisects[i]]:
            count+=1

#바로 위의 for문 개선
for j in range(N):
    if ( bisects[j] < M and sandboxes[bisects[j]] - animals[j][0] + animals[j][1] <= L) or (0 < bisects[j] and animals[j][0] - sandboxes[bisects[j]-1] + animals[j][1] <= L):
            count += 1

print(count)