나동빈님의 <이 것이 취업을 위한 코딩테스트다 with파이썬> 자료를 많이 참고하여, 정리했습니다.
동적 프로그래밍(Dynamic Programming)이란?
수학과 컴퓨터 공학, 그리고 경제학에서 동적 계획법(dynamic programming)이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다.
(출처 : 위키백과)
일단 이름 때문에 헷갈리지 말자. 1953년 벨만이라는 사람이 붙인 이름인데, 실질적으로는 "기억하며 풀기" 라고 생각하는 것이 심리적으로 좋을 것이다.
동적 프로그래밍(기억하며 풀기)은 큰 문제를 풀기 위해 작은 문제를 만들어 큰 문제를 풀어가는 방법이다.
동적 프로그래밍 활용 필수 조건 2가지
- 최적 부분 구조 : 큰 문제를 작은 문제로 나눌 수 있다.
- 중복되는 부분 문제 : 동일한 작은 문제를 반복적으로 해결한다.
동적 프로그래밍 방식(?) 2가지
아래와 같이 2가지로 나눌 수 있는데, 아래 피보나치 수열 문제를 예로 자세히 나누어 알아보자. 결론부터 말하면, 상향식 방식을 사용하는 것이 좋다.
- 하향식(Top-Down) : 큰 문제를 해결하기 위해 작은 문제를 호출한다고 하여, 이런 이름이다. 재귀함수를 이용하는 것이라고 보면 된다. 또, 메모이제이션(Memozation)을 활용하지만, 이는 동적 프로그래밍에만 국한된 개념은 아니다. 메모이제이션 뜻은 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념을 말한다.
- 상향식(Bottom-Up) : 동적 프로그래밍의 전형적인 형태로, 작은 문제로부터 차근차근 답을 도출해 나간다. 결과저장용 리스트를 dp테이블 이라고 한다.
3가지 방식으로 피보나치의 수 문제 풀기(재귀함수, 하향식, 상향식)
동적 프로그래밍의 쉬운 예인 피보나치의 수 문제를 재귀함수, 하향식, 상향식 3가지로 풀어보며 동적 프로그래밍을 익혀보자.
<재귀함수>
아래처럼 중복된 계산을 여러번 반복한다.
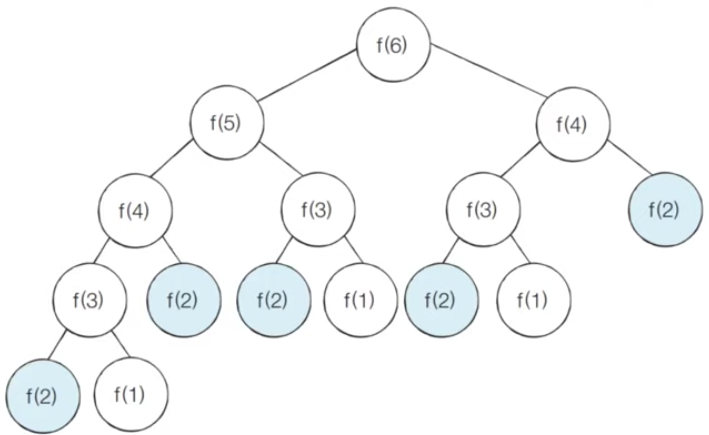
def fibo(x):
if x == 1 or x == 2 :
return 1
return fibo(x-1) + fibo(x-2)<하향식, 메모이제이션 활용>
기존에 기록된 값은 추가로 계산하지 않는다.
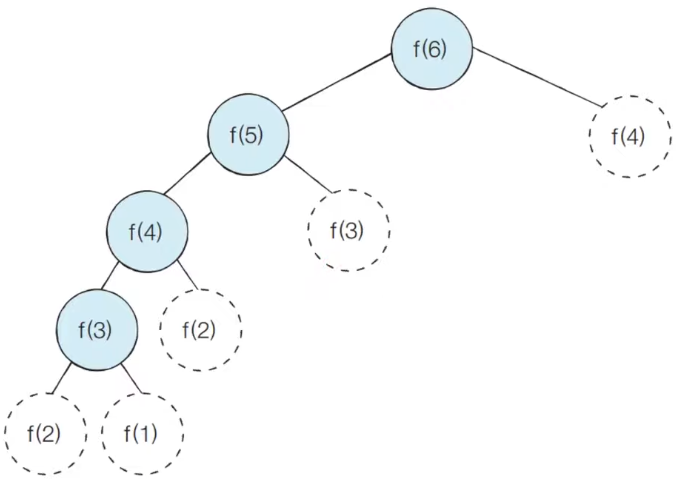
# 한 번 계산된 결과를 메모이제이션(Memozation)하기 위한 리스트 만들기
memoization = [0] * 100
def fibo(x):
if x == 1 or x == 2 :
return 1
# 이미 계산한 적 있다면 그 값을 그대로 반환
if memoization[x] !=0:
return memoization[x]
else :
#큰 곳에서 작은 곳으로 내려가는 하향식
memoization[x] = fibo(x-1) + fibo(x-2)
return memoization[x]<상향식, dp테이블 활용>
# 한 번 계산된 결과를 저장하기 위한 dp테이블 만들기
dp=[0]* 100
def fibo(x):
# 작은 곳에서 큰 곳으로 가는 상향식
for i in range(1, x+1):
if i == 1 or i == 2:
dp[i] = 1
else :
dp[i] = dp[i-1] + dp[i-2]
return dp[x]동적 프로그래밍 문제에 접근하는 방법
- 가장 먼저 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 해결할 수 있는지 검토한다.
- 이 때, 다른 아이디어로 해결이 안될 것 같거나 시간이 너무 오래 걸릴 것 같을 때 동적 프로그래밍을 고려해본다.
- 일단, 재귀함수로 비효율적인 완전 탐색 프로그램을 작성(하향식)한 후 코드를 개선해가는 방향으로 생각해도 된다.
이런 개념을 갖고 문제에 도전해보자 !