210104 개발일지(28일차) - 유명한 DP 알고리즘 문제 : 냅색(knapsack) 알고리즘(feat. 백준 12865번)

오늘은 0-1knapsack 알고리즘에 대해서만 알아보자!
아마, 분할가능(Fractional) 냅색 알고리즘은 언젠가 포스팅할 날이 오겠지..

분할가능 냅색 알고리즘 vs 0-1냅색 알고리즘(분할 불가능)

심지어, 냅색 알고리즘은 담을 물건들이 나뉠 수 있느냐 없느냐에 따라 또 나뉘어진다.

1. 분할가능 냅색 알고리즘(Fractional knapsack algorithm) : 담을 수 있는 물건이 소금처럼 나누어질 때 사용하는 알고리즘
2. 0-1 냅색 알고리즘(0-1 knapsack algorithm) : 위의 문제처럼, 담을 수 있는 물건이 나누어지지 않을 때 사용하는 알고리즘

냅색(knapsack) 알고리즘

백준 문제를 캡쳐했다.
문제는 아래 나온 것처럼 간단해보이는데, DP문제의 일종으로 따로 알고리즘 이름이 있을 정도로 유명하고 생각보다 어려운 문제다.
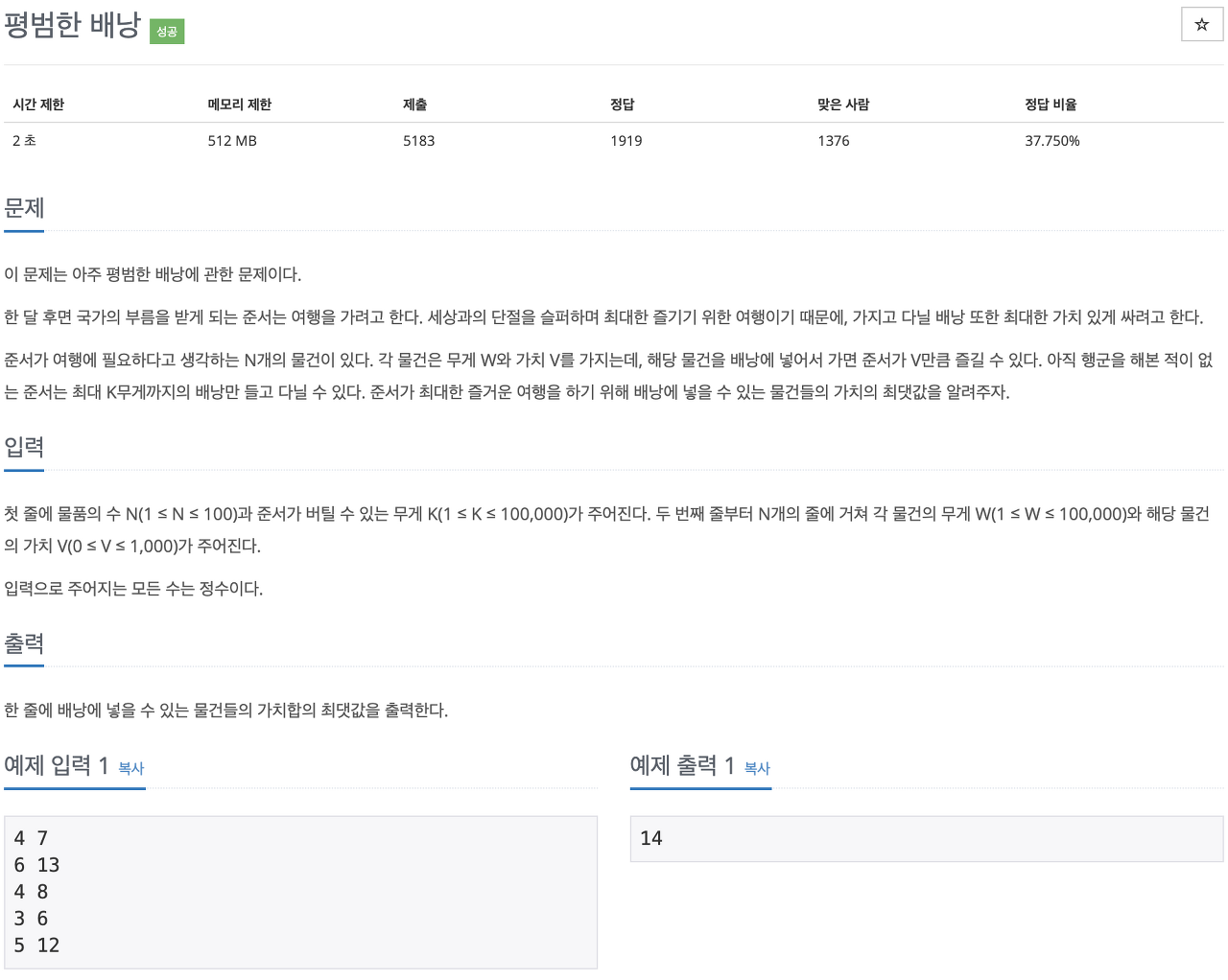요약하면, 배낭에 담을 수 있는 최대값이 정해져있고 특정 가치&무게가 있는 짐들을 배낭에 넣을 수 있다. 이 때, 가치들의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제다.

0-1냅색 알고리즘 말로 풀어보기

위에 설명했듯 분할할 수 없는 0-1냅색 알고리즘 풀이에 대해서 보자.
먼저, 말로 설명을 하고나서 표로 설명을 해보겠다.

1. knapsack이라는 행렬은 2차원 행렬로, 가로축에는 현재 가방 무게(최대 들 수 있는 무게)이며 세로축은 물건이이라고 생각하자. 이 때, knapsack행렬에서 답을 구하는 것이며 우리가 평소 생각하는 dp테이블이라고 생각하면 된다.
   (이 때, 테이블은 원래 dp문제 풀 듯이 0행에는 다 0을 넣어준다. 논리적으로도 아무 것도 안 넣으면 0이니까..)
2. 행(i)-열(j) 우선순으로 탐색한다. 탐색하며 집어 넣는 값은 물건의 가치이다.

3-1. 가방 무게보다 현재 물건이 무거우면, 위의 행에 있는 가치를 그대로 가져온다.
3-2. 그렇지 않으면(가방에 물건을 집어넣을 수 있으면), 비교해서 max값을 가져온다.
비교 대상은, '위의 행에 있는 가치' vs '지금 물건의 가치 + (현재 가방 무게-물건의 무게)에서 넣을 수 있는 물건의 가치'이다.
4. 이렇게 채운 knapsack 행렬에서 가장 마지막 값을 가져오면 답이다.

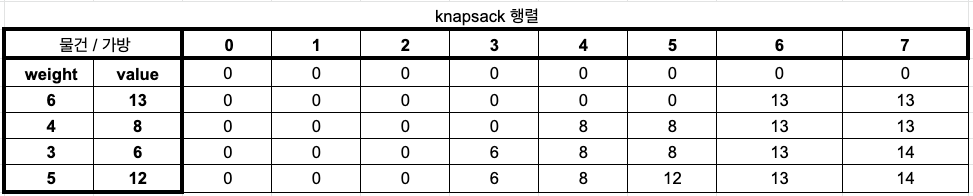
0-1냅색 알고리즘 표로 풀어보기

1행 1열부터 채워진다고 생각하자.
위에 말로 푼 내용에서 3-1, 3-2를 열심히 활용하면 아래와 같이 표를 채울 수 있다.

0-1냅색 알고리즘 코드화 하기(파이썬)

import sys
# N은 물건의 갯수, K는 가방 무게 최대값이다.
N, K = map(int, input().split())
stuff = [[0,0]]
knapsack = [[0 for _ in range(K + 1)] for _ in range(N + 1)]

for _ in range(N):
    stuff.append(list(map(int, input().split())))

#냅색 문제 풀이
for i in range(1, N + 1):
    for j in range(1, K + 1):
        weight = stuff[i][0] 
        value = stuff[i][1]
       
        if j < weight:
            knapsack[i][j] = knapsack[i - 1][j] #weight보다 작으면 위의 값을 그대로 가져온다
        else:
            knapsack[i][j] = max(value + knapsack[i - 1][j - weight], knapsack[i - 1][j])

print(knapsack[N][K])