DP 알고리즘 공부하면서, 이해 못하는 부분들이 꽤 많았는데.. 이건 정말 힘들다.
아직도 완벽히 이해 못했지만, 일단 이해하는 데까지 포스팅을 해 볼 생각이다. 훗날 완벽히 이해한 날이 왔을 때, 추가설명을 하면 너무 뿌듯할 것 같다. (미래의 나 파이팅)
어떤 분의 블로그에 정말 자세히도 설명히 돼있다. 이 분 정보와 승이의 설명이 큰 도움이 됐는데, 아직 완벽한 이해는 아니다..
외판원문제 대표유형(feat.백준 2098번)
아래와 같이 1~N번 도시가 있을 때, 어느 한 도시에서 출발해서 나머지 도시들을 다 거쳐 돌아올 때 최소비용을 구하는 문제다.
핵심 아이디어
- 출발지는 중요하지 않다.
- 다시 돌아와야 하기 때문에, 어디 지점을 출발지로 잡든 간에 상관없다.
(출처 : https://red-pulse.tistory.com/29)
- dfs로 전체를 순회하면서 값을 저장하면, 되겠지만.. 시간복잡도가 O(n!)이 되어 너무 크다.
→ 어떻게 줄일 수 있을까 생각하면, 아래와 같이 겹치는 부분이 생기는 점을 catch하고 DP 알고리즘 활용할 생각을 해야한다.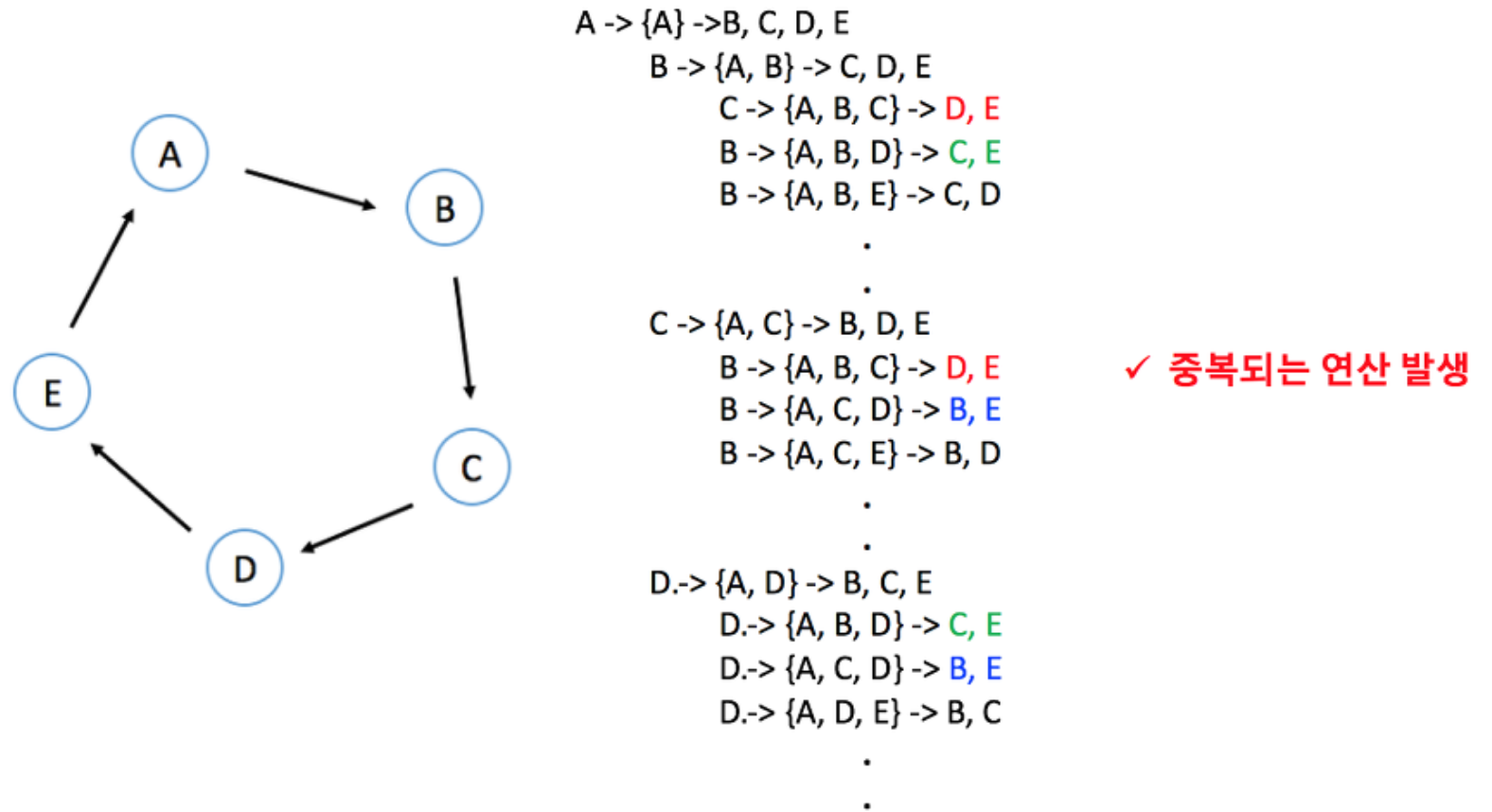
비트마스크 개념
이 문제를 풀기 위해 비트마스크 개념을 도입하면 조금 더 편하게 생각할 수 있다.
예를 들면, A~E 도시를 순환하는데 현재 D도시에 있으며 A,C,D 도시를 방문한 상태라면 '10110'로 표시하는 개념이다.
- 조금 더 알아보기 : https://kim6394.tistory.com/246
파이썬 코드
이제 위의 개념들을 가지고 재귀함수를 이용해서 풀면 된다.
아직 제대로 직접 짠 코드는 없고, 승민이가 짜준 코드만 있다.. 여기 주석을 달았다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10000)
INF = float('inf')
n = int(input())
mat = [list(map(int, input().split()))for _ in range(n)]
dp = [[INF]*(1 << n)for _ in range(n)]
def dfs(current, visit):
if visit == (1 << n)-1: #재귀함수의 종료 조건이다. 비트마스크 활용하여, 전체 도시에 방문했을 때가 종료 조건이다.
if mat[current][0] == 0: #갈 수 없는 곳 : mat값이 0인 곳
return INF #그러면 inf를 리턴해라.
else:
return mat[current][0] #갈 수 있는 곳이면, 현재 위치(마지막 도시)에서 출발 지점으로 돌아가는 가치를 리턴해라.
if dp[current][visit] != INF: #방문한 적이 있다면
return dp[current][visit] #그 값을 리턴하라.
for i in range(n):
if not visit & (1 << i) and mat[current][i] != 0: #방문한 적이 없고, 갈 수 있는 도시라면
dp[current][visit] = min(dp[current][visit], dfs(i, visit | (1 << i))+mat[current][i]) #기존의 값 vs 재귀함수 안에서 받은 값+현재 가치를 더한 값을 비교해서 최소값을 받아라.
return dp[current][visit]
print(dfs(0,1))