[cs231n] Lecture 6 : Training Neural Networks, Part 1

6차시 - 인공신경망 학습 파트 1

Part 1에서는 다음과 같은 것들을 배웠다.

• Activation Functions (활성화함수)
• Data Preprocessing (데이터전처리)
• Weight Initialization (가중치 초기화)
• Batch Normalization (배치 정규화)
• Babysitting the Learning Process (학습과정 다루기)
• Hyperparameter Optimization (하이퍼파라미터)

1. Activtion Functions(활성화함수)

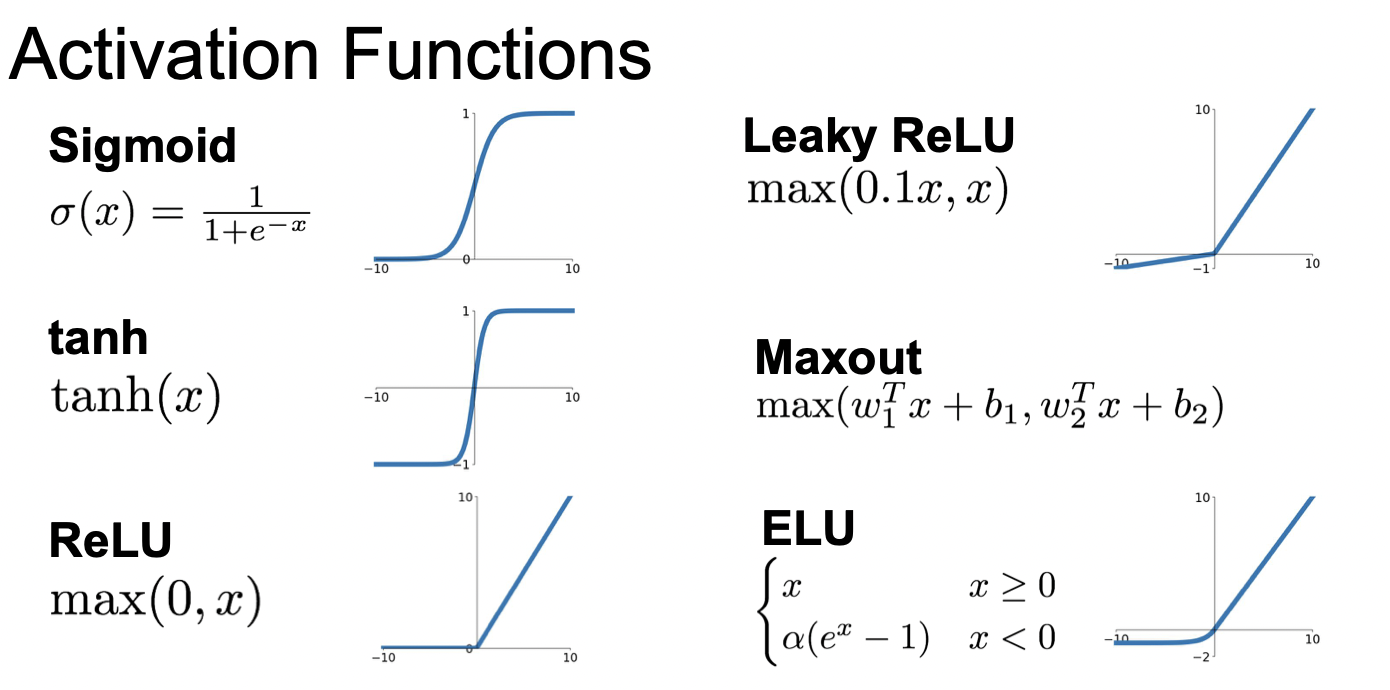
데이터 입력이 들어오면 가중치와 곱하고(FC 또는 CNN), 그 다음 활성화함수, 즉 비선형 연산을 거치게 된다. 활성화 함수에는 여러가지 종류들이 있다.

시그모이드 함수는 뉴런의 "firing rate"를 saturating 시킨다.
어떤 값이 0과 1사이의 값을 가지면 이를 "firing rate"라고 생각할 수 있으며, "Saturated"는 0으로 수렴해서 정보를 잃어버리는 것을 말한다.

시그모이드 함수는 문제점이 몇 가지 있는데, 1) Saturated 뉴런들이 기울기를 죽인다는 것이며, 2) Zero-centered 되지 않았다이며, 3) exp() 하는 계산의 비용이 많이 든다는 것이다.

Saturated 뉴런들이 기울기를 죽인다는 것을 설명하자면 다음과 같다.
x = 10일때, x = -10일때 보면 쉽게 기울기가 0이라는 것을 알 수 있다. 이처럼 양이든 음이든 일정한 크기를 가진 X의 기울기는 0이다. 그리고 기울기가 0이게 되면 Backprop를 할 때 0인 값을 전달하게 되어 더 이상 기울기를 전달 하지 못하게 된다.

참고: https://hyen4110.tistory.com/14

sigmoid를 통과하게 되면 양수만 나오게 된다. 즉, 뉴런의 입력값이 항상 양수이다. 이는 오차역전파를 이용하여 가중치를 학습할 때 효율적이지 못하다.

$\frac{dL}{dW}$ = $\frac{dL}{df}$$\frac{df}{dW}$ 인데, f=wx+b이므로 미분하면 $\frac{df}{dW}$은 X이다. 여기서 X값들이 전부 양수이면, $\frac{dL}{dW}$와 $\frac{dL}{df}$의 부호는 같다. 즉 처음 손실함수의 부호를 그대로 가중치가 학습되게 된다.

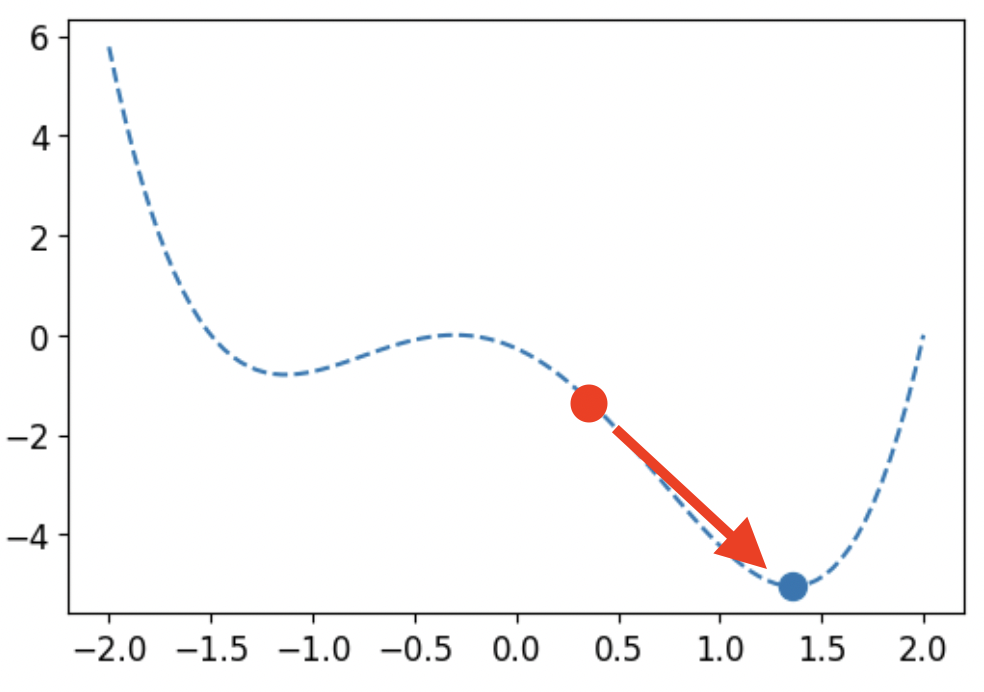
현재 빨간점에 위치한다면, 파란점에 가려면 화살표 방향대로 이동해야 된다. 그래프의 y 값은 J(θ)이며, x값은 θ이다. 여기에서 θ은 네트워크 파라미터이다.
loss를 줄이기 위해 기울기의 반대 방향대로 한 스텝 간다.
업데이트 되는 값을 +해서 표현한다면, $θ^+$ = θ - α$\frac{dJ}{dθ}$이고, $w^+$ = $w$ - α$\frac{dJ}{dw}$이다. 하지만 sigmoid를 사용한다면 $\frac{dJ}{dw}$와 $\frac{dJ}{dθ}$의 부호가 같다. 따라서 지그재그로 움직이게 되어 비효율적이게 된다.

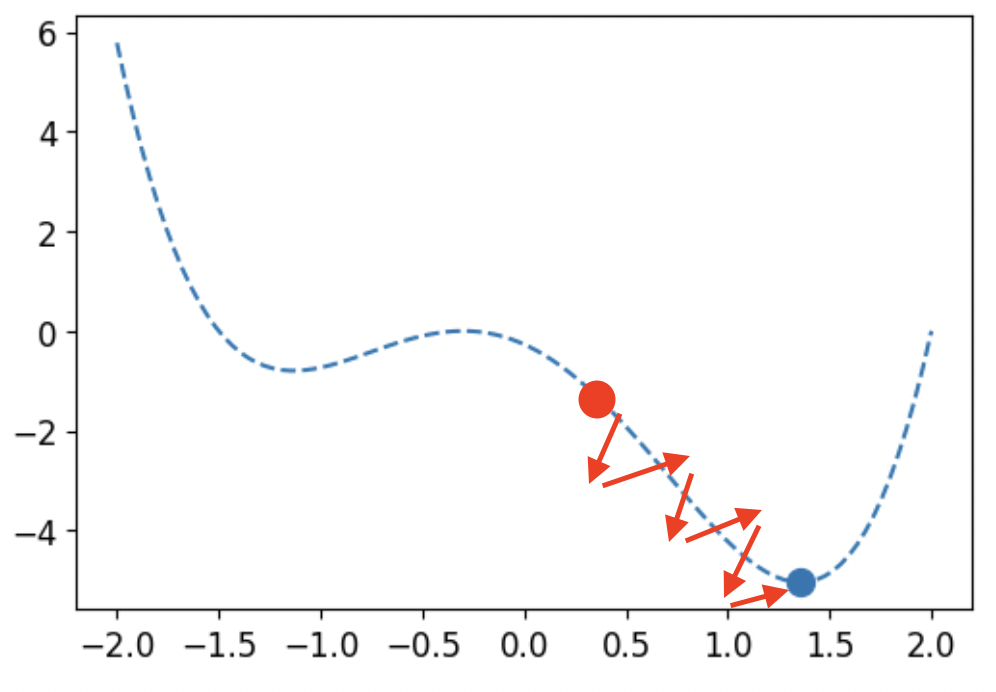
참고: https://codetorial.net/articles/univariate_convex_function_optimization.html

sigmoid 함수 외에 하이퍼볼릭탄젠트 함수가 있다. 범위가 -1부터 1까지이어서 항상 양수만 출력해서 생기는 비효율적으로 진행되는 문제를 해결한다. 하지만 여전히 포화되는 문제는 있다.

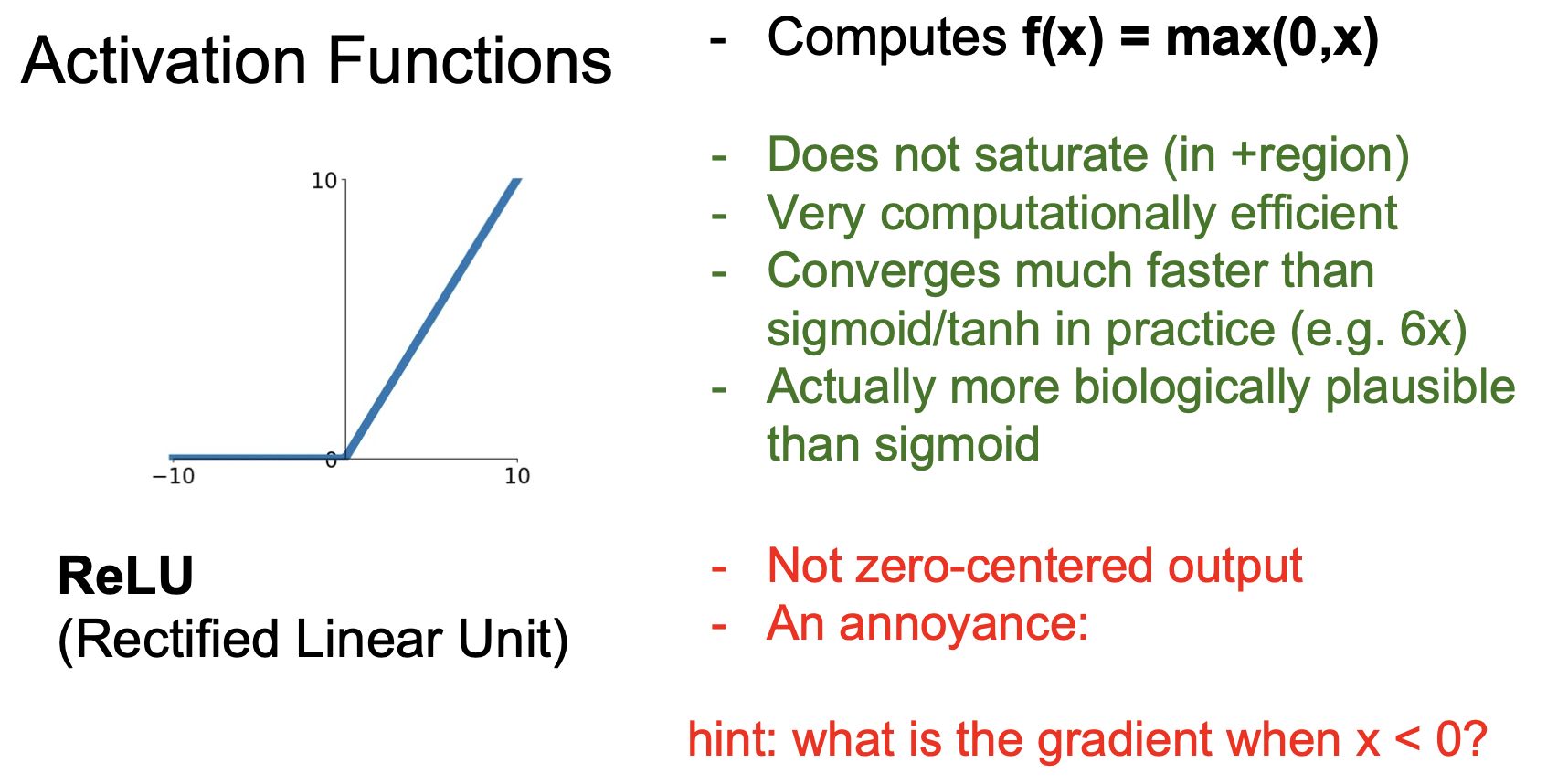
0 이상의 입력에 대해서는 포화되지 않으며, 전에 봤던 함수들보다 빠르다. 하지만 계속 0을 출력하는 죽은 뉴런이 발생하면 학습이 진행되지 않는 문제점과 항상 양수만 출력하기 때문에 학습 속도가 더디다는 문제를 가지고 있다.


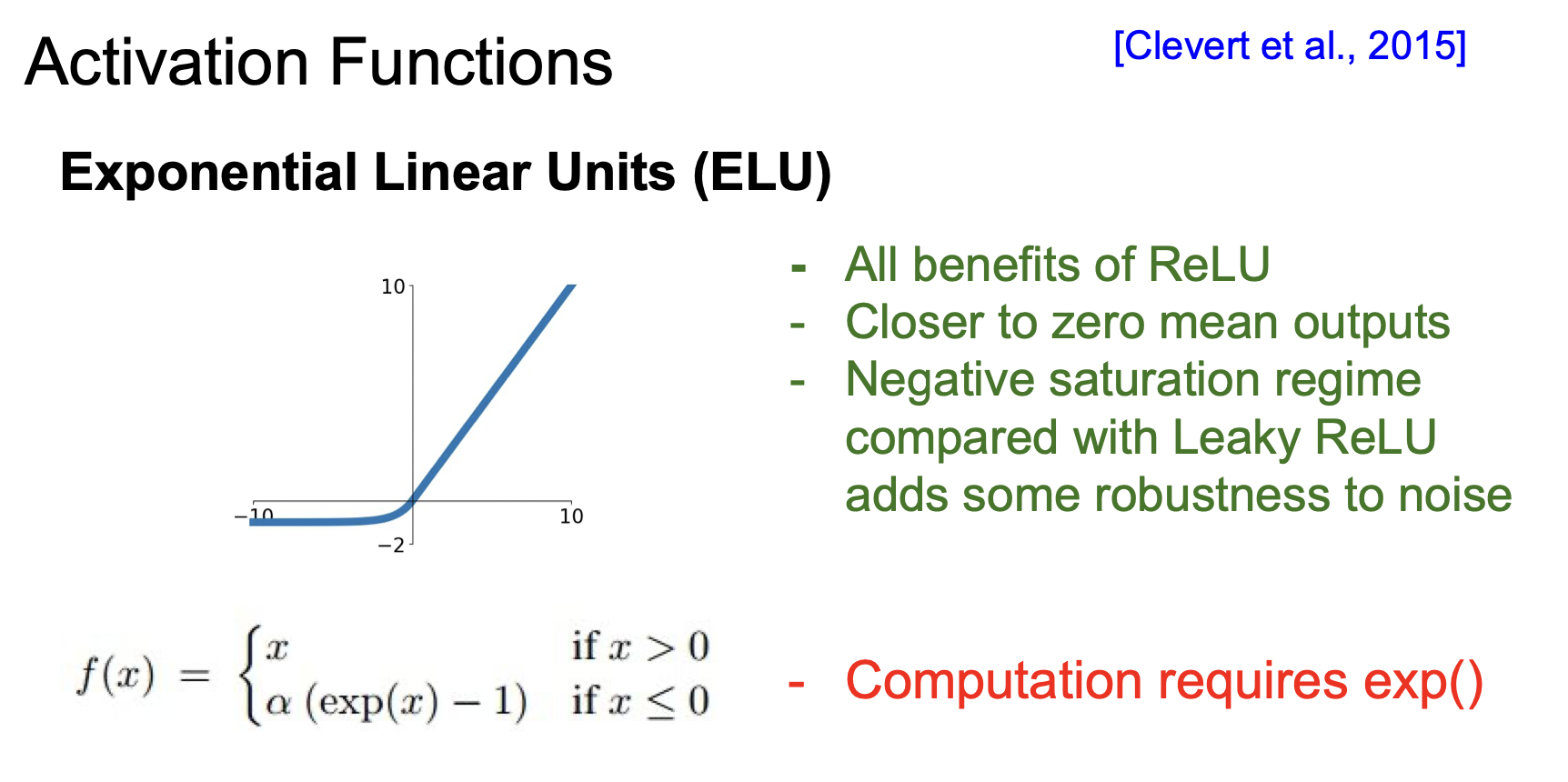
죽은 뉴런의 문제를 해결하기 위해, Leaky ReLU와 ELU가 등장했다.

Maxout은 활성 함수를 구간 선형 함수로 가정하고, 각 뉴런에 최적화된 활성 함수를 학습을 통해 나타낸다. 뉴런별로 선형 함수를 여러 개 학습해서 최댓값을 구하는 방식이다. Maxout은 선형 함수이기 때문에 포화되지도 않고, gradient가 죽지 않는다. 이렇게 성능이 뛰어나지만 두 개의 선형 함수를 비교한다면, 파라미터가 두 개가 된다는 문제점이 있다.

2. Data Preprocessing

위에서 시그모이드 함수를 설명할 때 입력이 모두 양수이게 되면 생기는 문제점에 대해 살펴보았다. 데이터 또한 같은 이유로 zero-centering 해줘야 한다.

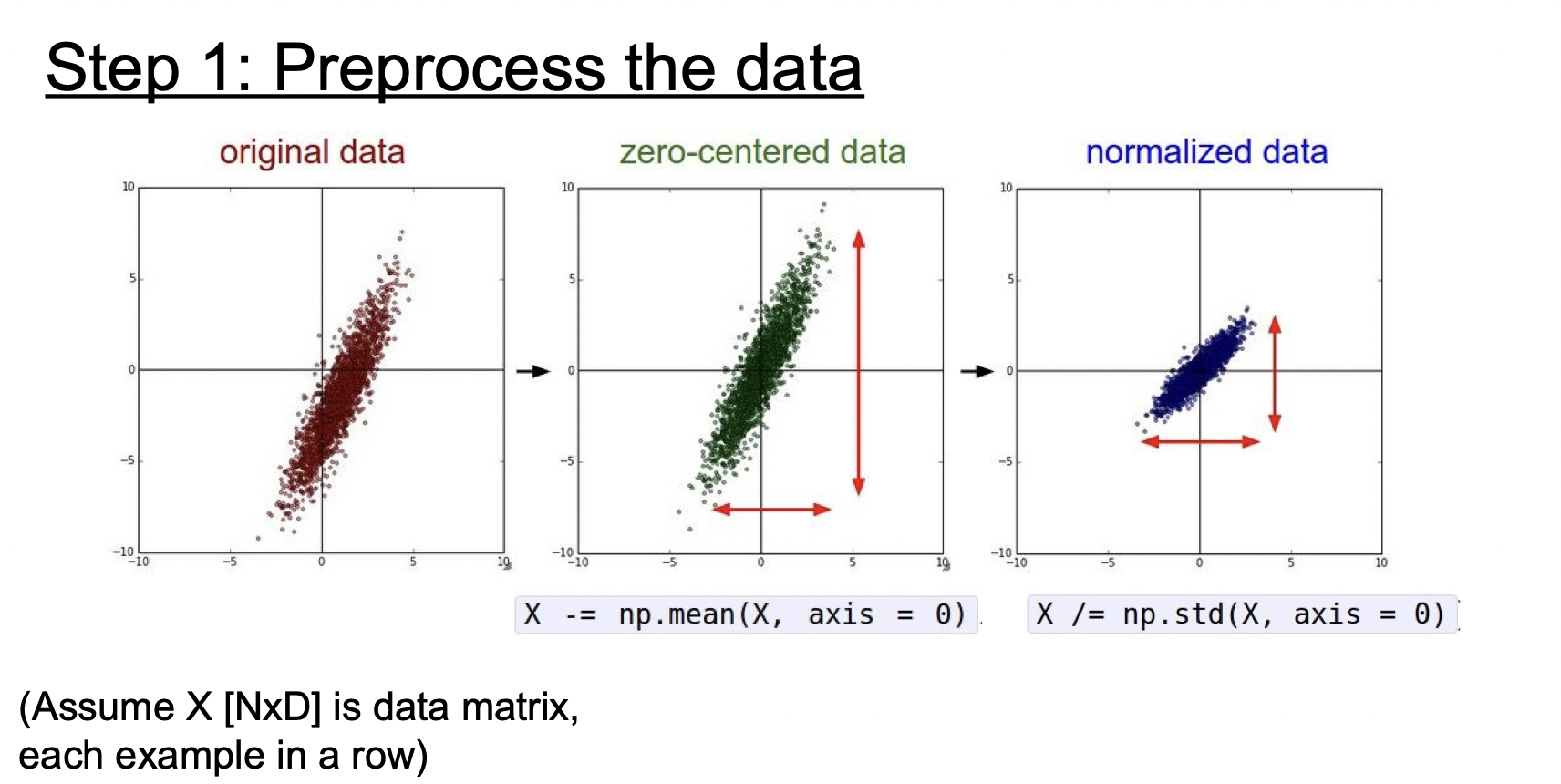
기존의 데이터를 zero-centering 하고 정규화하는 것이 일반적이다. 하지만 이미지는 이미 각 차원간에 스케일이 어느 정도 맞춰져 있기 때문에 정규화는 생략하는 경우가 많다.

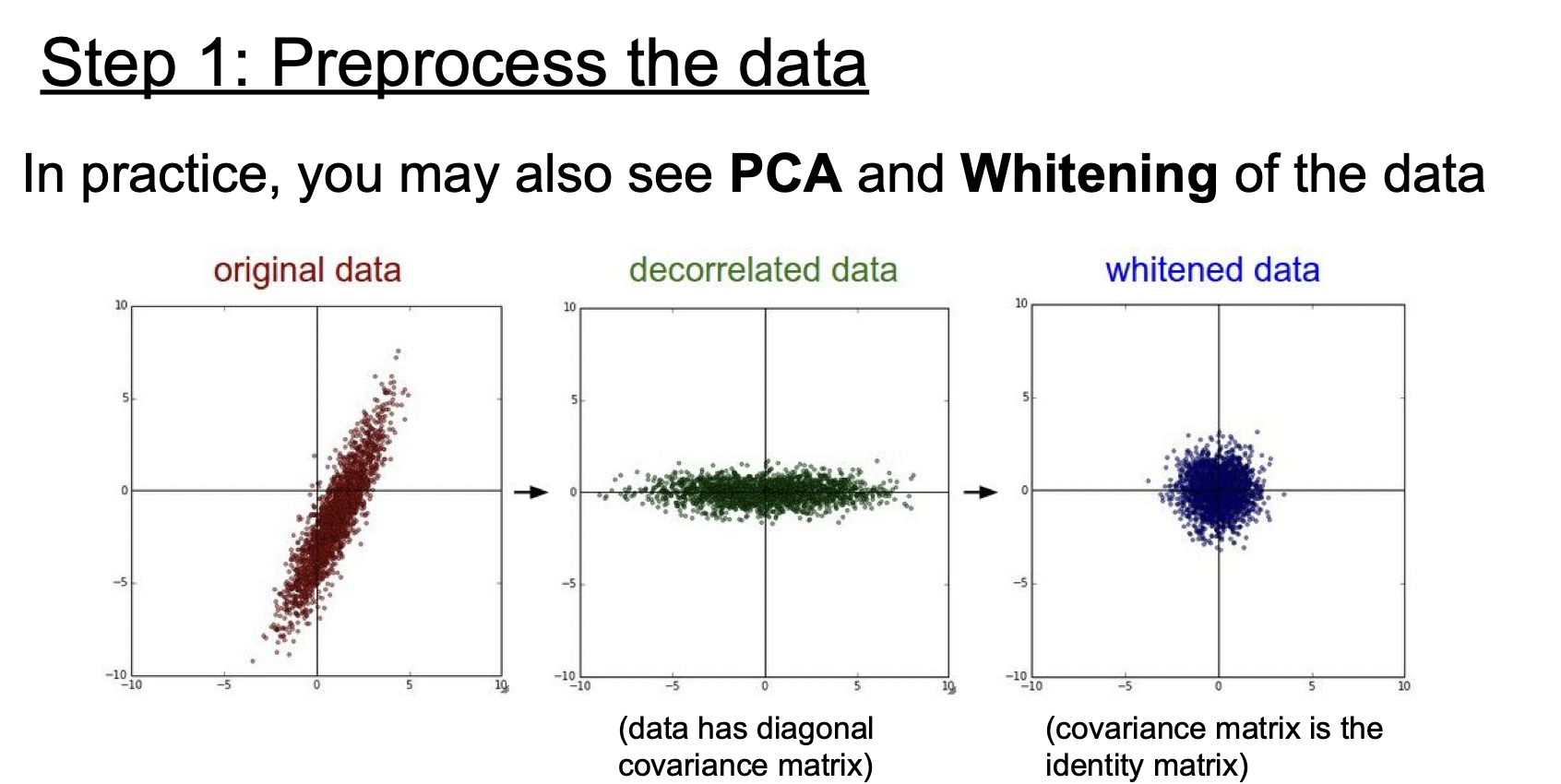
PCA와 Whitening도 있다.

이미지는 zero-centering만 하는 경우가 많은데, 모든 값의 평균을 구하는 경우와 각 채널 별로 평균을 구해서 적용하는 방식이 있다.

2. Weight Initialization(가중치 초기화)

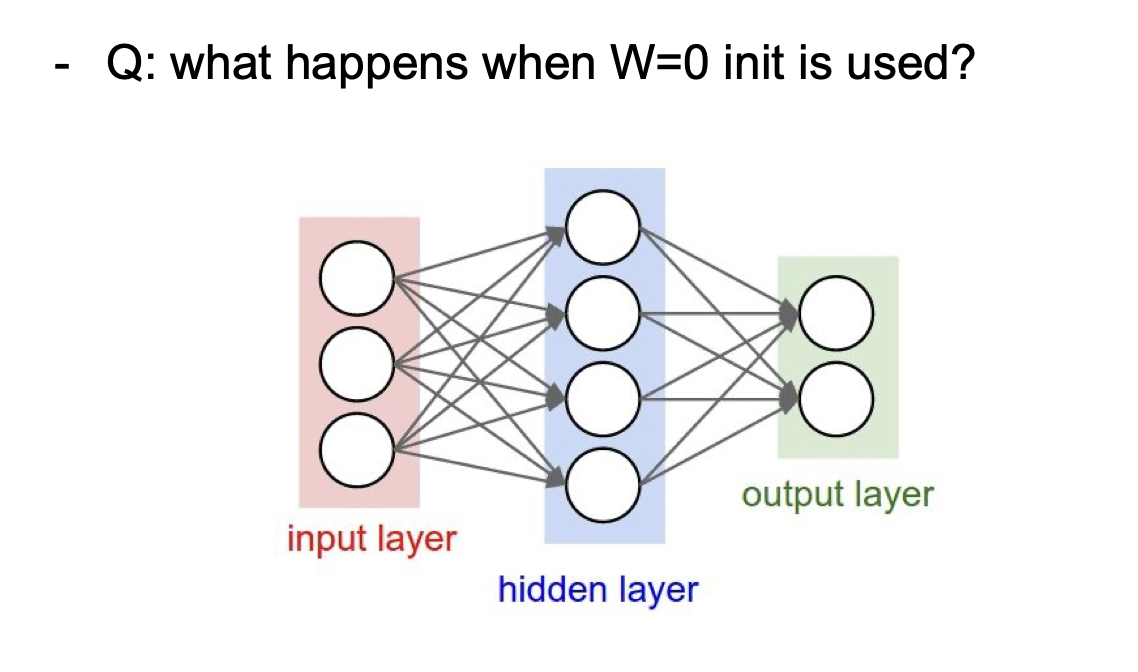
먼저 가중치들을 다 0으로 만드는 방법을 생각해 볼 수 있다. 하지만 가중치들이 모두 0이라면, 출력값들이 모두 같아지게 되므로 문제가 생긴다.

그 다음 생각은 작은 랜덤 숫자들로 초기화해주는 것이다. 초기 값을 표준정규분포에서 샘플링하는데 스케일을 더 작게 해주기 위해 0.01을 곱해준다.
작은 네트워크에서는 잘 작동하지만, 깊은 네트워크에서 문제가 발생한다.

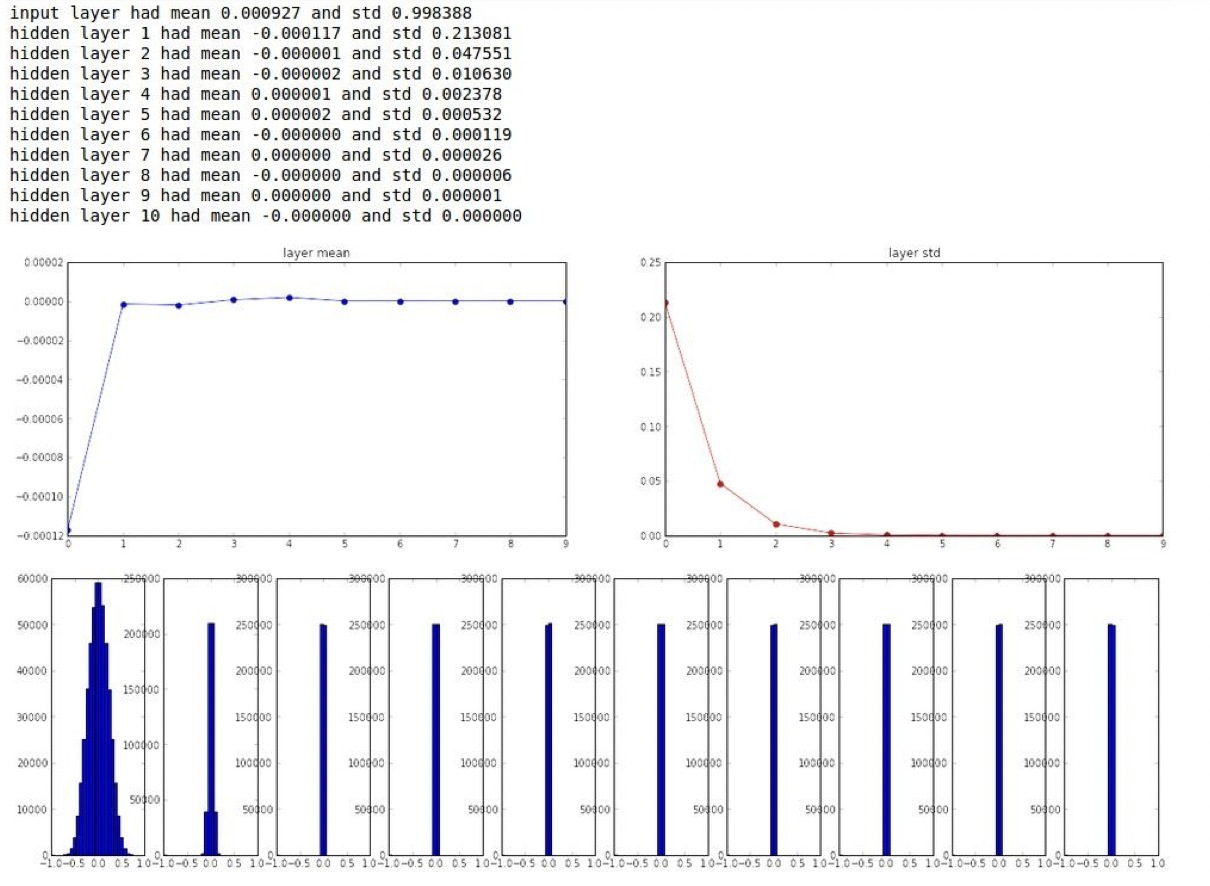
500개의 뉴런이 10개의 레이어로 구성된 모델이고 활성화함수로 하이퍼볼릭탄젠트함수를 사용한다. 하이퍼볼릭탄젠트가 zero-centered 함수이므로 평균은 0으로 수렴하고, 표준편차가 레이어를 지날수록 지나치게 작아진다는 것을 알 수 있다.
backward pass를 할 때도 비슷한 결과가 나올 것이다. backward의 과정을 보면 upstream gradient에 local gradient를 곱하는 건데, wx+b를 w로 미분하면 x가 나오고 x는 0에 가까운 아주 작은 값이기 때문에 계속 backward pass를 할수록 0에 가까운 작은 값이 나올 것이다.

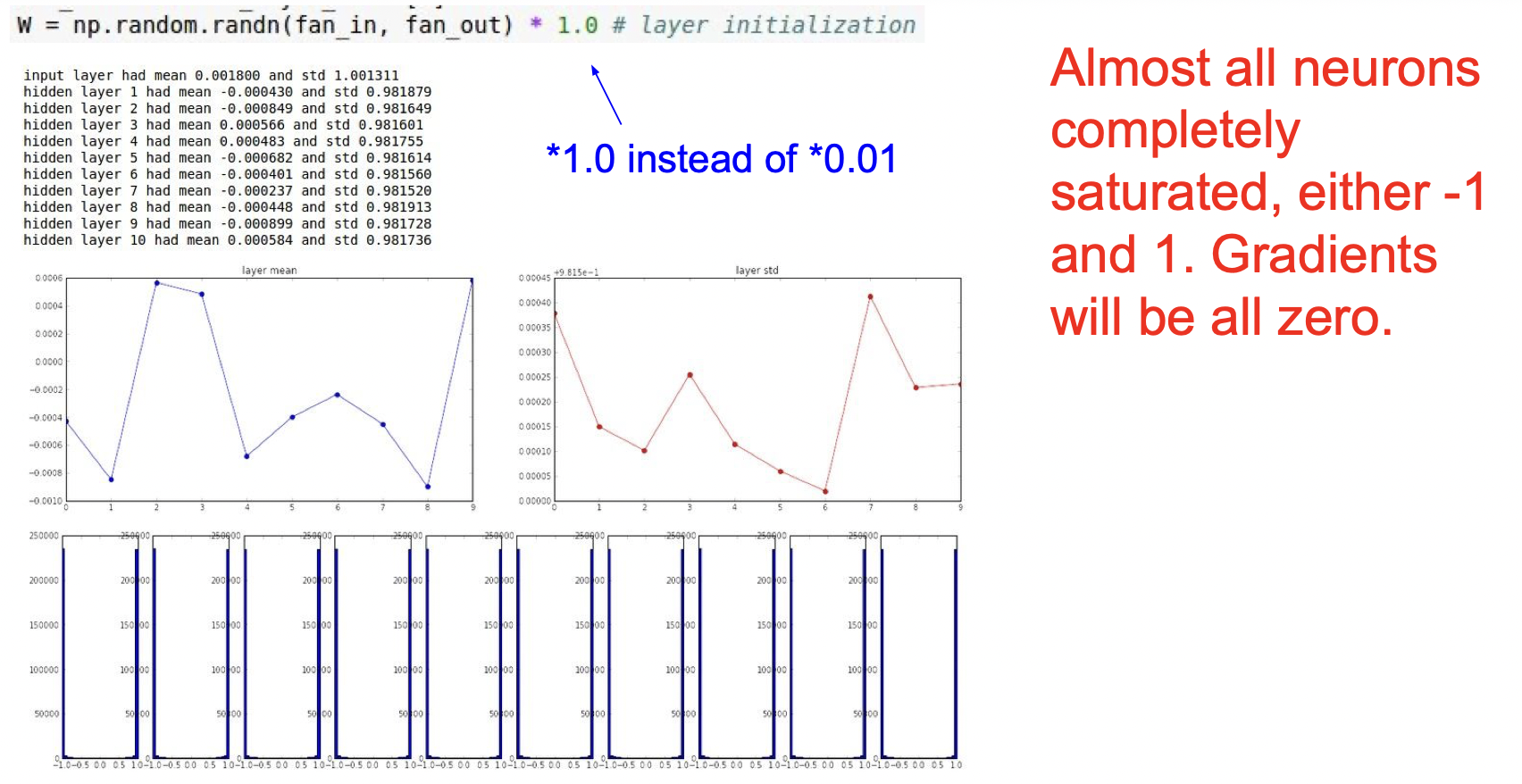
만약에 0.01대신 1을 곱해서 큰 값으로 가중치를 초기화한다면, 또 다른 문제가 발생한다. 하이퍼볼릭탄젠트함수를 거치면 -1또는 1로 수렴하기 때문에 모든 결과가 1또는 -1로 나오게 된다.

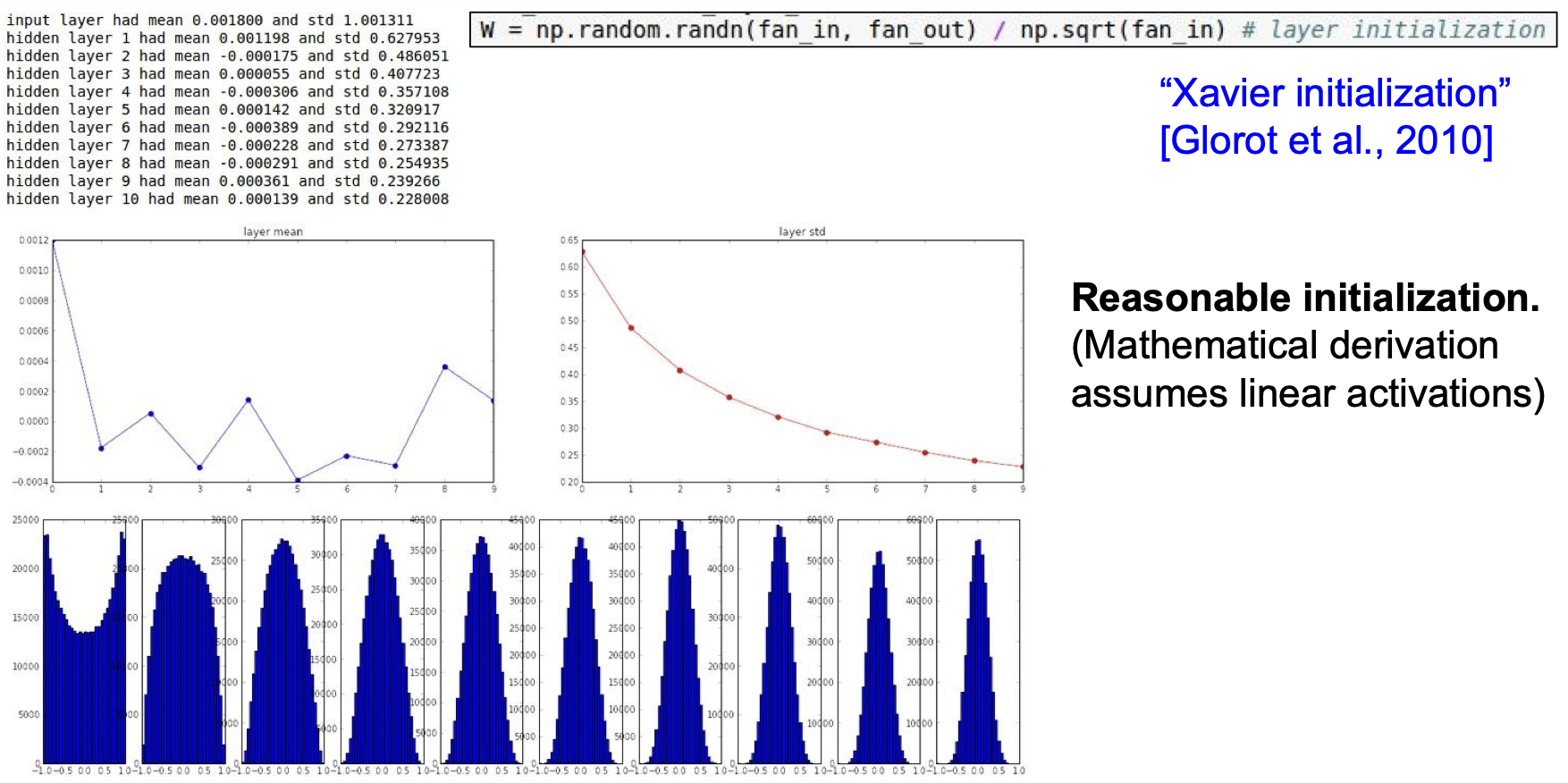
가중치를 초기화하는 것은 이처럼 중요한데 좋은 방법 중 하나가 Xavier initialization이다. Xavier initialization은 입/출력의 분산을 맞춰준다. 입력의 수가 적으면 더 작은 값으로 나눠서 큰 값이 나오도록 하는 방식이다.

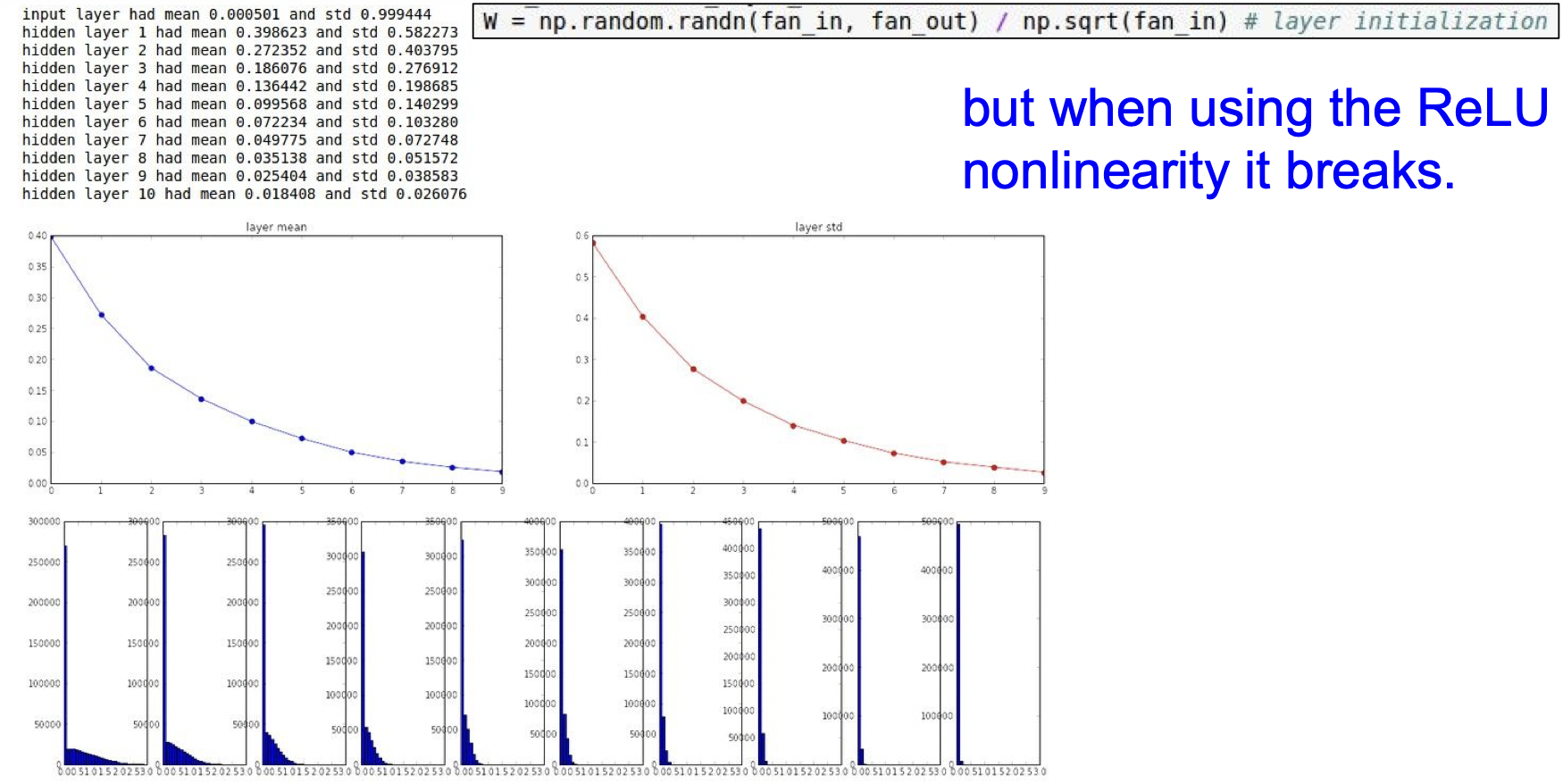
하지만 렐루함수에서는 잘 작동하지 않는 단점이 있다. 렐루함수는 절반이 죽어버려 분산도 절반이 되기 때문이다.

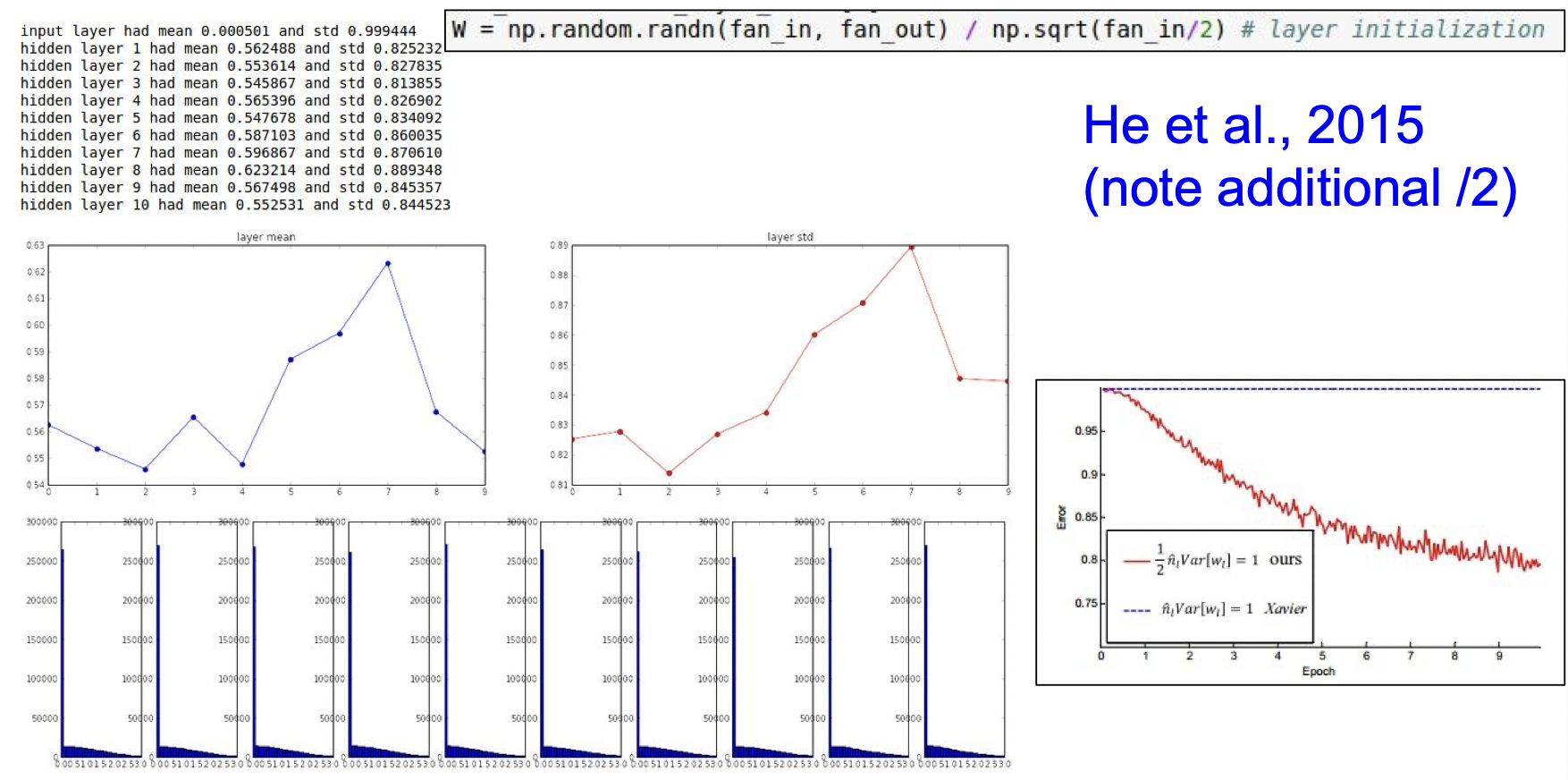
렐루에서는 추가적으로 2로 나눠주면 성능이 나아진다.

3. Batch Normalization(배치정규화)

배치 정규화는 가중치를 잘 초기화하는 것 대신에 학습할 때마다 모든 레이어가 각각 unit 가우시안 분포를 이루도록 하는 것이다. Batch 단위로 한 레이어에 들어오는 모든 값들의 평균과 분산을 구해서 가우시안 분포를 만드는 것이다.

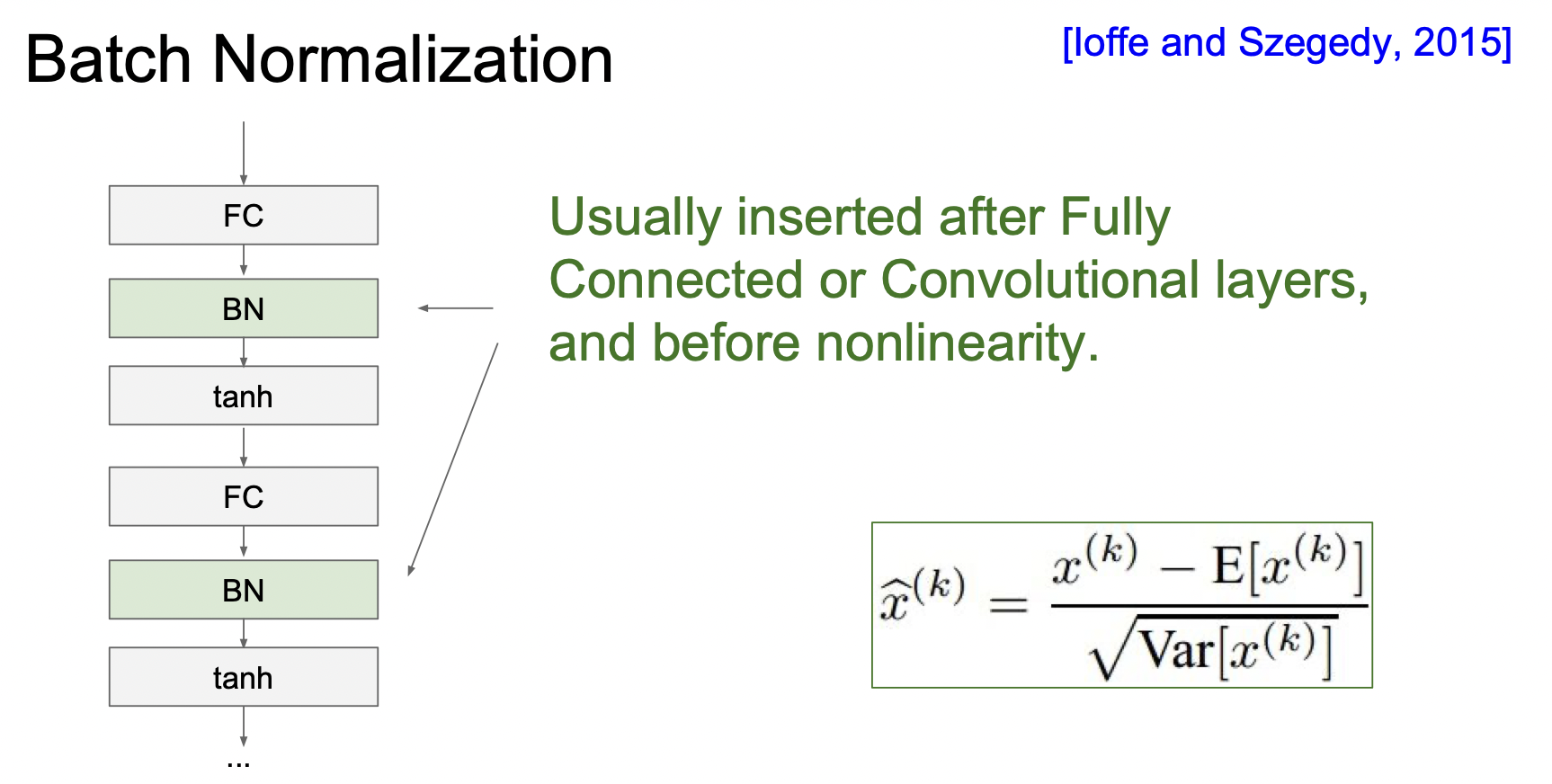
활성화함수 이전에 넣어줘서 포화되는 문제를 줄여준다. 입력의 스케일만 조정하는 것이기 때문에 FC, Conv에 다 적용 가능하다.
Conv에서는 차원마다 독립적으로 하는 것이 아니라 같은 Activation map의 같은 채널에 있는 요소들은 같이 정규화한다.

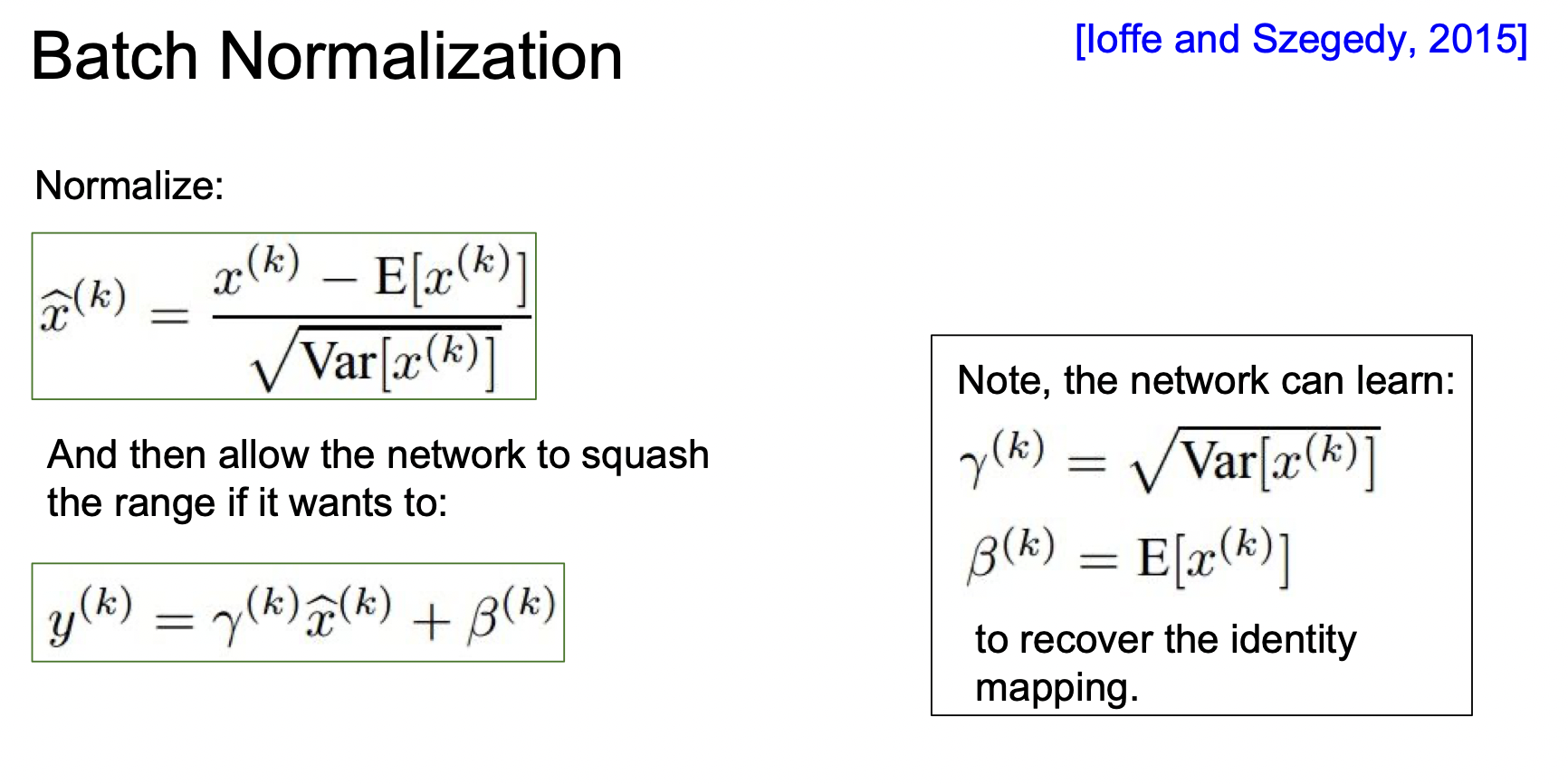
하지만 활성화함수에서 포화되지 않는 것이 마음에 들지 않다면, 배치정규화를 하기 이전으로 돌리는 계산도 있다. x에 분산을 곱하고 평균을 더해주면 된다.

4. Babysitting the Learning Process(학습과정 다루기)

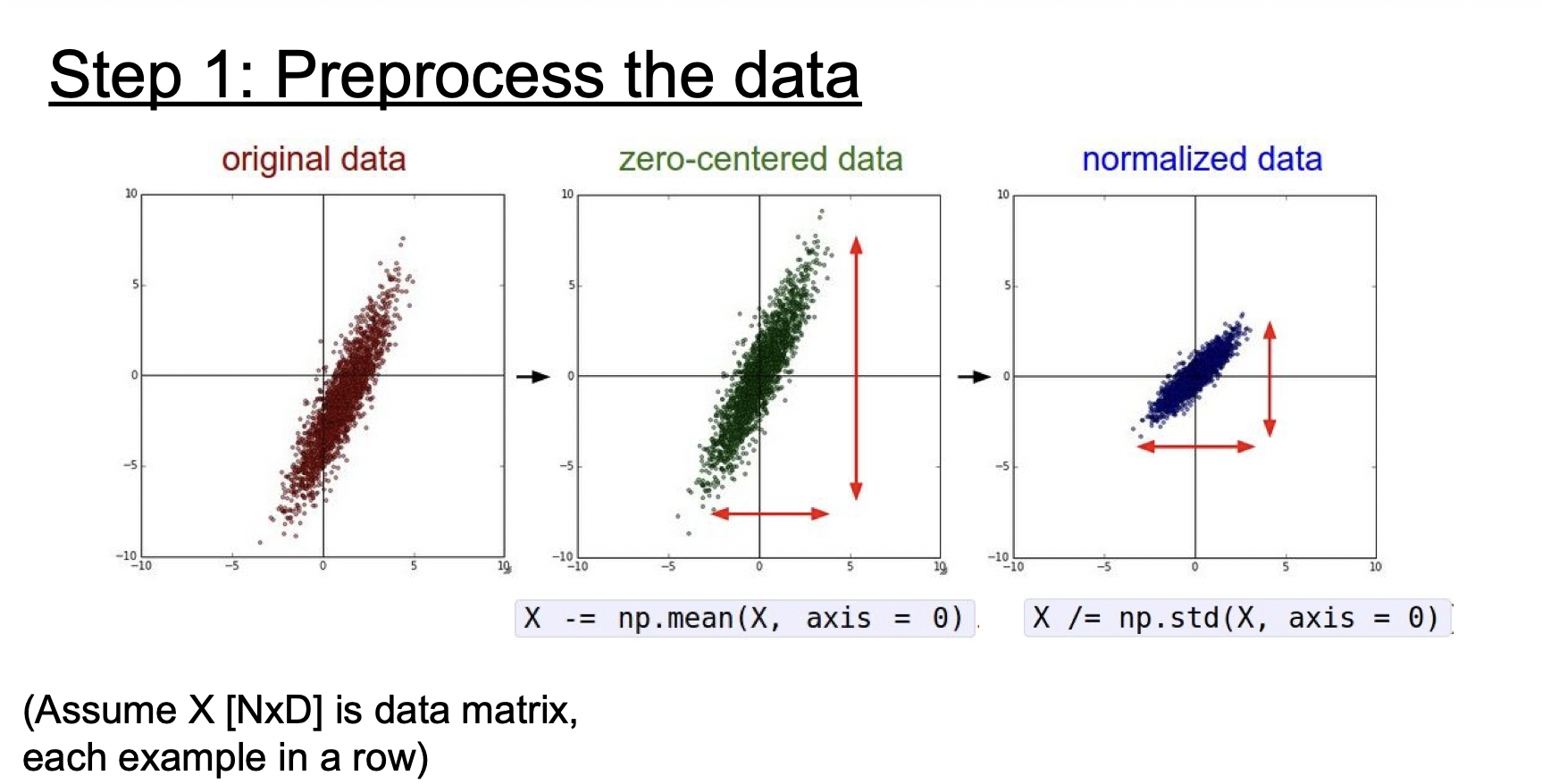
먼저 데이터전처리를 해준다.
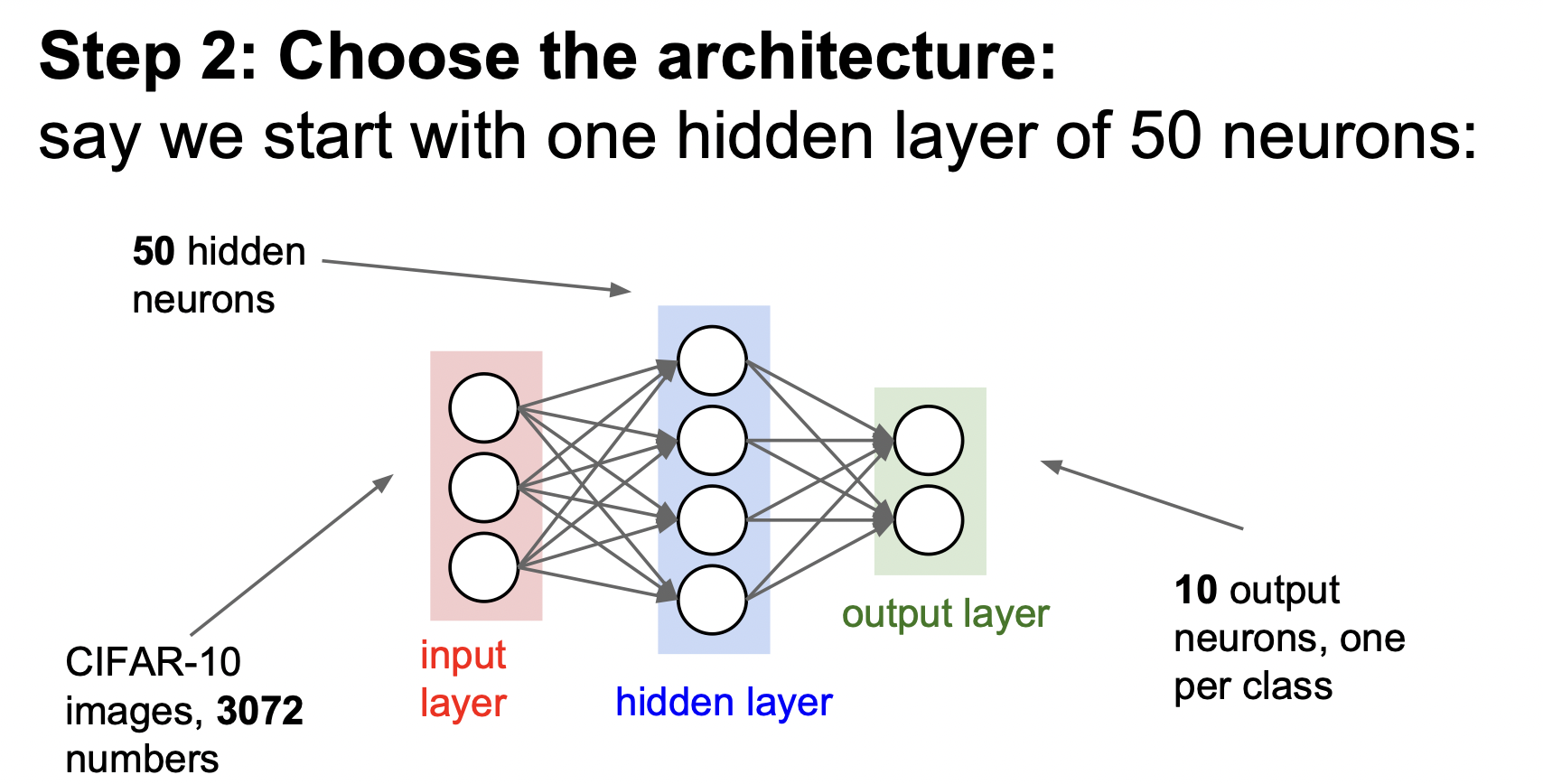다음으로는 모델을 설계한다.

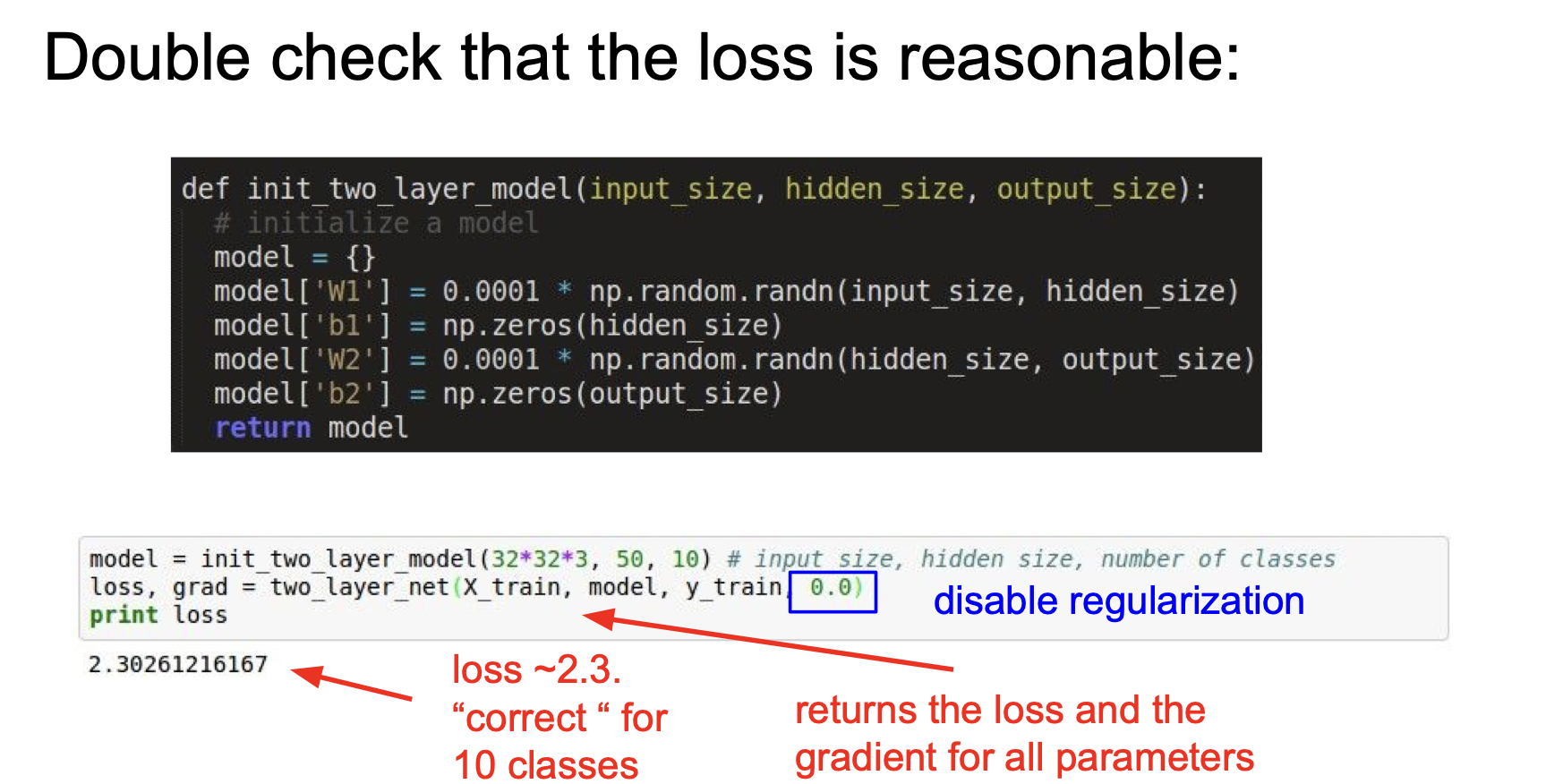
규제를 하지 않은 상태에서 loss가 괜찮게 나오는지 확인해본다. 소프트맥스에서 10개의 클래스를 적용하므로 2.3이면 적당하는 것을 알 수 있다.

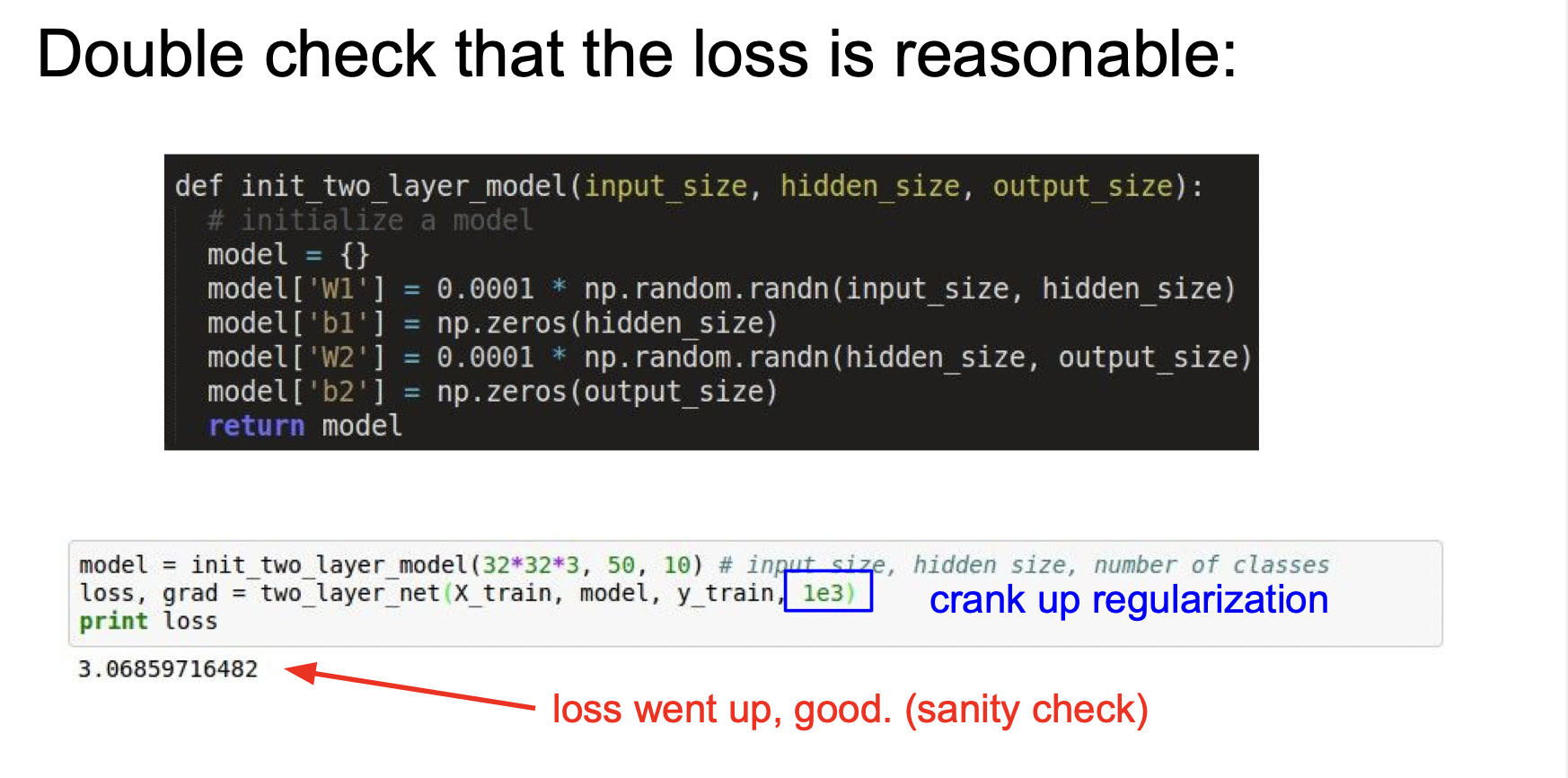
규제를 적용해보고 아까보다 loss가 더 커지기 때문에 제대로 작동한다는 것을 알 수 있다.

그 다음으로는 적당한 학습률을 정하면 된다. 학습률이 너무 작으면 loss가 너무 천천히 줄어들고, 너무 크면 발산하기 때문에 결과를 보면서 적당한 값으로 해주면 된다.

Hyperparameter Optimization(하이퍼파라미터 최적화)

Cross-validation strategy를 사용한다. Cross-validation은 Trainig set으로 학습하고, validation set으로 평가하는 방법이다. 넓은 범위를 살펴보고 점차 정교하게 범위를 설정한다.
정교하게 범위를 설정했을 때 좋은 값이 경계부분에 있다면, 다시 범위를 옮기는 것이 좋다. 즉 좋은 값이 중앙에 와야 범위를 제대로 설정한 것이다.

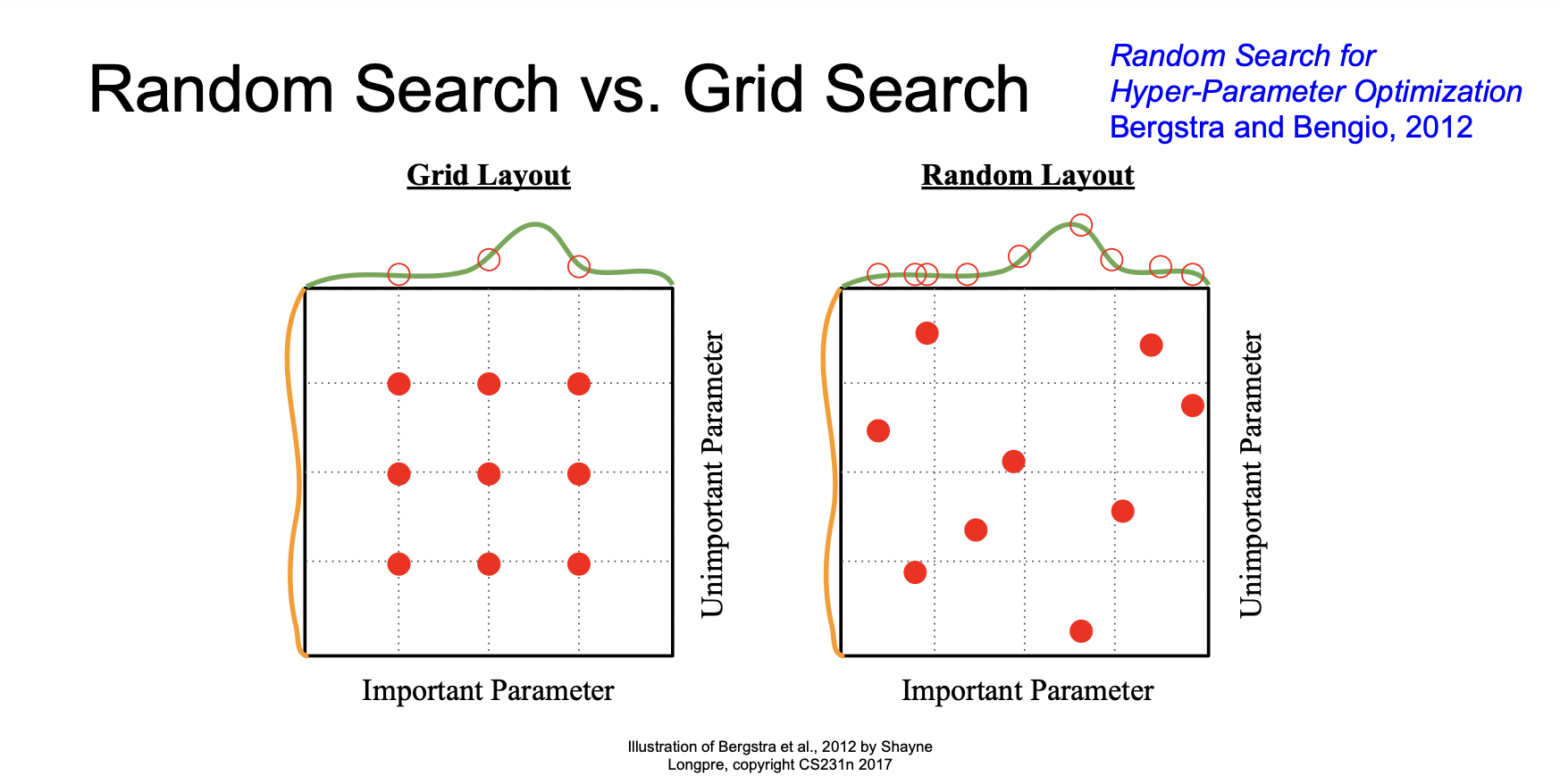
좋은 하이퍼파라미터를 찾기 위한 방법으로 Random Search와 Grid Search가 있다. Grid Search보다 Random Layout이 좋은 하이퍼파라미터를 찾기에 유리하다.

키워드 : Activation Functions(활성화함수), Sigmoid, Relu, Data Preprocessing(데이터전처리), normalization, PCA, Whitening, Weight Initialization(가중치 초기화), Xavier initialization, Batch Normalization(배치정규화), Babysitting the Learning Precess(학습과정 다루기), Hyperparameter Optimization(하이퍼파라미터 최적화), Random Search, Grid Search