5차시 - 컨볼루션 인공신경망
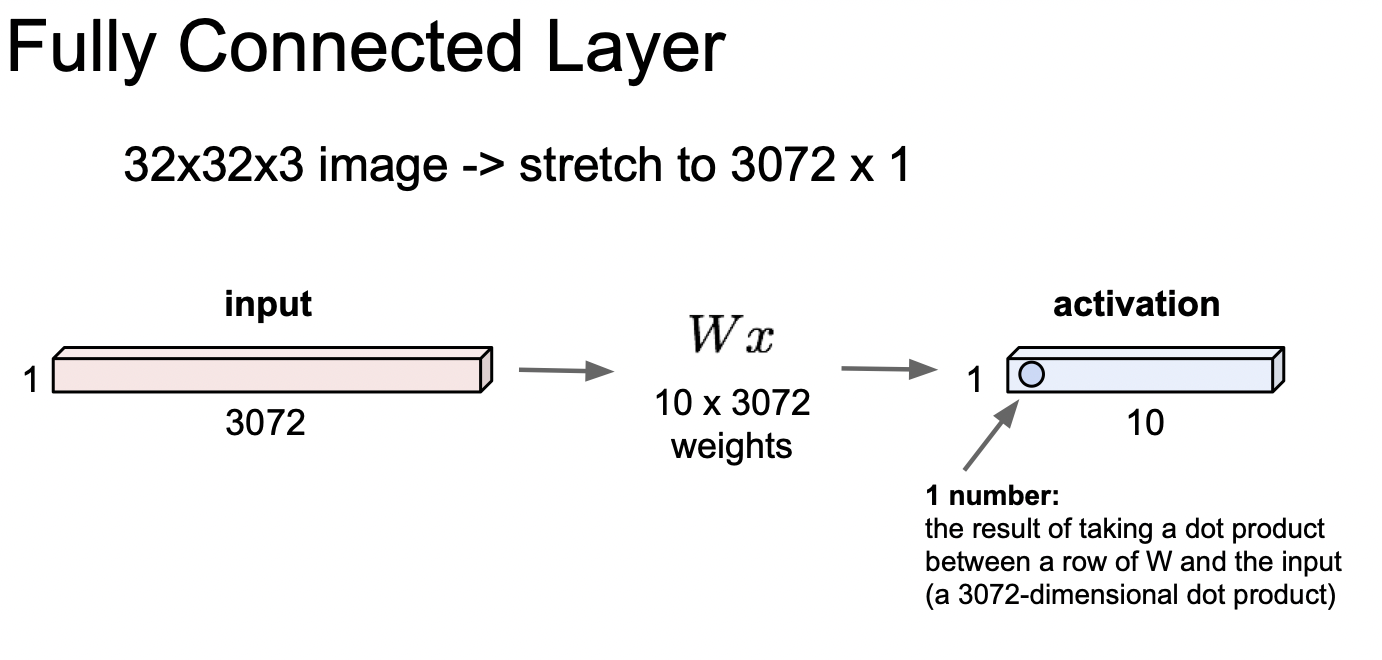
전차시에 배운 선형변환에서는 Fully Connected Layer를 사용한다. 열의 크기가 1인 행렬로 바꿔 준다음에 가중치와 행렬곱을 해주는데, 이는 한 줄로 펴주는 것과 같다.
위의 예시에서는 32x32x3인 이미지를 1차원 벡터로 피면 크기가 3072인 벡터이며, 크기가 10x3072인 가중치 행렬과 3072x1인 인풋 이미지를 곱해주면, 크기가 10x1인 행렬이 나온다.
Convolution Layer와 FC Layer의 가장 큰 차이점은 Convolution Layer은 기존의 구조를 보존한다는 것이다.
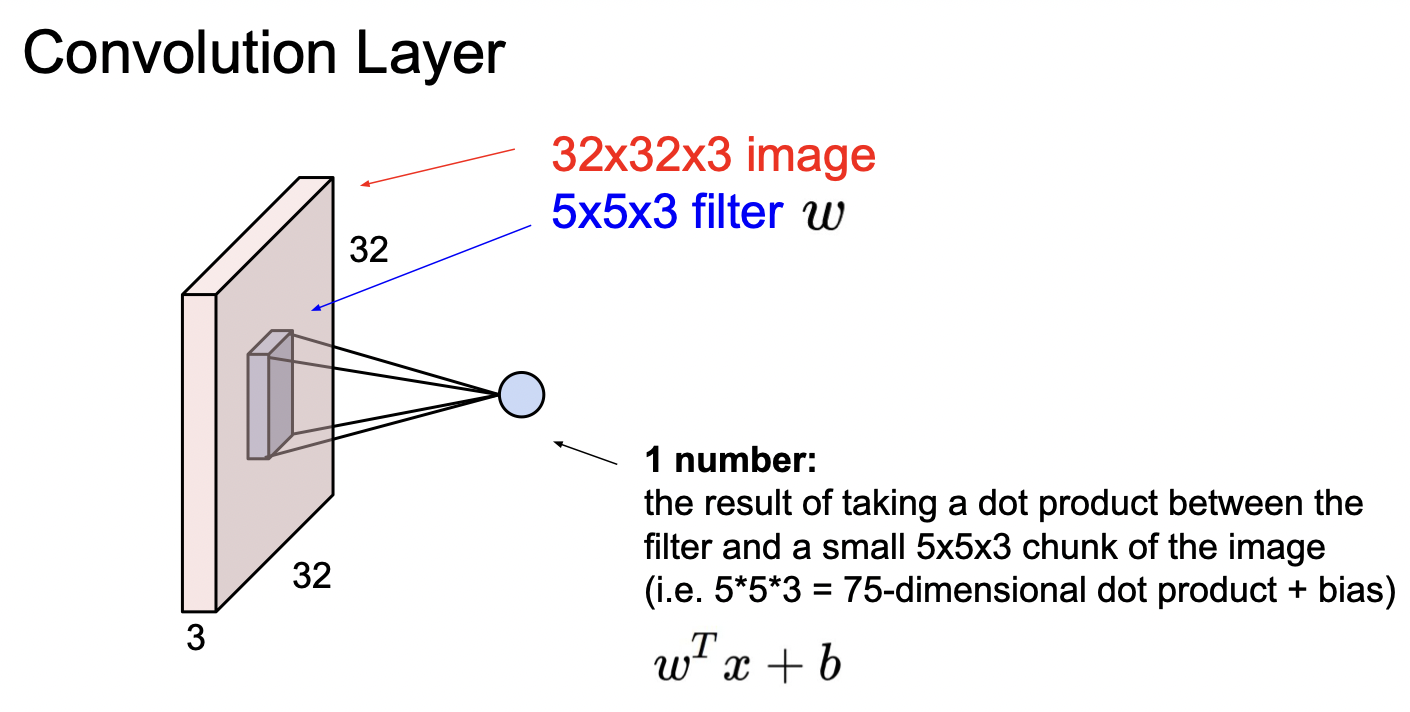
32x32x3인 이미지를 5x5x3인 필터가 이미지를 슬라이딩하면서 공간적으로 내적을 수행한다.
필터는 이미지의 깊이만큼의 깊이를 가지고 있어야 하며, 의 계산을 해준다. w가 transpose되는 이유는 벡터의 내적을 해주기 위해서이다. 쉽게 아까처럼 1차원 벡터로 펴준다고 생각하면 된다.
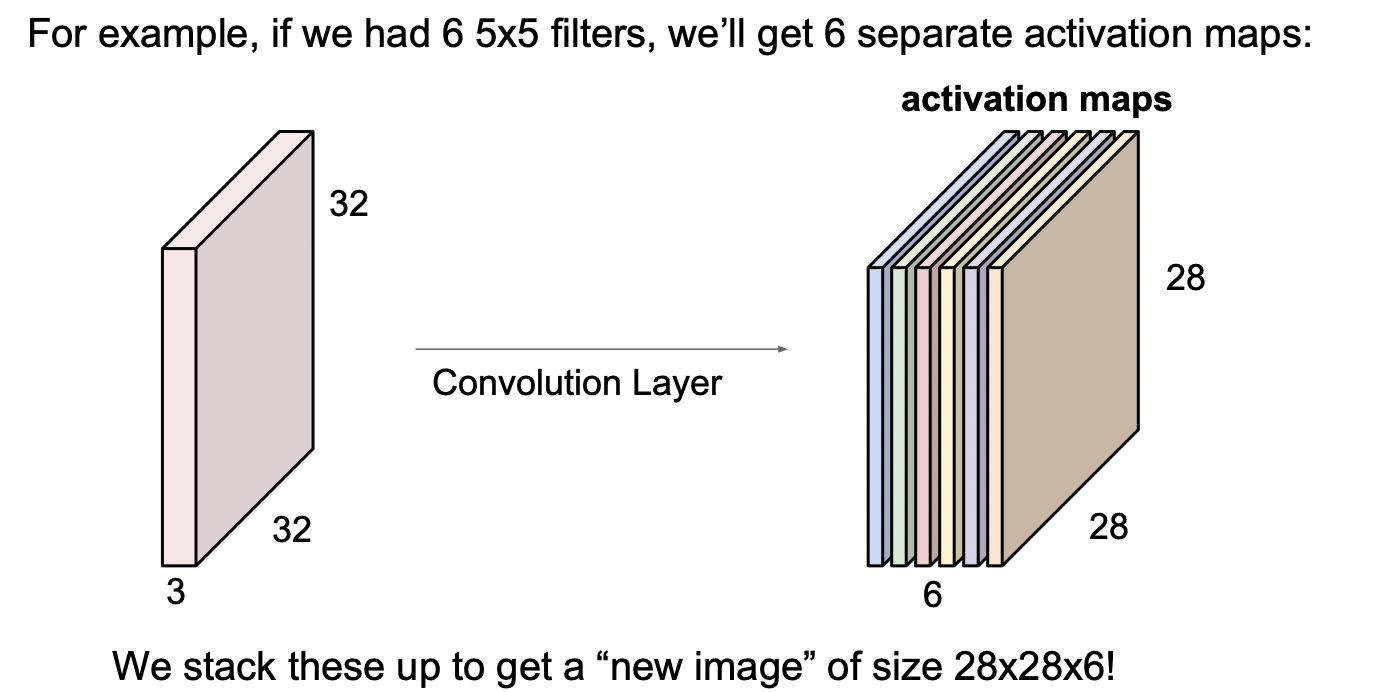
예시로 5x5필터 6개, 여러가지 특징을 가진 필터들을 가지고 연산을 수행했을 때 activation maps이라는 출력값을 가지게 된다.

여러 개의 Layer들을 쌓고 나면 필터들이 계층적으로 학습을 하는 것을 볼 수있다. 위의 그림에서 빨간색 박스를 보면 Edge와 같은 low-level feature이 보이지만, 파란 박스를 보면 형태와 같은 high-level feature을 볼 수 있다.
전에 했던 예시를 보면, 32x32x3인 이미지가 Convolution 연산을 하게 되면 28x28x6으로 이미지의 사이즈가 줄어든 다는 것을 알 수 있다.
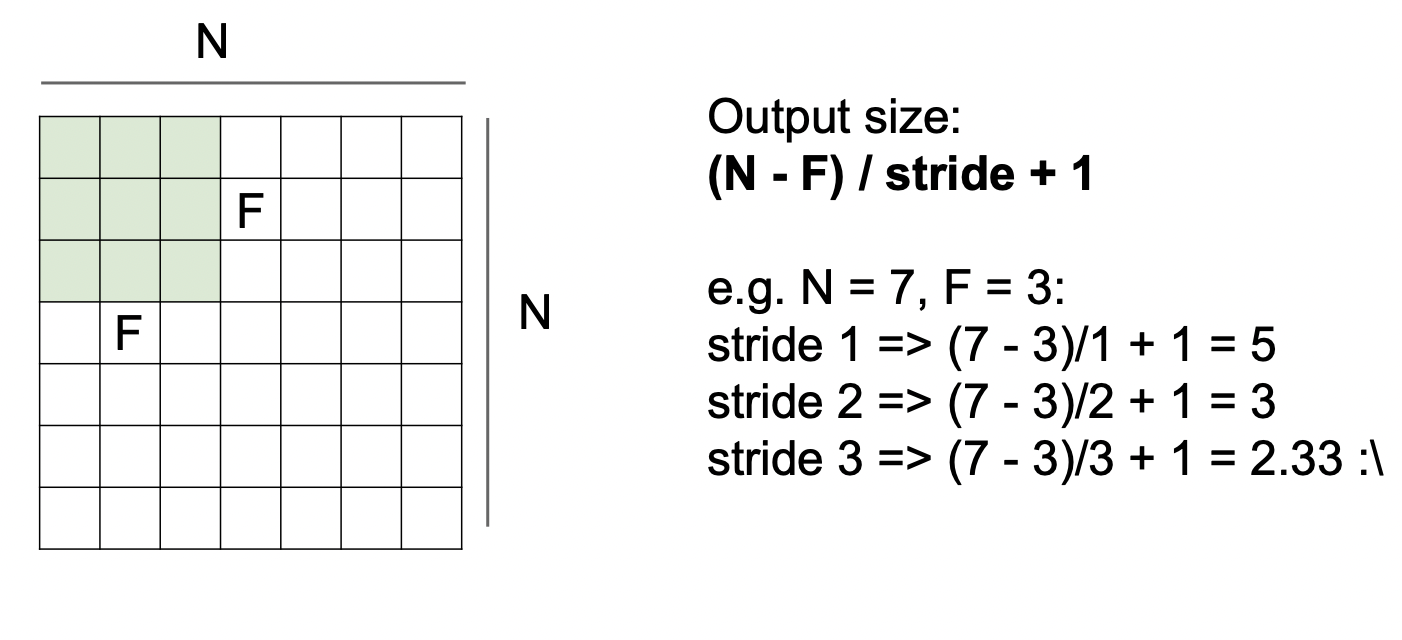
Output size는 (N-F)/stride +1의 공식을 가지면, 여기에서 stride는 보폭으로 필터가 한번에 움직이는 크기를 말하고, N은 인풋 이미지의 크기, F는 필터의 크기를 말한다.
위의 예시에서 stride 3을 하면 소숫점이 나오므로 만약에 stride를 3으로 하게 되면 이상한 값이 나온다.

인풋 이미지와 아웃풋 이미지의 크기를 같게 해주는 방법 중에 하나가 zero padding이다. 말그대로 모서리에 0의 값을 추가하는 방식인데 이를 이용하면 이미지 크기가 같게 나올 뿐 아니라 필터의 중앙이 닿지 않는 모서리에 있는 값들을 계산할 수 있게 된다.
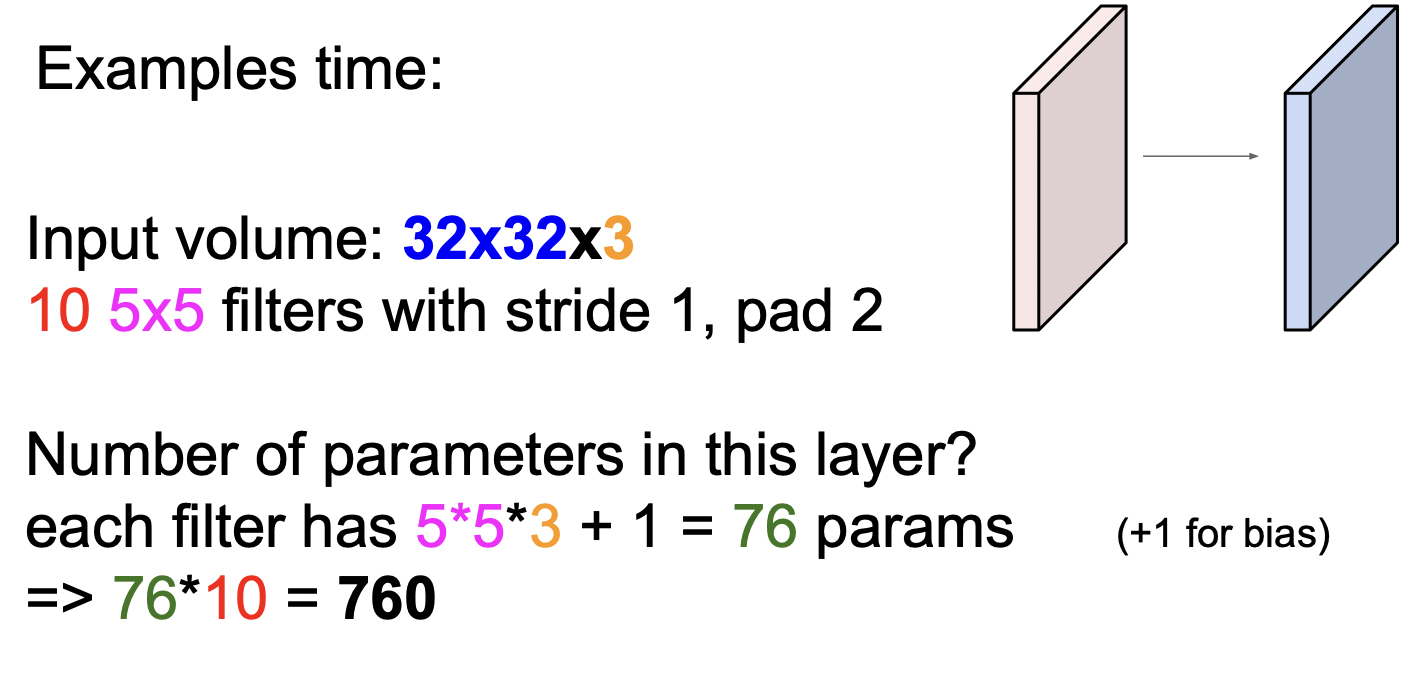
이미지의 크기가 32x32x3이고, 크기가 5x5x3이며, stride 1, pad 2, 10개인 필터가 있다고 할 때, 파라미터가 몇 개 일까.
먼저 필터의 사이즈에 편향(bias)를 더한 값인 5x5x3+1 = 76에 필터의 갯수인 10을 곱하면 760이 나온다.
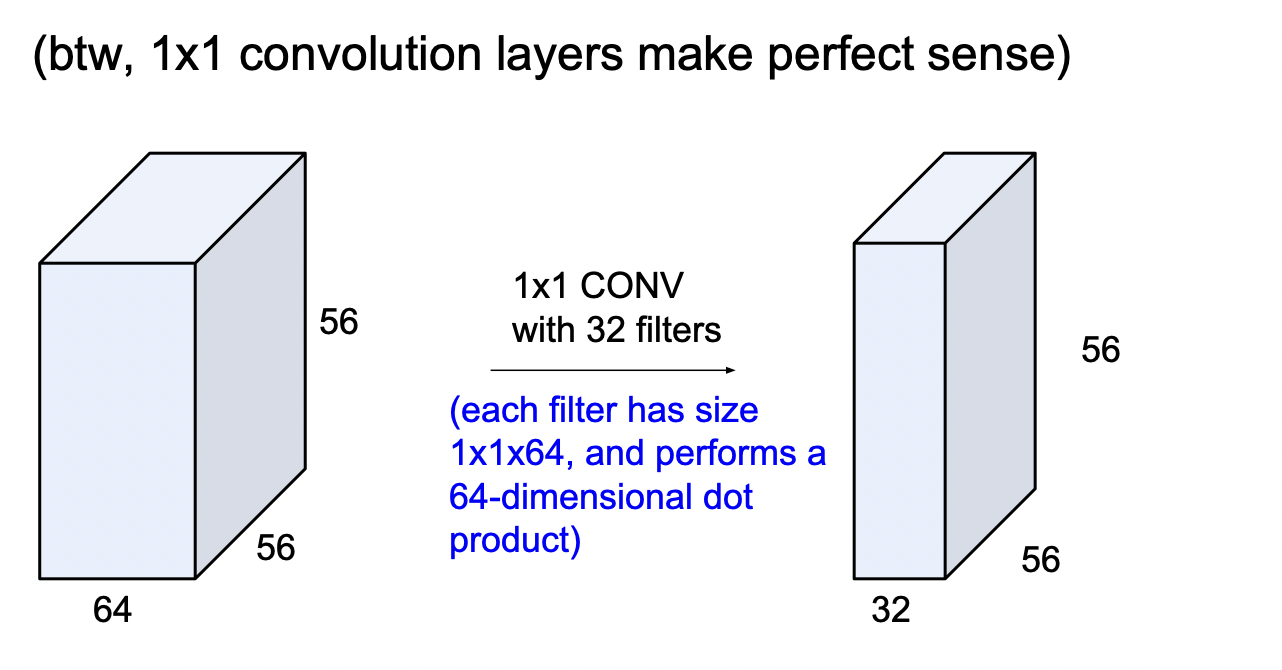
참고로, 1x1의 크기를 가진 필터 32개로 연산을 수행하게 되면, 56x56x64에서 56x56x32가 된다. 패딩을 하지 않아도 이미지의 크기는 유지되며 깊이만 필터의 갯수에 맞게 변한다.
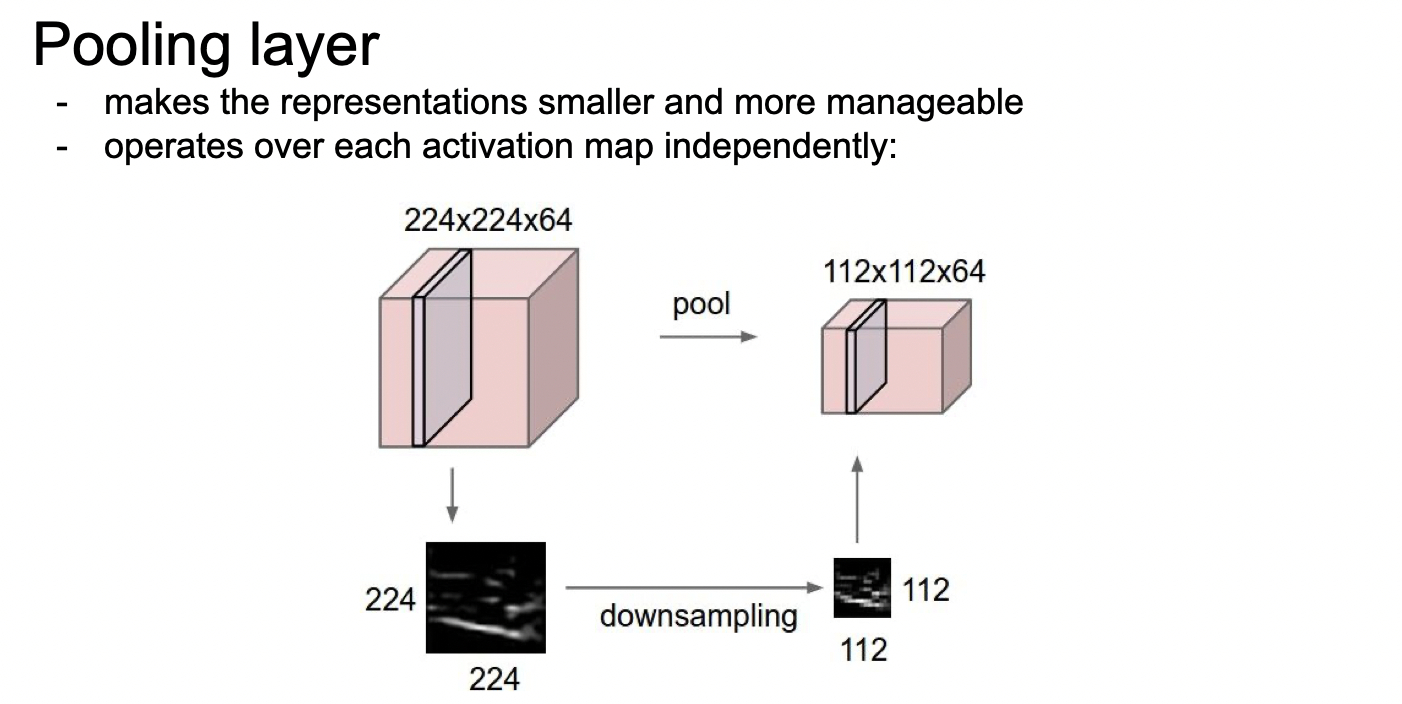
Pooling layer은 파라미터의 수를 줄이면서, 동시에 일종의 공간적인 불변성을 얻는다.
한 마디로 공간이 가지는 특성은 유지한채 파라미터의 수만 줄인다. Downsampling하는 방법 중에 하나이다.
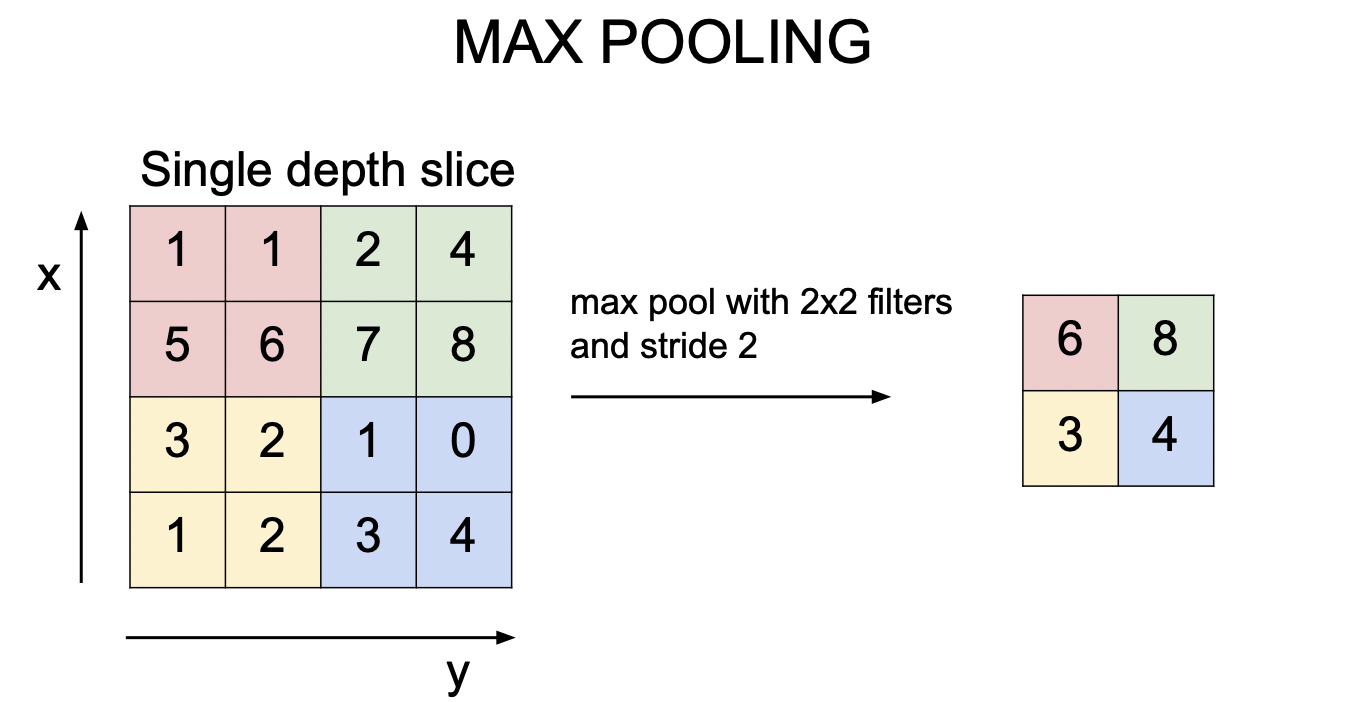
맥스 풀링은 지역에서 가장 큰 값을 출력하는 연산이다. 따라서 가장 큰 값을 계산 하는 것이므로 따로 파라미터는 없다.

요약
- ConvNets은 CONV, POOL, FC레이어들을 쌓는다.
- 작은 필터들을 이용해 더 깊은 구조를 가지는 방향으로 트렌드가 있다.
- 전형적인 구조는 다음과 같다.
[(CONV-RELU)*N-POOL?]M-(FC-RELU)K, SOFTMAX
N은 ~5까지, M은 크고, 0<=K<=2. - 하지만 요즘은 ResNet/GoogLeNet 같은 것들은 이런 패러다임에 도전한다.
키워드 : Fully Connected Layer, Convolution Layer, activation map, 필터, zero-padding, Pooling Layer, Max Pooling
