오늘은 자료구조 한파트 끝내고, C언어 한파트 복습하고, 백준 문제 풀어야겠다.
자료구조 공부를 하다보니, C언어 복습 내용 안한거 조금이 계속 발목을 잡아서 한번 익힌걸 머리에 박아넣질 못하고있다. 빨리빨리 해야지.
2장, 재귀 (Recursion)
재귀에 대해서는 그동안 문제 풀 때나 수학 공부를 하며 많이들 들었다. 당연히 어느정도는 익숙한 내용이지만, 기본적인 개념을 확실하게 잡는게 심화학습을 할 수 있게 해주는 데에 첫 발걸음이기 때문에 개념부터 다시 잡겠다.
02-1
우선, 재귀함수란?
"함수 내에서 자기 자신을 다시 호출하는 함수"
void Recursive(void) {
printf("Recursive Call\n");
Recursive();
}만약 위의 example 코드처럼 코드가 진행이 된다면, 끊임없이 Recursive Call이 출력 될 것이다. 보통 우리가 이해하는 재귀는
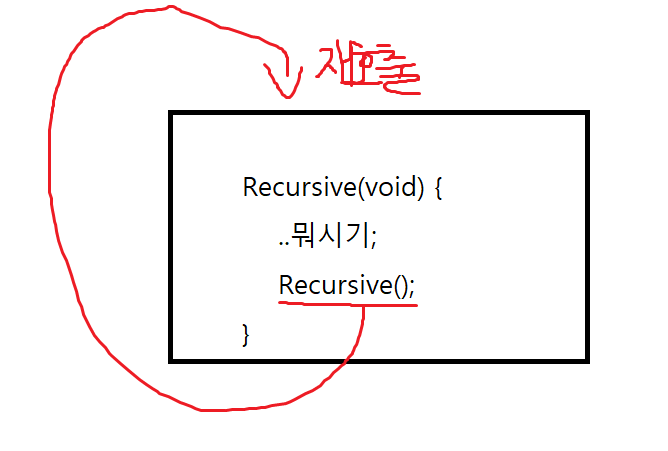
위와 같은 그림처럼 이해할 것이다.
이 책의 저자는 이 그림도 맞다곤 하지만, 재귀함수의 흐름을 쉽게 파악하기 위해 다음 그림과 같이 이해하라고 한다.
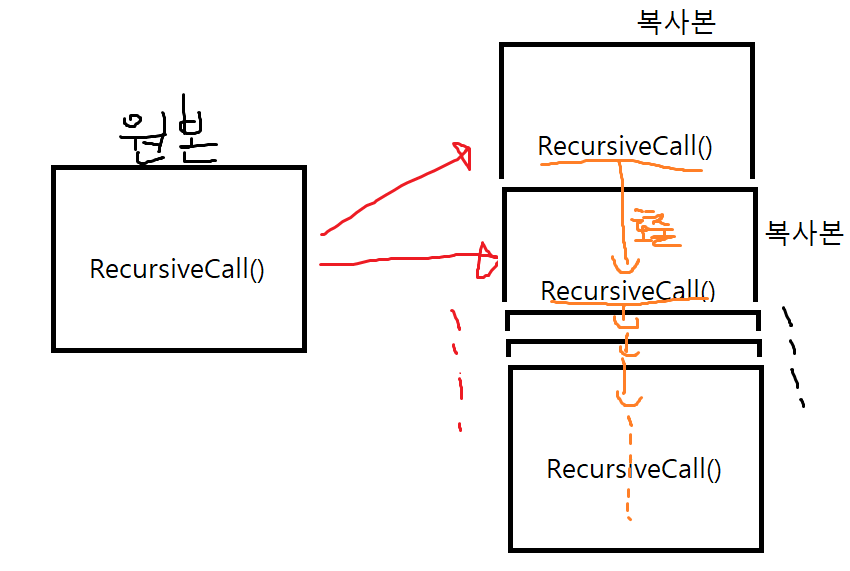
요렇게.
Recursive가 호출되면 Recursive의 복사분이 만들어져서 실행, 이 과정이 반복...
이렇게 이해하자.
그러면 이 재귀함수의 예시론 뭐가있냐?
n! = n x (n-1) x (n-2) x (n-3) .. x 2 x 1
음..
보면 계속 같은 패턴이 반복되고 있다.
n 에 n에서 1이 빠진 (n-1)이 곱해지고, (n-1)에서 1이 빠진 (n-2)가 곱해지고.
int factorial(int n) {
if (n == 0) return 1;
else return n * factorinal(n-1);
}이렇게 하면, 방금 내가 말한 "반복되는 패턴"이 함수 내에서 구현되고 있지 않은가. 이렇게, 재귀함수에 대한 이해도를 한층 높였다.
02-2
그러면 이 재귀를 어디에 활용되는지, 팩토리얼을 말고도 다른 사례들을 코드로 구현해나가면서 재귀를 체화시켜보자.
- Fibonacci Sequence
피보나치 수열.
0, 1, 1, 2, 3, 5, 8 , 13..
앞의 두 수를 더하여 현재의 수를 만들어 나가는 수열이다.
이 피보나치수의 n번째 수를 구한다 가정했을 때,
n이 1일땐 0, n이 2일땐 1, 이후의 n은 (n-1)번째 수 + (n-2)번째 수.
int fibo (int n) {
if (n==1) return 0;
else if (n==2) return 1;
else return fibo(n-1) + fibo(n-2);
}
이렇게 구현하면 되지 않겠는가. Good.
그리고 앞서 공부했던 Binary Search Algorithm도 한번 재귀를 사용해서 공부해보자.
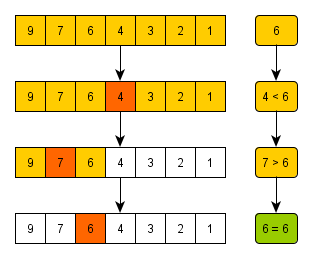
저번 Ch.01을 복습할 때 썼던 그림이다.
mid값과 target값의 대소 구분 후 반 자르고. 다시 mid값 설정.
mid값과 target값의 대소 구분 후 반 자르고. 다시 mid값 설정.
mid값과 target값의 대소 구분 후 반 자르고. 다시 mid값 설정.....
똑같은 과정의 반복이다.
그러면 이걸 일반화 시키면
- 탐색 범위의 중앙(mid)에 목표 값이 저장되어있는지 확인.
- If 저장되어있지 않다면, 탐색범위를 반으로 줄여서 다시 탐색.
이렇게 할 수 있다.
그러면 여기에 필요한 자료들은
- target
- target을 탐색할 배열
- 배열의 처음부분
- 배열의 마지막 부분
이렇게 자료들이 필요할거다. 이걸 사용해서 함수를 구성하면
BSearchRecur(int arr[], int target, int first, int last)이렇게 함수 원형을 설정해줄 수 있다.
그러면 여기서 앞서 일반화 시킨 순서의 첫번째.
"탐색 범위의 중앙에 목표값이 저장되어 있는가"
..의 이전에, 이 탐색이 실패했을 때를 먼저 반환해보자.
이진 탐색 알고리즘에서, first값이 last값보다 커지게 되면 "탐색 실패"로 반환하게된다.
BSearchRecur(int arr[], int target, int first, int last) {
if (first > last) return -1; //-1이 실패를 뜻함
}그 다음, "탐색 범위의 중앙에 목표값이 저장되어 있는가"
BSearchRecur(int arr[], int target, int first, int last) {
int mid; // 중앙값
if (first > last) return -1; //-1이 실패를 뜻함
mid = (first + last) / 2;
if (arr[mid] == target) return mid;
}이후, If 저장되어있지 않다면, 탐색범위를 반으로 줄여서 다시 탐색.
BSearchRecur(int arr[], int target, int first, int last) {
int mid; // 중앙값
if (first > last) return -1; //-1이 실패를 뜻함
mid = (first + last) / 2;
if (arr[mid] == target) return mid;
else if (target < arr[mid]) {
BSearchRecur(arr, target, first, mid - 1);
} else {
BSearchRecur(arr, target, mid + 1, last);
}
}이렇게, 구현할 수 있다.
02-3
앞서 팩토리얼과 피보나치 수열을 학습했다면, 이번엔 하노이 타워다.
하노이 타워가 뭔지는 아마 다들 보면 알거다. 이름을 모를 순 있지만, 이 대상을 모를 순 없달까.

욜케 생긴거.
왼쪽에 가득 쌓인 탑을 맨 오른쪽에 있는 짝대기로 고대~로 옮기는 문제.
뭐 어떻게 푸는진 아니까, 반복 패턴만 찾아보겠다.
원반 n개와 A / B / C 작대기가 있다고 가정하겠다. 원반 n개는 A 작대기에 있다.
원반 전체를 C로 옮기려면, (n-1)개의 원반들을 B로 먼저 옮겨야한다.
그 다음, A에 있는 가장 큰 원반을 C로 옮긴다.
그 다음, B에 있는 (n-1)개의 워반들을 C로 옮긴다.
?? 지금 이걸 읽으면서 패턴이 있다는걸 어느정도 못 느꼈는가?
- 작은 원반 (n-1)개를 B로 이동
- 가장 큰 원반 1개를 C로 이동
- B에 있는 (n-1)개의 작은 원반을 C로 이동
이렇게 하면 된다!
그러면, 함수를 만들어 보겠다.
int HanoiTower(int n, char from, char by, char to) {
}이렇게 함수 원형을 구성한다.
그리고 만약 원반이 1개가 남는다면, 그냥 옮기면 끝일거다.
int HanoiTower(int n, char from, char by, char to) {
if (n==1) printf("원반을 %c에서 %c로\n", from, to);
}이제 순서대로 나가보자.
- 작은 원반 (n-1)개를 B로 이동
int HanoiTower(int n, char from, char by, char to) {
//from에서 by를 거쳐 to로 이동이라고 생각하자
if (n==1) printf("원반을 %c에서 %c로\n", from, to);
else {
HanoiTower(n-1, from, to, by); //a에서 c를 거쳐 b로 이동
}
}- 가장 큰 원반 1개를 C로 이동
int HanoiTower(int n, char from, char by, char to) {
//from에서 by를 거쳐 to로 이동이라고 생각하자
if (n==1) printf("원반을 %c에서 %c로\n", from, to);
else {
HanoiTower(n-1, from, to, by);//a에서 c를 거쳐 b로 이동
printf("가장 큰 원반을 %c에서 %c로\n", from, to);
// 가장 큰 원반을 C로 이동
}
}- B에 있는 (n-1)개의 원반을 C로 이동
int HanoiTower(int n, char from, char by, char to) {
//from에서 by를 거쳐 to로 이동이라고 생각하자
if (n==1) printf("원반을 %c에서 %c로\n", from, to);
else {
HanoiTower(n-1, from, to, by); //a에서 c를 거쳐 b로 이동
printf("가장 큰 원반을 %c에서 %c로\n", from, to);
// 가장 큰 원반을 c로 이동
HanoiTower(n-1, by, from, to); //b에서 a를 거쳐 c로 이동
}
}쨔쟌-! 해결했땅. ㅎㅎ~
몇 줄도 안되는 코드로 하노이의 탑을 코드로 구현했다. 이래서 재귀를 쓴는게 아닐가..?
나중에 백준으로 여러 문제들 구현해나가며 재귀를 더욱 체화시켜보자.
여기까지.