Ch.08 Tree
Tree. 앞서 단순하게 데이터를 저장하게 뽑아내기만 했던 뭐 List, Stack, Queue, Deque.. 과는 전혀 다르다. 방금 말한 이런 자료구조들은 선형 자료구조이지만, 이번에 학습할 트리는 비선형 자료구조이기때문에 집중해서 공부를 해야한다.
우선, 트리란 무엇이냐.
계층적 관계를 표현하는 자료구조
를 말한다.
그리고 여기서 초점을 둬야할게, 계층적 관계? 뭐 당연히 중요한 말이지만, "표현"하는 자료구조. 라는 말도 중요하다.
앞서 우리가 자료구조랍시고 배운 애들은 다 "뭔가 저장하고 꺼내는거!" 라는 느낌으로 익혔는데, 자료구조 라는 것이 근본적으로 무엇인가를 "표현하는" 도구 라는 것을 잊으면 안된다.
이후 트리의 ADT를 정의할 때, "이건 이렇게 데이터를 저장하는구나~" 라는 느낌보단, "트리의 구조로 이루어져있는 무엇인가를 구현하려고 할때, 이를 표현하기에 적절히 정의되어있는가?" 라고 생각하는게 맞다.
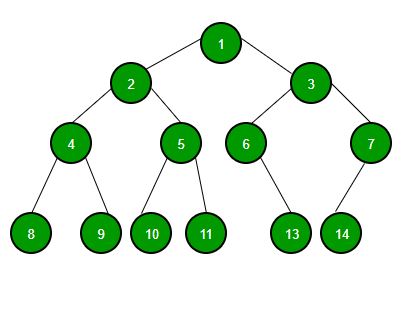
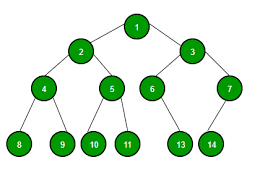
위와 같은 구조의 구조를 "Tree"라고 한다. 왜냐고? 나무가 가지를 뻗으면서 점점 넓어진다는 특성을 생각해서 Tree라고 한단다. 집안 족보 / 정부 조직도 같은 경우를 생각하면 된다.
그러니까 아까 말했듯, 앞서 선형 자료구조에서 배운 것처럼 "이 자료구조에서 어떻게 데이터를 Push하고 Pop해야해" 라는 생각 말고, "이 Tree 구조로 어떤 걸 표현할 수 있겠네" 라고 생각해야하는게 맞다는거다. 자료구조는 "표현하는" 도구니까. 앞서 선형의 Stack을 예로들면 얘는 "데이터를 저장하는걸 Stack으로써 표현한것"이라는거다.
그 다음으론 트리 관련 용어들이다.
직접 그린 그림 하나에 설명을 곁들여보겠다.
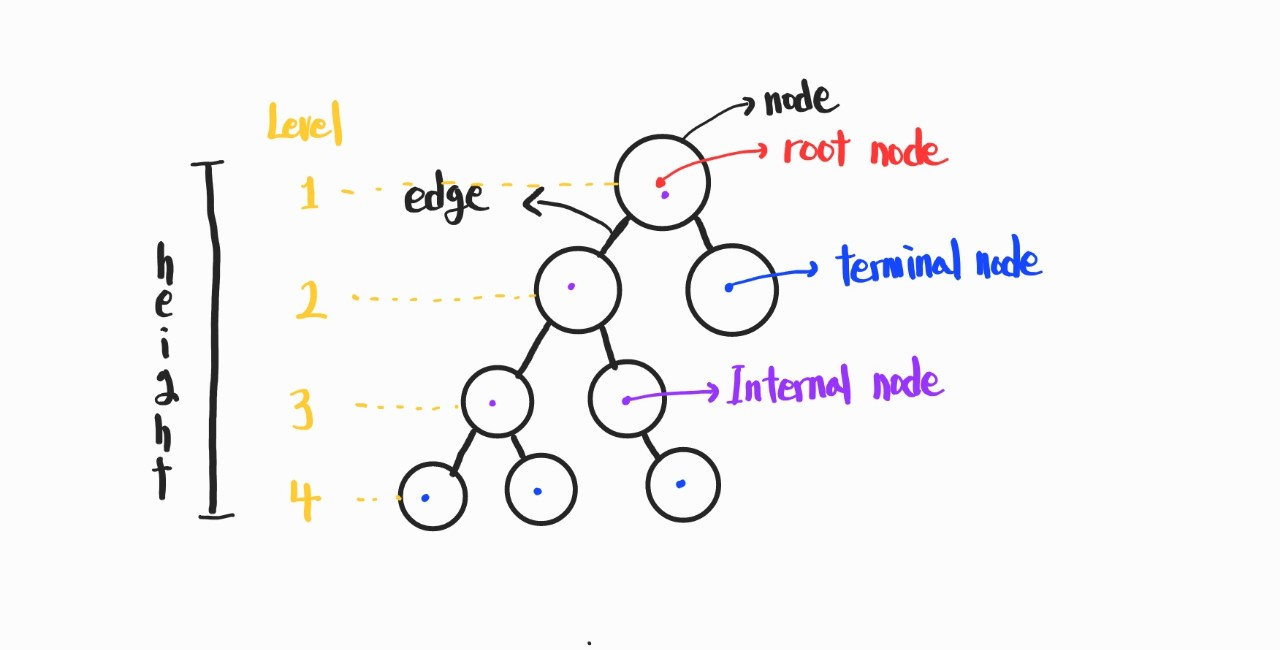
사진이 좀 작을수도 있으나.. 확대해서 보든가 하자.
node(노드) : 트리의 구성요소. 동그라미가 싹 다 노드.
edge(간선) : 노드와 노드를 연결하는 선 전부 다.
root node(루트 노드) : 트리 구조 최상위의 노드 하나. 시조라고 생각하자.
terminal node(단말 노드, 잎사귀 노드) : 아래에 또 다른 노드가 연결되어있지 않은 노드. 파란 점에 해당한다.
internal node(내부 노드, 비단말 노드) : 단말노드 빼고 전부 다.
height(높이) : 해당 Tree의 높이.
level(레벨) : 해당 Tree의 각 층을 level이라고 함.
그리고, 각 노드 간에는 부모 / 자식 / 형제 관계가 성립이 된다. 그냥 그림 보면 알거다. 3층에 있는애들끼리는 형제. 3층 입장에선 2층은 부모. 3층 입장에서 4층은 자식. 이렇게.
이렇게 간단한 트리의 구성 요소에 대한 설명은 끝냈고. 이제 "트리" 자체에 대한 용어다.
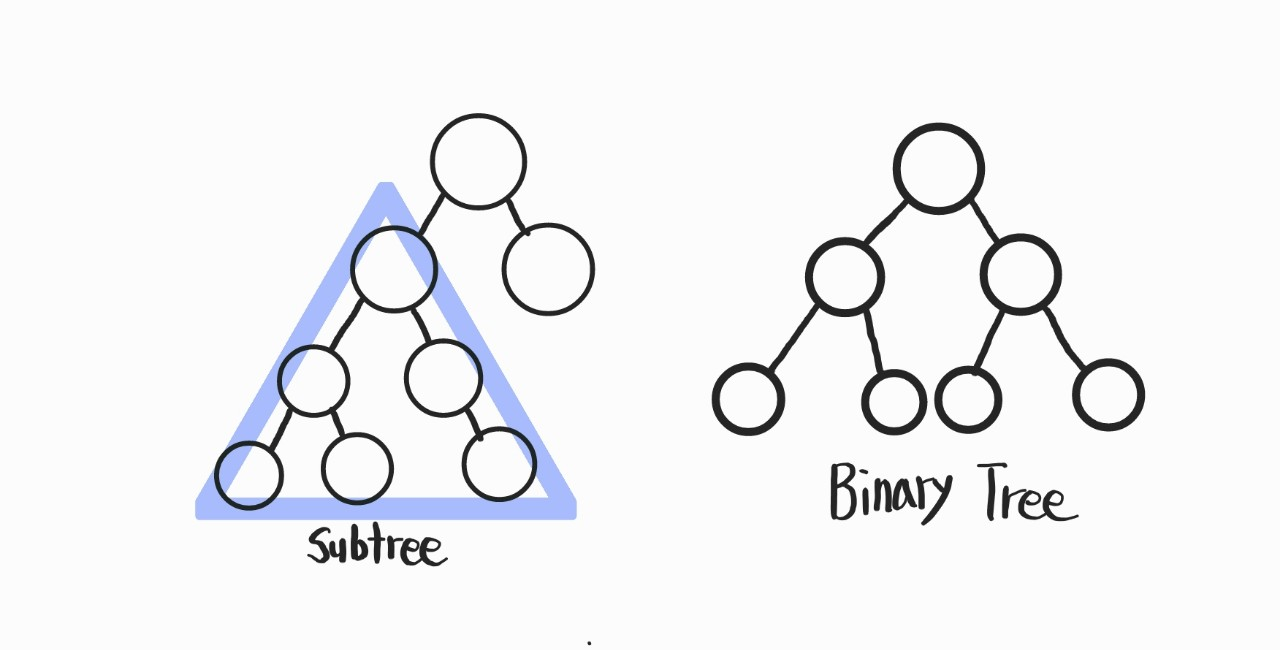
왼쪽처럼 큰 트리 안에 속해있는 작은 트리는 Sub Tree(서브 트리) 라고 한다.
오른쪽의 경우에는 트리 중 특이케이스로 Binary Tree(이진 트리) 라고 하는데, 이게 이진 트리가 되려면 두 조건을 만족해야 한다.
- 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어진다.
- 나뉘어진 두 서브 트리도 모두 이진트리여야 한다.
이 두 조건인데, 또 이 이진 트리의 특징이 하나가 더 있다.
바로..
- 노드가 위치할 수 있는 곳에 노드가 존재하지 않는다면, Empty Set(공집합) 노드가 존재하는 것으로 간주한다.
이게 무슨소리냐면,
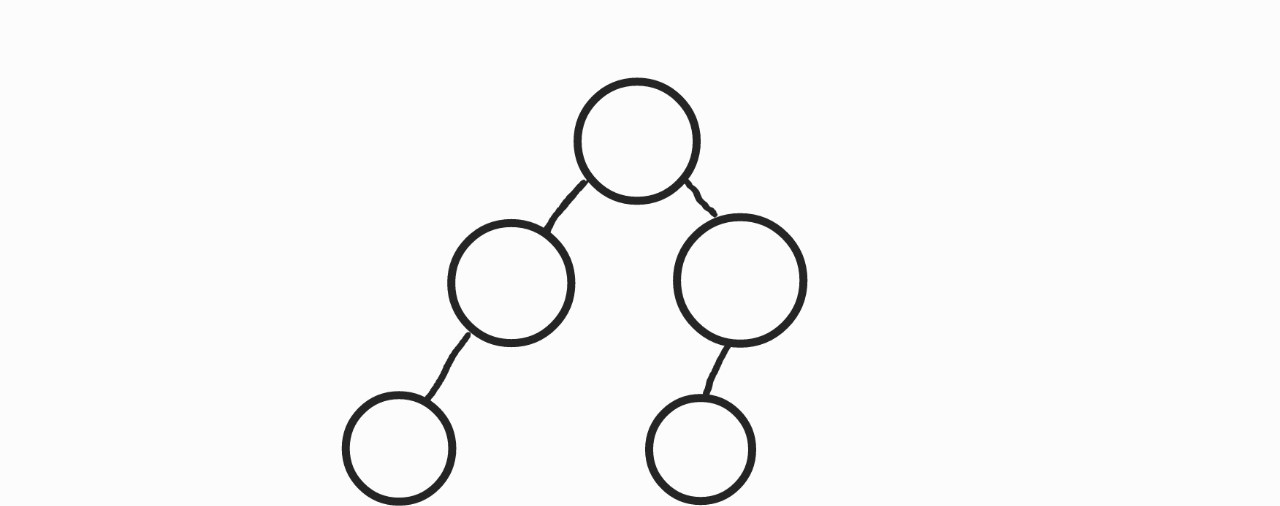
만약 이런 트리가 있다면, 이건 그냥 별 특징 없는 일반적인 트리일까?
.. 아니다.. 이진 트리가 되기 위한 위에서 언급한 1, 2, 3번 조건을 모두 만족시키므로, 이진 트리가 된다.
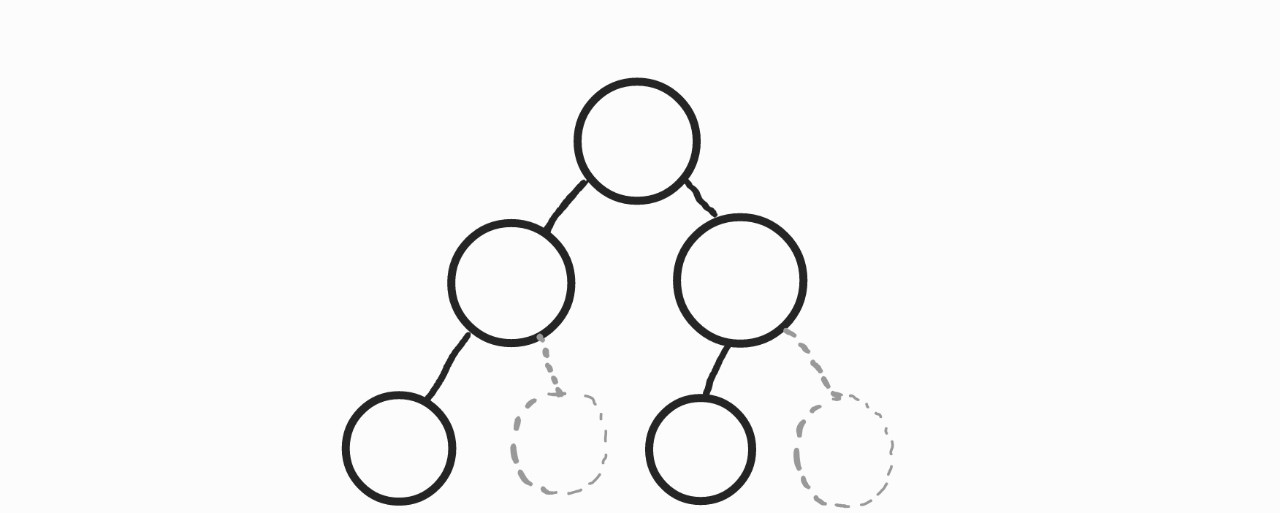
이렇게 공집합노드(점선 부분이 공집합 노드)가 존재한다고 인정되므로, 이진 트리가 되는 것이다.
그리고 위의 예시 (SubTree 예시 그림 옆에 있는 트리) 공집합 없이 모든 레벨이 꽉 찬 트리를 포화 이진 트리라고 하고,
레벨이 꽉 차있진 않지만 빈 틈(공집합) 없이 노드가 채워진 이진 트리를 완전 이진 트리라고 한다.
오늘은 여기까지.
내일은 구현을 복습해보겠다.