인간의 욕심은 끝이 없고 같은 실수를 반복한다.
나는 잠과 나태함을 이겨내지 못하는가보다.. 끝 없는 반성과 다시 실수의 반복. 후우.....
Ch. 08-2, 이진 트리 구현
08-2
앞서 공부했던 트리를 구현한다.
일단, 이 이진 트리도 앞서 List들처럼 배열 기반으로도 만들 수 있고, 연결 리스트 기반으로도 만들 수 있다.
그리고, 이번에 Tree를 만들 때 고려해야할 Key Point는,
노드에 고유의 노드 번호가 부여되어 있다는 점이다. 이 고유의 노드 번호는, 데이터가 저장되어야 할 배열의 인덱스 값을 의미한다고 생각하자.
그러면 일단, ADT를 정의한 헤더 파일을 한번 보자.
일단은 연결리스트 기반의 Tree이다.
/* BTree.h */
#ifndef __B_TREE_H__
#define __B_TREE_H__
typedef int BTData;
typedef struct _bTreeNode {
BTData data;
struct _bTreeNode *left;
struct _bTreeNode *right;
} BTreeNode; // Tree의 Node를 의미하는 구조체다.
BTreeNode *MakeBTreeNode(void); // 노드 만들기
BTData GetData(BTreeNode *bt); // 노드에 저장된 데이터 가져옴
void SetData(BTreeNode *bt, BTData data); // 노드에 데이터 저장
BTreeNode *GetLeftSubTree(BTreeNode *bt);
BTreeNode *GetRightSubTree(BTreeNode *bt);
// 각 각 왼쪽, 오른쪽 SubTree의 주소값을 가져온다.
void MakeLeftSubTree(BTreeNode *main, BTreeNode *sub);
void MakeRightSubTree(BTreeNode *main, BTreeNode *sub);
// 인자 sub로 전달된 서브트리or노드를
// main으로 전달된 노드의 각각 왼쪽, 오른쪽으로 연결한다.
#endif뭐 크게 특별한 기능은 없다.
노드의 구조체가 존재한다는 점.
그리고 ADT로 정의된 각 함수들의 역할. 정도?
그리고 조금 다른걸 알아둬야 한다면, MakeBTreeNode로 만들어진 노드 하나는 공집합 노드 두개를 왼쪽 하나, 오른쪽 하나로 가지고 있는 이진트리로 생각해도 된다는 점이다.
그리고, MakeBTreeNode 는 앞에 *로 주소값을 반환해준다는것도 알아두면 된다. 비어져있는 노드 하나의 주소값을 어떤 변수에 저장해놓고, SetData와 MakeLeftSubTree, MakeRightSubTree를 사용할 때 이 주소값을 사용해서 Tree를 만들어준다.
BTreeNode *bt = MakeBTreeNode();
BTreeNode *btb = MakeBTreeNode();
SetData(bt, 1);
SetData(btb,2);
MakeLeftSubTree(bt, btb);이렇게.
그러면 이제 위의 헤더파일을 소스파일로 구현해보자.
아마 정~말 별 거 없어서, 딱히 주석으로 설명할 것 조차 없을거다..
/* BTree.c */
#include <stdio.h>
#include <stdlib.h>
#include "BTree.h"
BTreeNode *MakeBTreeNode(void) {
BTreeNode *new = (BTreeNode *)malloc(sizeof(BTreeNode));
new->left = NULL;
new->right = NULL;
return new;
}
BTData GetData(BTreeNode *bt) {
return bt->data;
}
void SetData(BTreeNode *bt, BTData data) {
bt->data = data;
}
BTreeNode *GetLeftSubTree(BTreeNode *bt) {
return bt->left;
}
BTreeNode *GetRightSubTree(BTreeNode *bt) {
return bt->right;
}
void MakeLeftSubTree(BTreeNode *main, BTreeNode *sub) {
if (main->left == NULL) {
free(main->left);
} // 만약 main의 왼쪽에 이미 subtree가 있다면, 비워주고 다시 만든다
main->left = sub;
}
void MakeRightSubTree(BTreeNode *main, BTreeNode *sub) {
if (main->right == NULL) {
free(main->right);
} // 만약 main의 오른쪽에 이미 subtree가 있다면, 비워주고 다시 만든다
main->right = sub;
}이렇다. 아마 앞의 연결리스트들에 비하면 함수의 구현이 정~말 별 거 없다고 느껴질거다.
그런데, 여기서 간과한 점이 하나 있다.
바로 MakeLeftSubTree와 MakeRightSubTree. 물론, 왼쪽이나 오른쪽에 만약 SubTree가 이미 존재한다면 비워주고 다시 새로 넣는게 맞다.
그런데, 지워야할 해당 SubTree의 아래에 다른 트리, 노드들이 이어져 있다면? 아마 그 노드, 트리들을 지울 방법은 사라지고, 메모리 누수가 일어나게 될 것이다. 이러한 실수를 범하지 않기 위해, "순회"라는 과정이 필요하다.
08-3
순회 (Traversal)
이 순회는 재귀적이다. 알아둬라.
이진 트리를 대상으로, 순회하는 방법은 총 세가지다.
- 전위 순회(Preorder Traversal) : 루트노드를 먼저
- 중위 순회(Inorder Traversal) : 루트노드를 중간에
- 후위 순회(Postorder Traversal) : 루트노드를 마지막에.
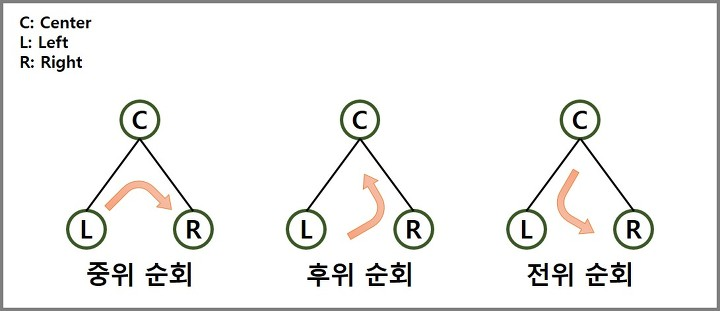
위와 같다.
아마 그림을 보면 무슨 말인지 대충 감이 올 것이기에, 굳이 따로 설명할 필요는 없을 것이다.
근데 만약, 우리가 순회할 트리의 높이가 2 이상이라면?
아까 말한걸 떠올리자, "순회의 과정은 재귀적이다".
중위 순회 과정으로 예시를 들어 보겠다.
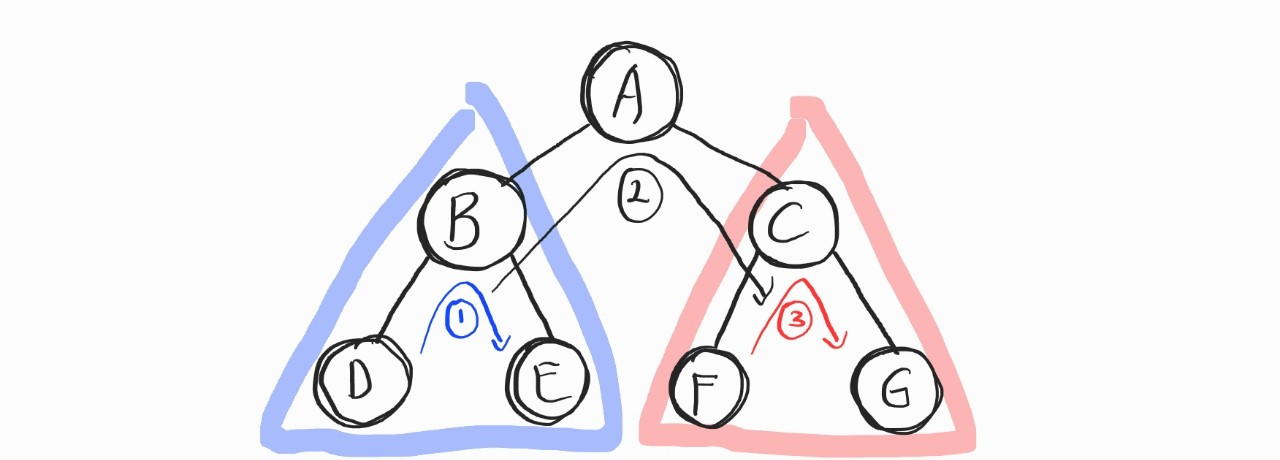
위의 그림을 참고한다면, 위의 그림에서 순회의 과정은
- 왼쪽 서브 트리 순회
- 루트노드 방문, 가장 큰 Main tree 순회
- 우측 서브 트리 순회
이다.
이걸 더욱 100% 이해하기 위해 코드로 설명을 해보겠다.
순회한다의 과정을 "해당 노드를출력 한다"를 기준으로 잡는다.
void Inorder(BTreeNode *bt) {
if (bt == NULL) { // 방문했는데 해당 bt NODE가 비워져있다면
return;
}
Inorder(bt->left);
printf("%d \n", bt->data);
Inorder(bt->right);
}이렇게 하면 된다.
전위 순회와 후위 순회? 그냥 중위 순회에서 뭐시기order 함수의 순서만 바꾸어주면 된다.
아니 근데 방문해서 출력하면 끝이에요? 내가 다른 기능 쓰고 싶을수도 있쟌아요
라고 불만을 제기할까봐, 노드를 방문해서 자유롭게 뭘 할지 구성할 수 있도록, 함수 포인터를 활용해서 응용해보겠다.
typedef void (*VisitFuncPtr) (BTData data);
void Inorder(BTreeNode *bt, VisitFuncPtr action);만약 BTree.h에 위와 같이 썼다고 치자.
PreOrderTraverse의 구체적인 구현은 바로 위에 있는거 참고.
그러면, 함수 포인터는 어떻게 써먹어야할까?
메인 함수를 한번 만들어보자. 여기서 써먹을거다.
#include <stdio.h>
#include "BTree.h"
void ShowIntData(int data) {
printf("%d \n", data);
}
int main() {
BTreeNode *bt1 = MakeBTreeNode();
BTreeNode *bt2 = MakeBTreeNode();
BTreeNode *bt3 = MakeBTreeNode();
BTreeNode *bt4 = MakeBTreeNode();
BTreeNode *bt5 = MakeBTreeNode();
BTreeNode *bt6 = MakeBTreeNode();
SetData(bt1,1);
SetData(bt2,2);
SetData(bt3,3);
SetData(bt4,4);
SetData(bt5,5);
SetData(bt6,6);
MakeLeftSubTree(bt1,bt2);
MakeRightSubTree(bt1,bt3);
MakeLeftSubTree(bt2,bt4);
MakeRightSubTree(bt2,bt5);
MakeRightSubTree(bt3,bt6);
Inorder(bt1,ShowIntData);
return 0;
}이렇게 main함수를 만들었다고 치자. 어떻게 출력될까?
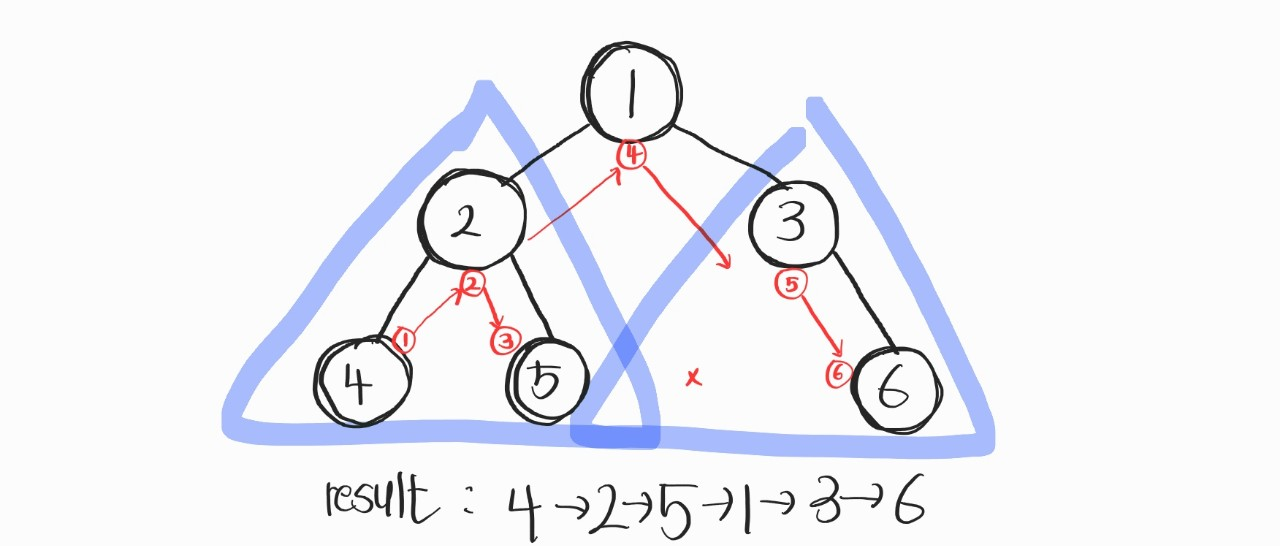
이렇게 출력 될 것이다. 노드의 방문 결과를 ShowIntData를 사용해서 "출력한다"를 기준으로 잡은 것이다. 물론 함수포인터를 응용해서 다른 목적을 구현해낼 수도 있다.
여기까지.