정렬에 대한 이야기를 이어서 해보자.
Sort
Quick Sort
퀵 정렬. 이름부터 Quick이라 뭔가 빨라보인다. 앞에 병합정렬이 꽤 어려웠어서 얘도 그만큼 어려울까봐 걱정할 수도 있는데, 다행히도 그정돈 아니다.
그래도, 기본 원리 자체는 막 쉬운건 아니긴 하다.
일단, 퀵 정렬의 기본 원리를 그림으로 보도록 하자.
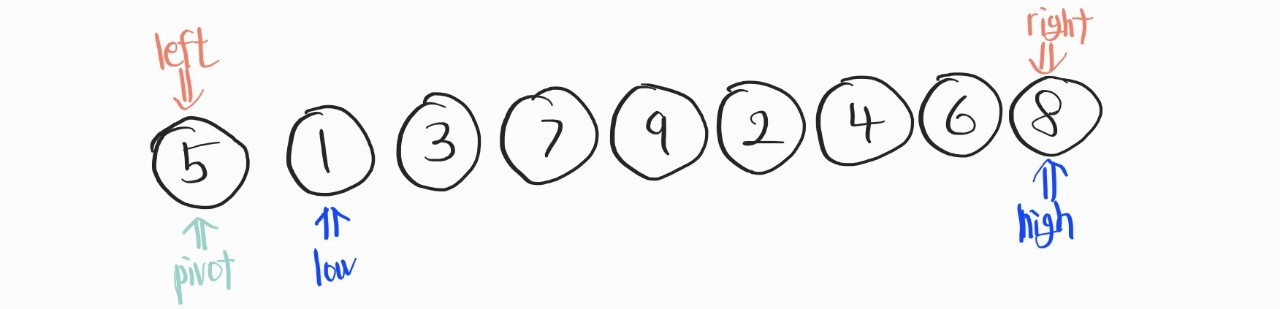
이렇게 정렬해야할 배열이 있으면, 위처럼 left, right, low, high, pivot 다섯개를 정한다.
여기서 정하는 기준은
-
left : 정렬 대상의 가장 왼쪽 지점
-
right : 정렬 대상의 가장 오른쪽 지점
-
low : 정렬 대상에서 pivot을 제외한 가장 왼쪽 지점
-
high : 정렬 대상에서 pivot을 제외한 가장 오른쪽 지점
-
pivot : 피벗. 정렬을 진행할 때 필요한 어떤 기준점.
여기서 위의 다섯개가 정해지면, 다음 과정을 거친다.
이 다음 과정은, low는 pivot보다 우선 순위가 낮은 요소를 만날때까지 우측으로 이동하고, high은 pivot보다 우선 순위가 높은 요소를 만날때까지 이동한다.
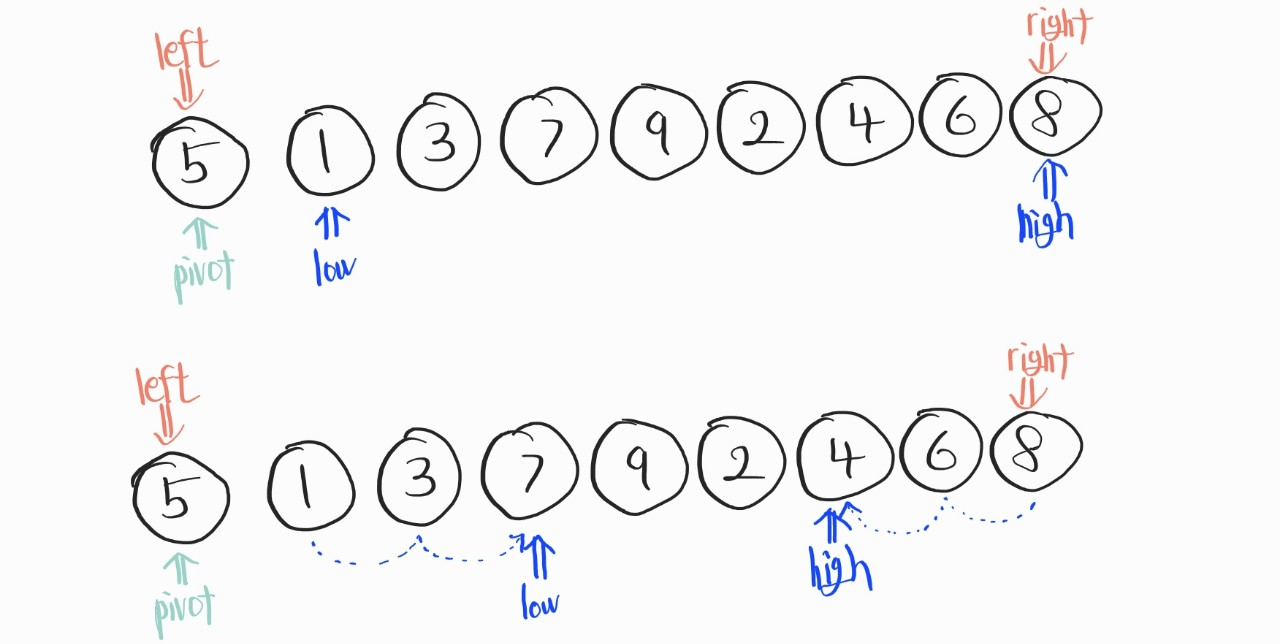
그리고, 이 low와 high지점에 있는 데이터를 변경해준다.
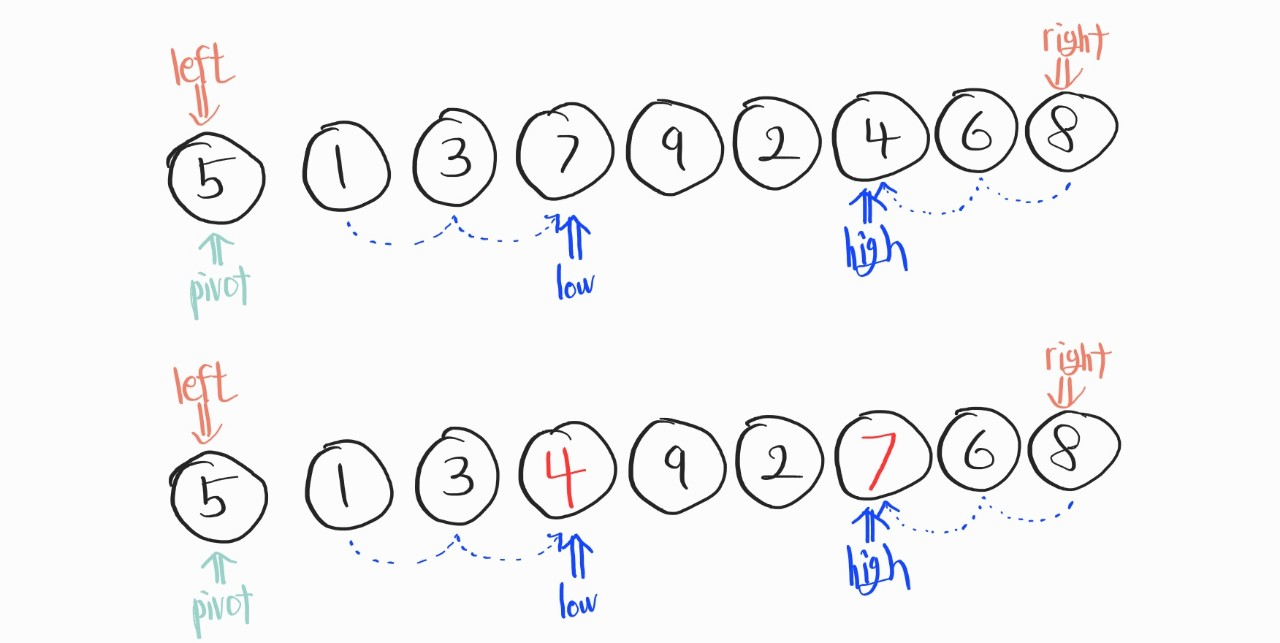
그 다음, 이어서 위의 과정을 다시 진행한다.
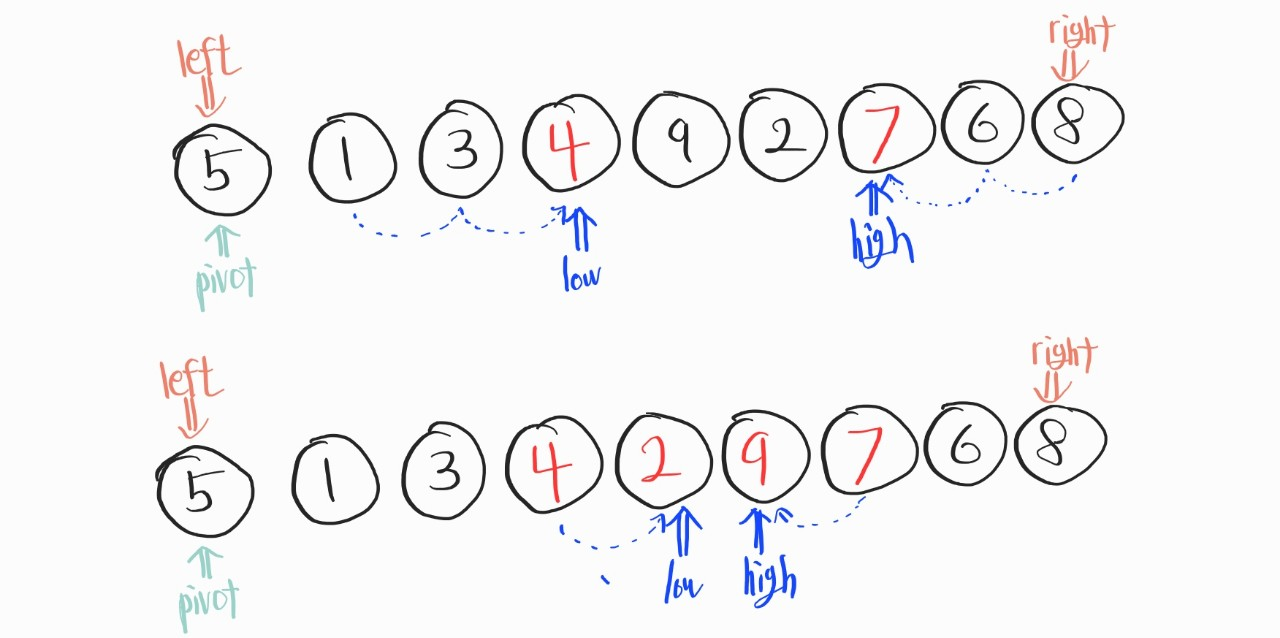
이렇게 진행하다 보면, 어느새 low와 high이 교차되는 상황이 일어날 것이다.
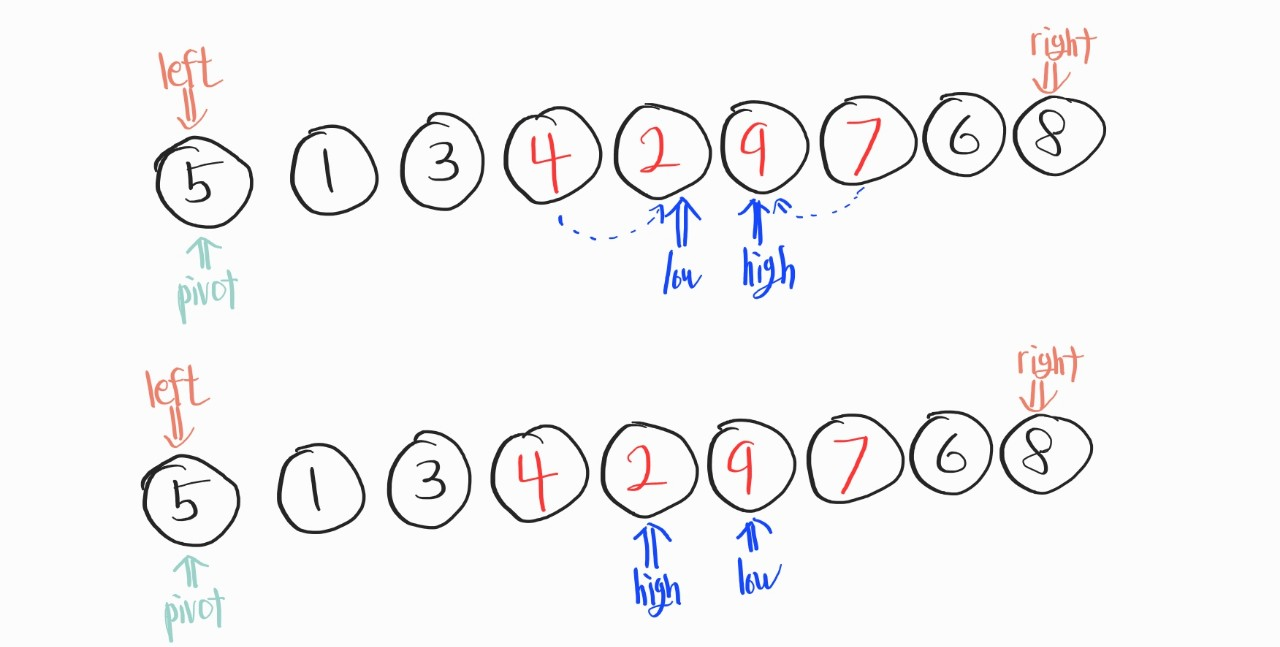
이런 상황이 오면, 이제 low와 high을 이용한 이동 및 교환과정이 완료되었음을 의미한다. 그래서 여기선 high과 pivot을 서로 교체해준다.
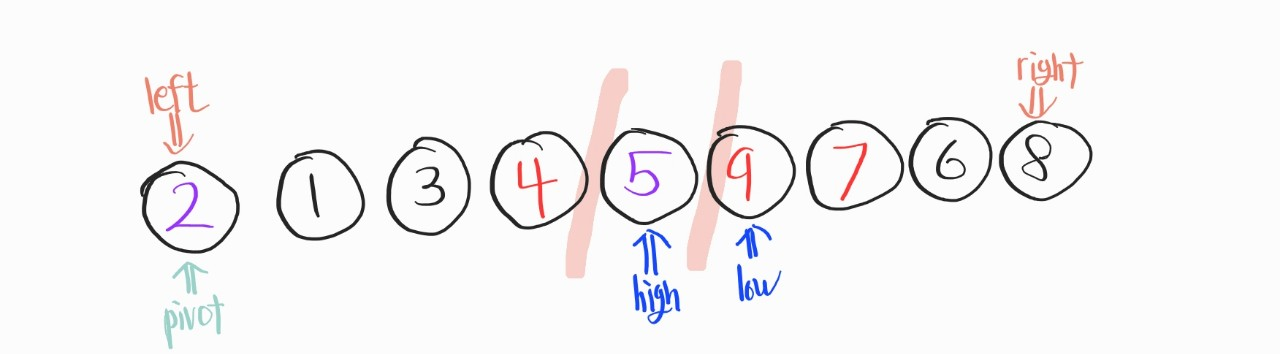
어? 이렇게 교체해보니..
기존의 pivot(5)을 기준으로 왼쪽은 기존의 pivot보다 우선순위가 높은 친구들이고, 기존 pivot을 기준으로 왼쪽은 기존의 pivot보다 우선순위가 낮은 친구들이다.
이렇게 된다면, 이 상태로 다시 5개의 기준을 정해줘서 QSort를 진행해준다.
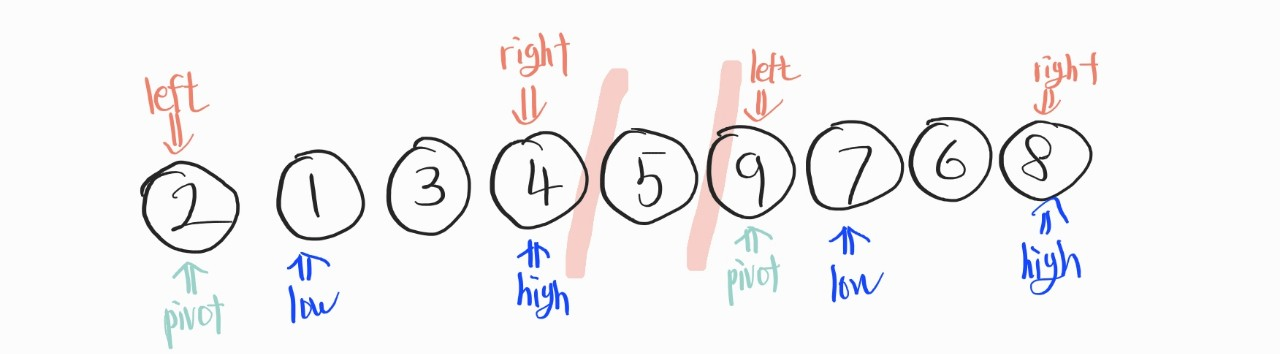
이 과정을, 이제 재귀적으로 반복해주면 된다.
이 반복은 left가 right보다 커지는 상황 (left > right)이 오게 된다면, 정렬이 끝나게 된다.
이를 구현해보자.
언제나 그랬듯, 자세한 설명은 주석에. 다음부턴 이 말도 굳이 안하겠다.
#include <stdio.h>
void Swap(int arr[], int idx1, int idx2) { // 그냥 Swap함수
int temp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = temp;
}
int Partition(int arr[], int left, int right) {
int pivot = arr[left]; // pivot은 가장 왼쪽의 data
int low = left+1; // low는 pivot을 제외한 가장 왼쪽의 data
int high = right; // high은 pivot을 제외한 가장 오른쪽의 data
while (high >= low) { // high과 low가 교차되기 전까진 반복
while (arr[low] <= pivot && low <= right) { // low의 데이터가 pivot보다 우선순위가 낮은 데이터를 만날 때 까지
low++; // low를 우측으로 하나씩 옮긴다
}
while (arr[high] >= pivot && high >= (left+1)) { // high의 데이터가 pivot보다 우선순위가 높은 데이터를 만날 때 까지.
// left + 1은 pivot을 제외시키기 위해.
high--; // high를 좌측으로 하나씩 옮긴다
}
if (low <= high) { // 만약 low와 high이 교차되지 않은 상태에서 위의 두 while문을 탈출하게된다면
Swap(arr, low, high); // low와 high을 서로 swap
}
}
Swap(arr, left, high); // pivot과 high이 가리키는 대상 교환
return high; // 옮겨진 pivot의 위치정보 반환
}
void QuickSort(int arr[], int left, int right) {
if (left <= right) {
int pivot = Partition(arr, left, right);
QuickSort(arr, left, pivot-1); // 재귀적 표현. pivot의 좌측 영역 정렬
QuickSort(arr, pivot+1, right); // 재귀적 표현. pivot의 우측 영역 정렬
}
}
int main() {
int arr[7] = {3, 2, 4, 1, 7, 6, 5};
int len = sizeof(arr) / sizeof(int);
int i;
QuickSort(arr, 0, len-1);
for (i=0 ; i<len ; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}그리고, 만약 더 좋은 성능을 기대해보고 싶다면, pivot을 처음 선정할 때 최대한 중간값을 선정해주는게 좋다.
이걸 대충 방법을 말로 설명해주면
"정렬 대상에서 임의로 세개의 데이터를 추출한 후, 그 중 중간값을 pivot으로 선택한다."
성능 평가
만약 pivot이 결정 되면, low와 high는 각각 이동을 시작한다. 그리고 그 이동은 이 두개가 서로 교차될 때까지 진행이되는데, 이동하는 과정에서 계속 피벗과의 비교를 수반한다.
while (arr[low] <= pivot && low <= right)
while (arr[high] >= pivot && high >= (left+1)
이렇게 두 문장을 보면, 위의 말이 맞다는 것을 알 수 있다.
그러므로, 하나의 pivot이 제자리를 찾아가는 과정에서 비교연산은 데이터의 개수인 n만큼 일어난다. pivot을 제외하고 n-1이지만, 빅-오를 따질때 -1 정도는 생략할 수 있으니까, 그냥 n이라고 하겠다.
그리고 맨 처음 비교를 1번 수행하면, 그 다음은 이 그림처럼

반으로 분할된 상태에서 다시 과정을 시작한다.
그러면 이 분할이 재귀적으로 게속 진행된다는 건데, 이 분할이 얼마나 일어나는지를 알아보자.
만약 데이터가 35개라 가정하면,
- 35개의 데이터가 17개씩 나눠짐 -> 2조각이 된다.
- 이어서 8개씩 나뉘어짐 -> 4조각이 된다.
- 이어서 4개씩 나뉘어짐 -> 8조각이 된다.
- 이어서 2개씩 나뉘어짐 -> 16조각이 된다.
- 이어서 last, 1개씩 나뉘어짐 -> 32조각이 된다.
위를 보면 총 5번의 분할 과정이 일어났다.
그러면 이번엔 데이터가 31개라 가정하자.
- 31개의 데이터가 15개씩 나뉘어짐 -> 2조각
- 이어서 7개씩 나뉘어짐 -> 4조각
- 이어서 3개씩 나뉘어짐 -> 8조각
- 이어서 1개로 나뉘어짐 -> 16조각
.. 분명 뭔가 규칙성이 있을거다.
위의 31과 35의 과정을 보면, 32(2^5)을 기준으로 한번의 분할과정 차이가 생긴다.
여기서 둘로 나뉘는 분할 횟수를 k, 데이터 개수는 n이라 치면
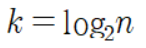
가 된다.
한번 분할되었을 때 일어나는 비교연산은 n, 총 분할 횟수가 k이면,
빅-오는 k * n. 즉
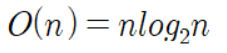
이 된다.
이 Quick Sort는 최선의 경우로 생각했지만, 최악의 경우로 따지면 n^2이 된다. 그런데 이 퀵 정렬은 실제로 진행해보면 n^2보단 nlog2n에 가까운 결과를 보이기에 최선의 경우로 따진 빅-오가 이 정렬의 성능이라고 보는게 더욱 부합하다.
여기까지
오늘은 컨디션이 넘모 별로라, 이정도만 하겠다.