오늘은 정렬 Ch 에서 마지막으로 남은 Radix Sort(기수 정렬)을 복습 하고, 이후에 Ch.11을 따로 복습한 글을 올리겠다.
Radix Sort (기수 정렬)
우선, "기수"란 말이 생소할 수도 있다.
- 기수(radix) : 데이터를 구성하는 기본 요소
만약 10진수가 0, 1, 2, 3, 4, 5, 6, 7, 8, 9로 이루어져 있으면, 이 10개의 숫자가 10진수의 "기수"가 되는 것이다.
이 기수를 이용해서 정렬하는 방법이 기수 정렬이다.
이 기수 정렬은 다른 정렬들과 눈에 띄게 독보적인 장점이 하나 있다.
"정렬 순서상 앞서고 뒤섬의 판단을 위한 비교연산을 하지 않는다"
?
우린 지금까지 여러 정렬들을 살펴보면서, 성능평가, 즉 시간복잡도 계산을 할 때에 비교연산을 핵심 요인중 하나로 픽 했었다. 그런데 이를 하지 않는다는건, 어마무시한 메리트가 있다.
그런데, 어마무시한 메리트가 있는만큼의 단점이 있다.
"적용할 수 있는 범위가 제한적" 이란 거다.
데이터의 길이가 같은 데이터들을 대상으로는 정렬을 할 수 있으나, 길이가 같지 않으면 정렬이 불가능하다. 데이터 길이가 다른 데이터들을 가지고 정렬을 하려면 별도의 알고리즘을 따로 넣어줘야 한다. 그런데, 이 별도의 알고리즘도 또 효율을 따져줘야하니, 상당히 귀찮아진다.
만약, 10진수로 이루어진 배열인 "6 / 5 / 3 / 8" 네가지 요소를 정렬을 한다고 치자.
그러면 0 ~ 9까지 10개의 "bucket(양동이)"를 마련해서, 각각 본인의 숫자에 해당되는 양동이에 숫자를 넣는다. 그 다음, 이를 sortArr 로 옮긴다.
이 기수 정렬의 구현을 하는데에는 2가지 방법이 있다.
1. LSD (Least Significant Digit)
"덜 중요한 정수". 즉, 첫번째 자릿수부터 시작해서 정렬을 진행한다는 얘기다.
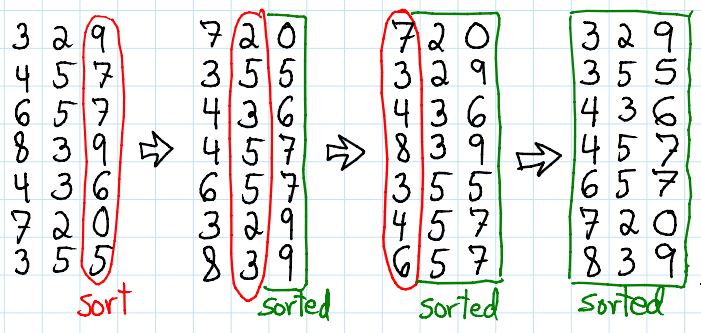
이렇다는 얘기다. 첫번째 자릿수를 기준으로 정렬 -> 첫번째 자릿수로 정렬된 대상을 기반으로 두번째 자릿수를 기준으로 정렬 -> 두번째 자릿수로 정렬된 대상을 기반으로 세번째 자릿수를 기준으로 정렬.
얘는 작은 자릿수부터 큰 자릿수까지 모두 비교를 해야 "만" 값의 대소를 판단할 수 있다.
근데 의문이 들 수도 있다.
우린 보통 354 vs. 267 이라는 두 정수를 비교한다고 치면 그냥 맨 앞에 백의 자리수인 3과 2만 봐도 대소 비교가 되는데, 왜 굳이 작은 자릿수부터 큰 자릿수까지 싹~~다 비교를 하면서 값의 대소를 판단할까?
일단, 다른 방식 하나도 보자.
2. MSD (Most Significant Digit)
위의 LSD와 반대다. 가장 큰 자릿수의 숫자부터 정렬을 진행한다.
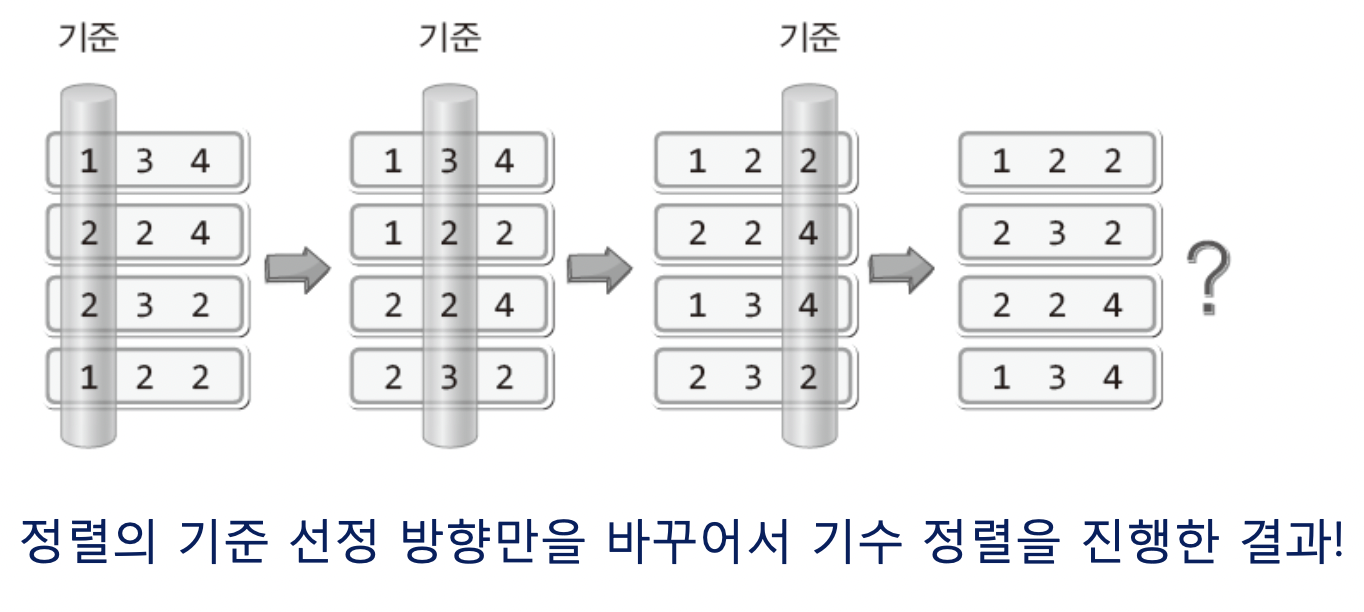
..? 딱봐도 마지막 결과가 이상하지 않나?
224와 232의 대소비교는 첫번째 화살표가 지나고 멈췄어야 했다.
이렇게 중간에 정렬이 완료될 수도 있다는 장점때문에, "모든 데이터에 일괄적인 과정을 거치게 할 수 없다"는 단점이 생긴다.
..이래서, 우리는 "LSD"를 사용할거다.
MSD는 모든 데이터에 일괄적 과정을 거치게 할 수 없어서, 추가적인 연산과 별도의 메모리를 요구한다. 그냥 LSD를 사용해서 맘편하게 처음부터 끝까지 비교를 하는게 낫다. 어짜피 LSD와 MSD의 빅-오는 같으니까.
기수 연산에 대한 코드는 아래에 작성해놓겠다.
#include <stdio.h>
#include "ListBaseQueue.h" // 버킷의 구조가 큐에 해당함
#define BUCKET_NUM 10
void radixsort(int arr[], int num, int maxLen) {
// maxLen 은 정렬 대상중 가장 긴 데이터의 길이 정보가 전달
Queue buckets[BUCKET_NUM];
int bi, pos, di, radix;
int divfac = 1;
for (bi = 0 ; bi < BUCKET_NUM ; bi++) {
//버킷 초기화
QueueInit(&buckets[bi]);
}
for (pos = 0 ; pos < maxLen ; pos++) {
// 가장 긴 데이터 길이만큼 반복
for (di = 0 ; di < num ; di++) {
radix = (arr[di] / divfac) % 10; // N번째 자리 숫자 추출
Enqueue(&buckets[radix], arr[di]);
}
for(bi = 0, di = 0 ; bi<BUCKET_NUM ; bi++) {
// 버킷 수만큼 반복
while(!QIsEmpty(&buckets[bi]) {
arr[di++] = Dequeue(&buckets[bi]);
// 버킷에 저장된 순서대로 꺼내서, 다시 arr로 옮김
}
}
divfac *= 10; // for문 내 첫번째 for문에서 N번째 숫자 추출 위함
}
}
.
.
.여기에선 maxLen을 통해 길이가 다른 친구들도 연산을 가능하게 만들었다.
성능 평가
여기에선 앞서 언급한것처럼 비교 연산이 핵심이 아니다. 오히려, 버킷에 데이터를 넣고 빼는것을 핵심으로 잡아야하지 않나.
위의 for문 두개가 핵심이 될거다.
이 for문 두개 (데이터 삽입 / 데이터 추출)를 한 쌍으로 묶으면,
maxLen * num
이 될건데, 정렬대상의 길이가 L, 정렬대상 수가 num이면
L * num.
즉 빅-오는 O(ln). 결과적으로 O(n)이 된다.
정말 효율적이긴 하지만, 적용 가능한 대상이 제한적이란걸 유의하고 알아두자.