Ch.12 탐색(Search) 2
이번에도 "탐색" 과 관련된 내용을 학습하는 Chapter지만, 앞서 이진 탐색 트리의 연장선상이라고 봐도 된다.
12-1
앞서 이진 탐색 트리는 트리 높이 +1 당 추가할 수 있는 노드의 수가 2배씩 늘어나서, O(log2n)의 시간 복잡도를 가졌었다.
하지만, 아래와 같은 경우에도 그럴까?
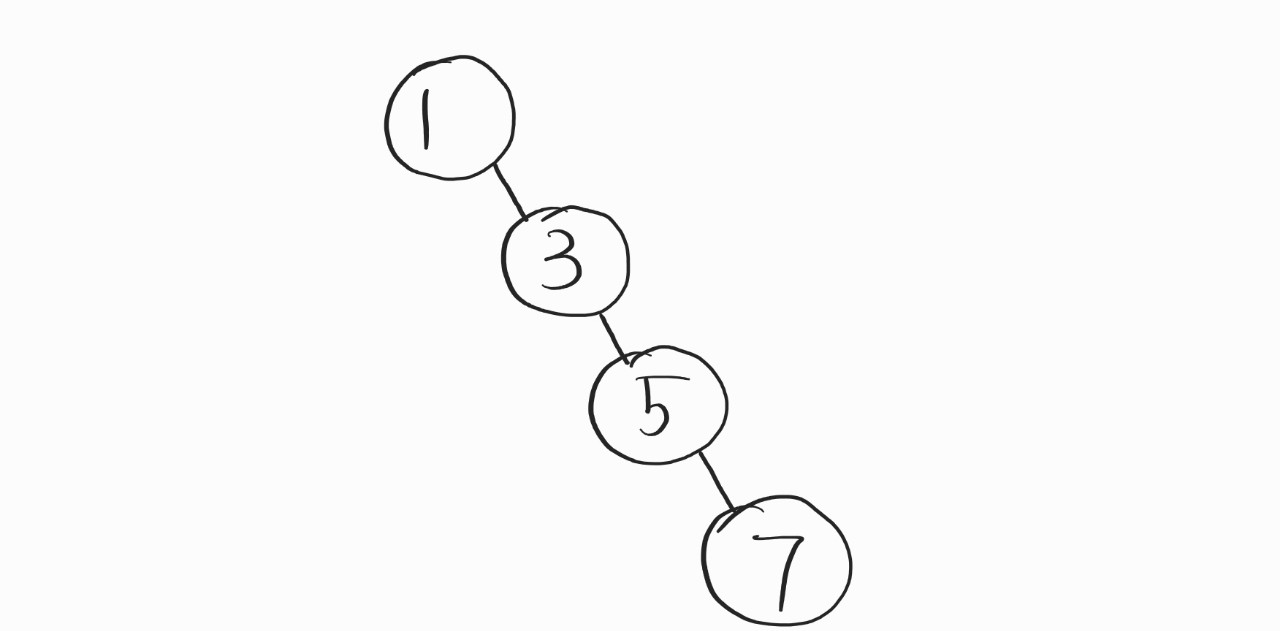
이 트리는 불균형한 이진 탐색 트리의 모습을 보이는데, 앞서 빅-오의 log2n과는 거리가 멀어보이는, O(n)의 양상을 보인다.
앞서 공부를 해서 얻게 된 지식으로는, O(n)과 O(log2n)은 어마무시한 차이를 가지고 있다.
만약 여기서 3이나 5를 먼저 저장을 하기만 했어도
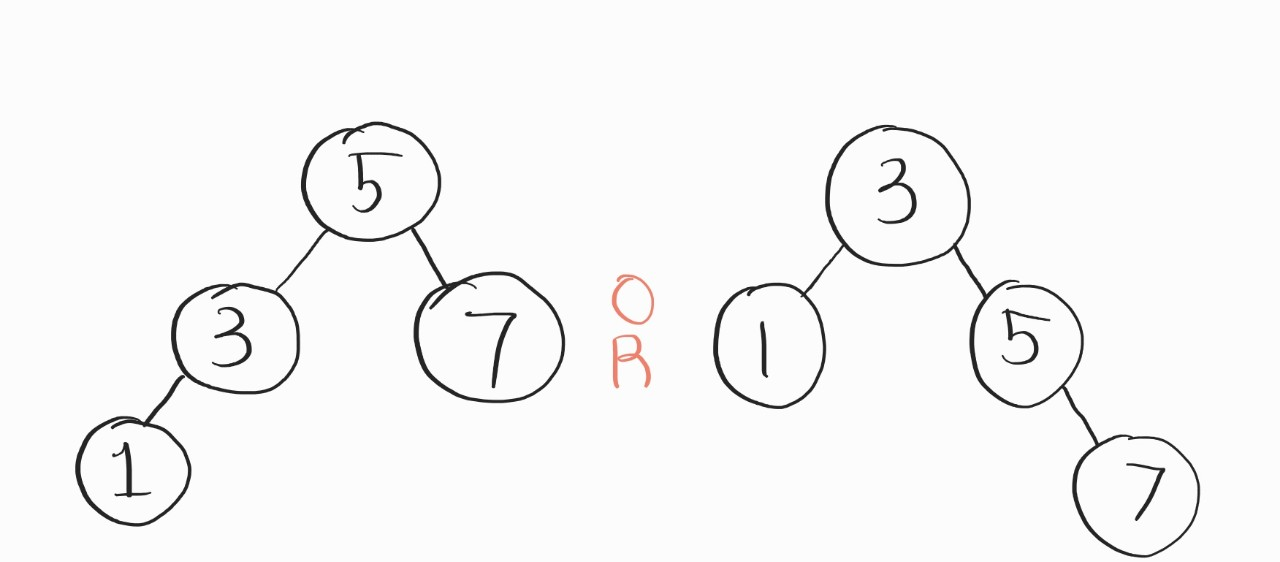그나마 나아졌을 거다.
이 예시를 통해서 Ch.11에서 복습한 이진 탐색 트리의 단점을 눈치챘는가?
데이터 저장 순서에 따라 탐색의 성능에 큰 차이를 보인다.
라는 것이다. 그냥 우리가 순서고 자시고 1-3-5-7 저장만 하면 바로 위의 그림처럼 알아서 판단해서 균형을 잡아줬으면 좋겠는데.
이제 그런 예시들을 공부할거다.
책에서 언급하기론 Red-Black tree, B tree.. 뭐 많은데,
우리는 이 중에서 AVL tree를 알아보기로 한다.
AVL TREE
노드가 추가될 때, 삭제될 때 트리의 균형상태를 파악해서, 스스로 그 구조를 변경해서 균형을 잡는 Tree다.
여기서 균형을 잡는데는 그 판단하는 기준이 필요할거다. 물론 그게 있고.
그 기준을 균형 인수(Balance Factor)라고 한다.
이 균형인수는 왼쪽 서브 트리 높이 - 오른쪽 서브 트리 높이다.
말로하면 뭔 소린지 모르니까, 그림을 보자.
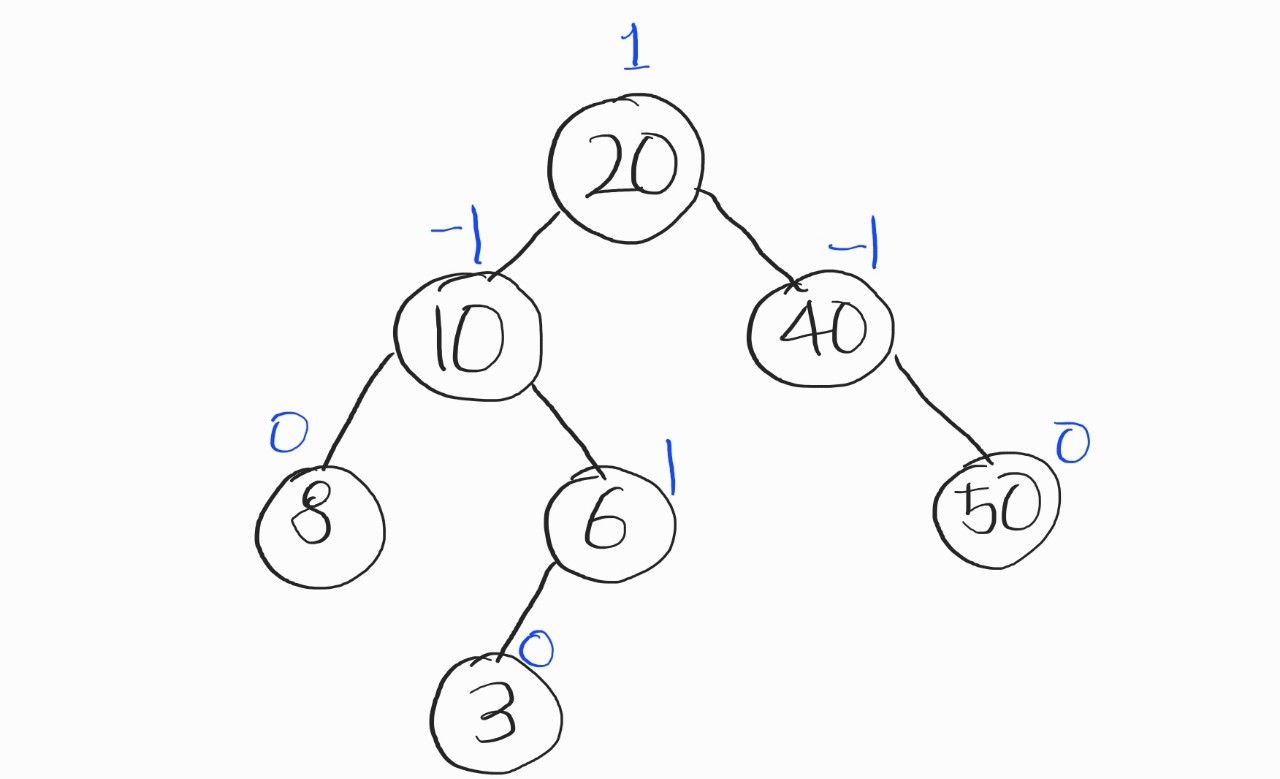
위의 파란 숫자가 균형인수다.
위의 그림은 어느정도 균형이 잡혀있는 상태다. 한 층 밖에 차이가 안나니까.
균형인수의 절댓값이 2 이상일 때 (x >= 2, x <= -2) 트리의 재조정, 즉 균형잡기를 진행한다.
이 "균형이 잡혀 있지 않은" 경우는 총 네가지의 경우가 있다.
1. LL상태
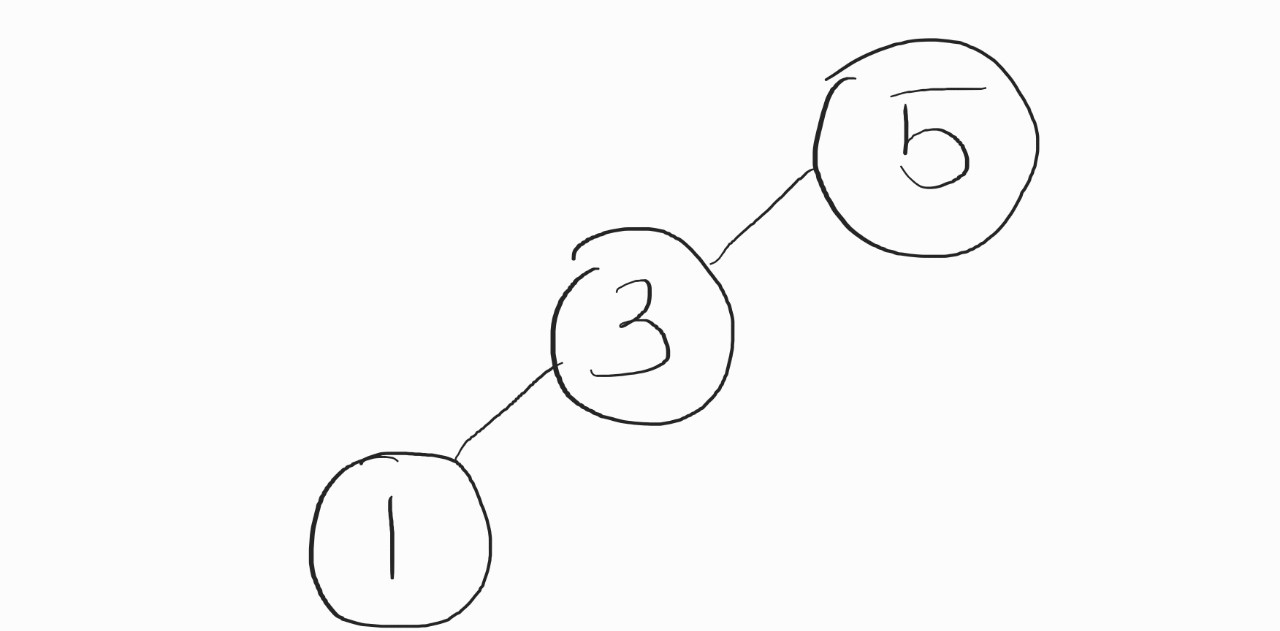
루트노드를 기준으로 왼쪽으로 두개 (Left로 두개니까 Left Left라 생각하자)로 왼편으로 치우쳐져 있다. 그래서 Left Left 상태, 즉 LL상태라고 한다. 위의 그림에선 어떻게 해줘야겠는가.
LL상태를 해결하기 위한 방법의 LL회전을 진행해주면 된다.
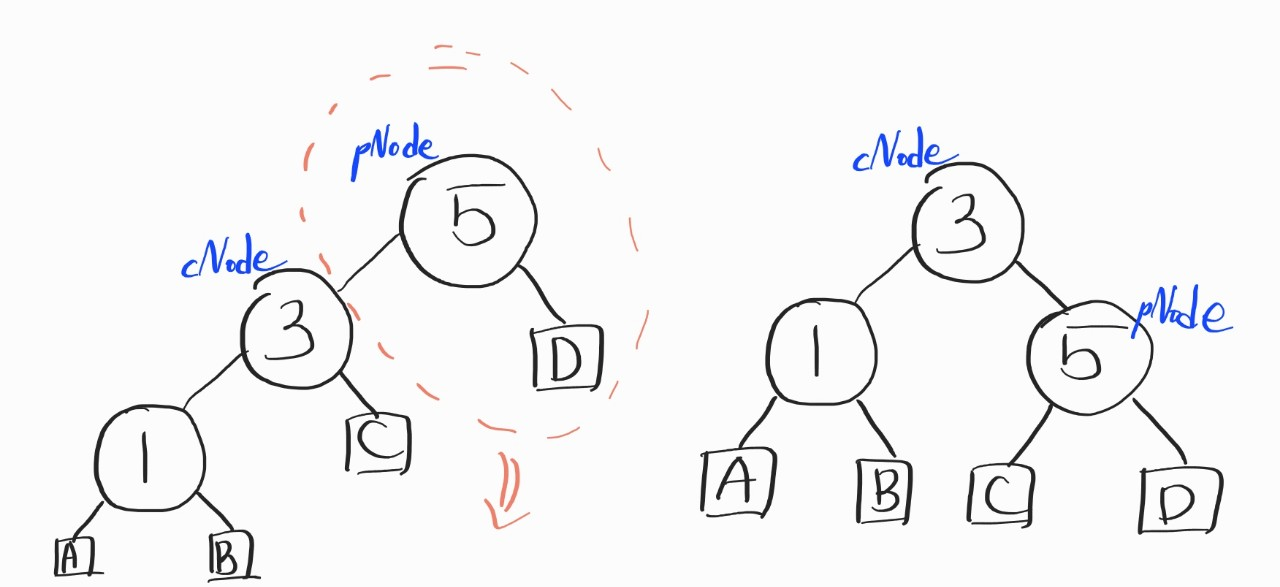
이렇게 해주면 된다. 위의 그림에서 생략한게 있는데, 저 네모 노드를 생략했다. 네모노드는 단말노드로 존재하는 자식노드들이라고 생각하면 됨.
이 과정을 말로 풀어주면
cNode의 오른쪽 자식노드를 pNode의 왼쪽 자식노드로 연결해줌 → pNode를 cNode의 오른쪽 자식노드로 연결해줌
ChangeLeftSubTree(pNode, GetRightSubTree(cNode));
ChangeRightSubTree(cNode, pNode);이렇게, 해주면 된다.
2. RR상태
그냥, 1번의 반대임.
Right Right로 불균형인 상태다.
이걸 해결하는 방법은 RR회전이고.
기본 형태와 RR회전을 바로 보여주겠다.
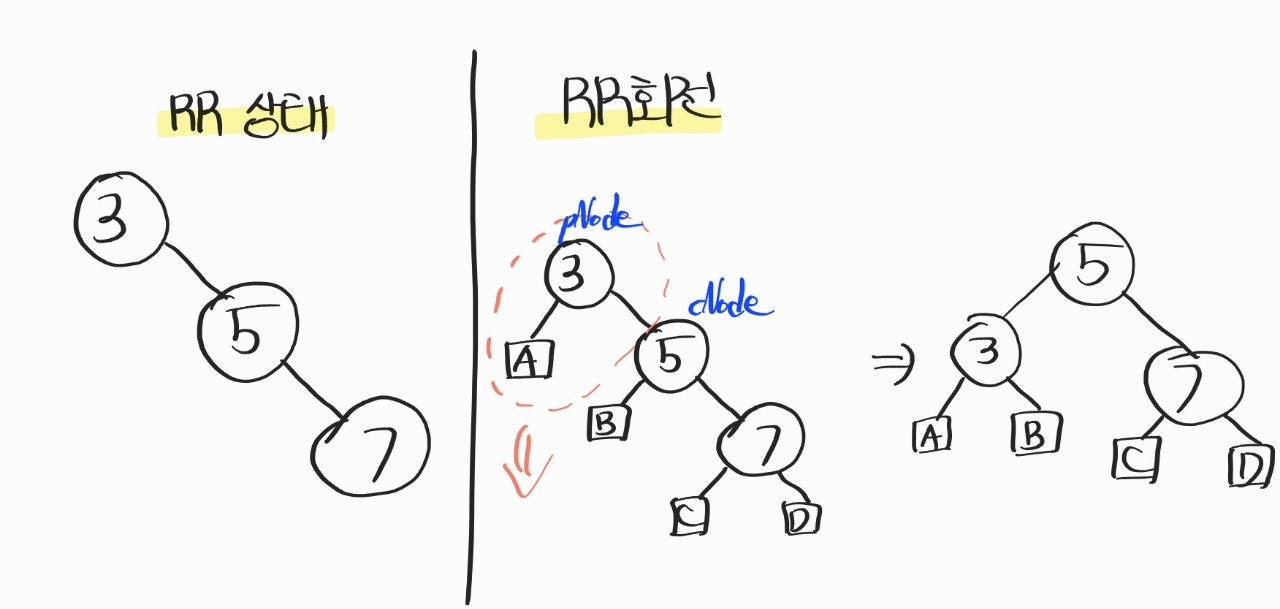
cNode의 왼쪽 자식노드를 pNode의 오른쪽 자식노드로 연결해줌 → pNode를 cNode의 왼쪽 자식노드로 연결해줌
ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
ChangeLeftSubTree(cNode, pNode);그렇다.
3. LR상태
이번엔 앞선 1번 2번과 조금 차이가 있다.
그래도, 앞서 LL상태와 RR상태의 이름과 기본 이론을 보면 대충 느낌이 오지 않나?
L-R 형태로 불균형이겠네. 그러면 루트노드 - 왼쪽자식노드 - 오른쪽자식노드로 꺾여있나?
맞다! 그냥 이렇게 생각해주면 된다.
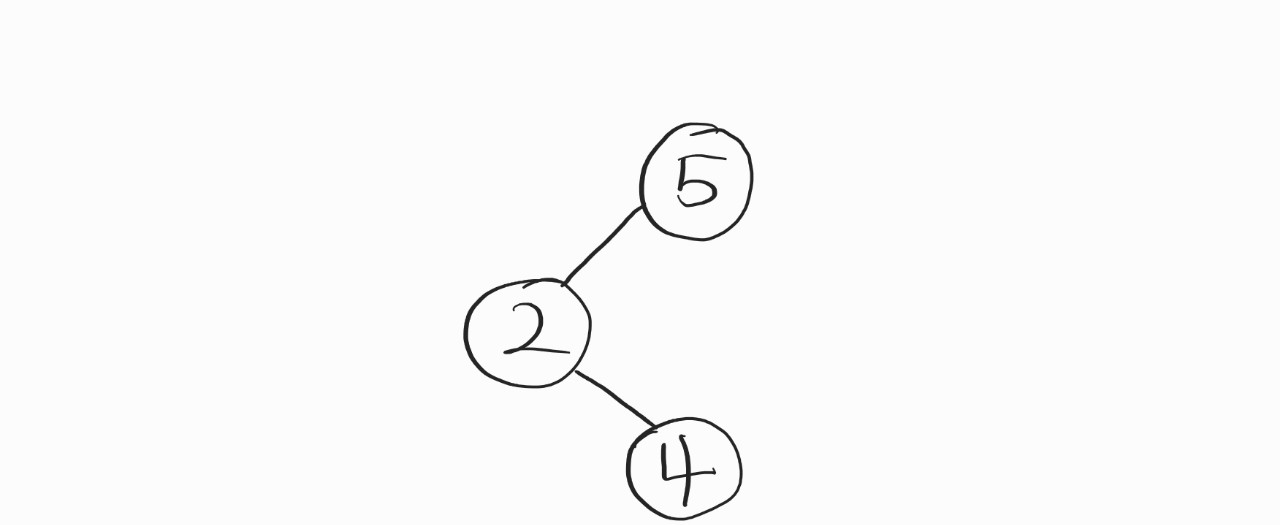
근데, 보기만 해도 조금 피곤하지 않나..?
앞선 친구들은 그래도 순서라도 맞았는데, 이건 순서도 좀 엮여있다. 우리가 생각한 대로라면 2-4-5가 배치되어야하는데, 왼쪽자식노드"의 오른쪽자식노드"가 섞여있으니까..
물론, 이걸 해결하기 위한 방법의 이름은 LR회전이겠지만, 조금 감이 안 잡힐수도 있다.
하지만, 별거없다!
우선, 그림으로 보자.
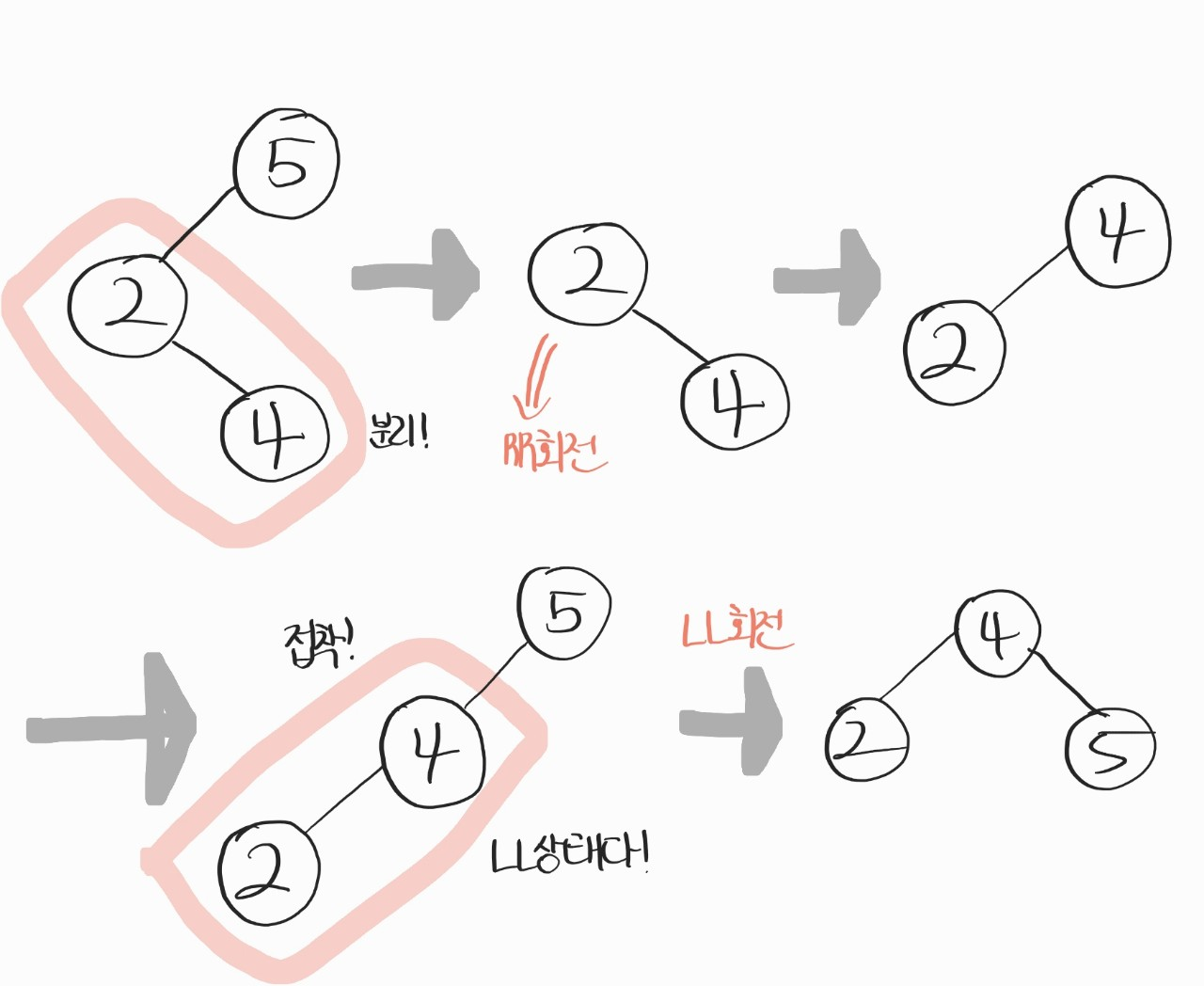
우선, 윗줄을 보면 루트노드를 제외한 두개의 노드를 분리해서, 부분 RR회전을 해준다. 그러면 한 파츠가 뚝딱!
그 다음, 부분 RR회전을 해준 서브트리를 다시 원래 있던 자리에 붙인다.
그러면 2 - 4 - 5의 그림이 익숙하지 않나? LL상태가 된다. 그러면 여기서 LL회전을 진행해주면, 우리가 원하는 균형있는 상태로 뚝딱!
이걸 그대~로 코드로 나타내주면 된다.
// 위의 그림에서 5가 pNode, 4가 cNode다.
//RRturn, LLturn은 각각 RR회전, LL회전을 나타내는 함수다.
ChangeLeftSubTree(pNode, RRturn(cNode));
LLturn(pNode);4. RL상태
뭐 굳이 따로 크게 적을 필요가 없다. LR상태의 반대임.
루트노드 제외 두개 노드 분리 → 부분LL회전 → 원래자리로 붙임 →루트노드 RR회전
이다.
ChangeRightSubTree(pNode,LLturn(cNode));
RRturn(pNode);12-2
이번엔 이 AVL 트리를 직접 구현해보도록 하자.
일단, 앞서 복습했던 내용들 중
이진 트리를 담은 헤더파일 / 소스파일과 이진 탐색 트리의 헤더파일 / 소스파일이 필요하다. Ch.08-2와 Ch.11-2를 참고하면 설명들이 있을거다.
근데 여기서 이진트리를 담은 파일에선, 뭐 딱히 확장을 할 기능이 없다.
BUT, 이진 탐색 트리의 파일에는 추가할게 하나 있다. 지금 우리가 AVL트리를 학습하면서 가장 핵심이라고 할 수 있는 "Rebalancing" 인데, 균형이 깨지는 과정은 데이터를 탐색할때 일어날까? 아니다. 데이터를 저장 / 삭제할 때 일어난다. 그래서 데이터를 저장하는 과정 / 데이터를 삭제하는 과정 에서 Rebalancing을 할 수 있게 해주면 따로 다른 기능을 추가 안해도 AVL 트리가 되기때문에, 이진 탐색 트리의 소스파일에 리밸런싱 기능을 추가한다.
( 리밸런싱 자체에 대한 기능은 따로 헤더파일과 소스파일을 만들거다. )
우선, 구현을 한다고 생각했을 때, AVL트리를 방금 배우면서 처음 뭘 판단했는지 보자.
균형인수의 절댓값이 2 이상일 때 불균형하다고 판단함.
그러면, 균형인수를 먼저 구해야하지않을까?
그런데, 균형인수를 구하려면 뭐가 필요하지?
균형인수 = 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
"트리의 높이"를 구할 수 있어야하네?
그러면 우선 트리의 높이를 구하는 함수를 짜보자.
// 높이를 반환해야하니 함수의 반환형은 int형
int GetHeight(BTreeNode *bst) {
int leftH; // 왼쪽 tree 높이
int rightH; // 오른쪽 tree 높이
if (bst == NULL) {
return 0;
}
leftH = GetHeight(GetLeftSubTree(bst));
rightH = GetHeight(GetRightSubTree(bst));
if (leftH > rightH) { // 왼쪽이 더 크면
return leftH + 1;
} else { // 오른쪽이 더 크면
return rightH + 1;
}
}왼쪽 오른쪽 다 갈수 있게하며 그 중 가장 깊이뻗은 경로를 찾아야하니까 재귀적으로 정의한다.
그러면, 이제 높이의 차이, 즉 균형 인수를 구할 수 있어야겠지?
int GetHeightDiff(BTreeNode *bst) {
int lsh, rsh; // 각각 left subtree height, right subtree height
if (bst == NULL) {
return 0;
}
lsh = GetHeight(GetLeftSubTree(bst));
rsh = GetHeight(GetRightSubTree(bst));
return lsh - rsh; // 균형인수를 반환함
}이렇게, 균형인수를 구하는 함수들은 다 정의를 끝마쳤다.
그러면 이번엔 뭘 해야할까?
불균형상태인건 앞의 함수들로 확인할 수있으니, 고쳐줘야지. LL / LR / RR / RL 회전을 구현할거다.
우선, 비교적 과정이 간단한 LL회전과 RR회전부터 보자.
BTreeNode * LLturn(BTreeNode *bst) {
BTreeNode *pNode;
BTreeNode *cNode;
pNode = bst;
cNode = GetLeftSubTree(pNode);
// LL회전
ChangeLeftSubTree(pNode, GetRightSubTree(cNode));
ChangeRightSubTree(cNode, pNode);
// LL회전으로 인해 변경된 루트노드의 주소값을 반환한다.
// 원래 pNode가 루트노드였다고 치면, 회전이후 cNode가 루트노드가 되니까
return cNode;
}BTreeNode * RRturn(BTreeNode *bst) {
BTreeNode *pNode;
BTreeNode *cNode;
pNode = bst;
cNode = GetRightSubTree(pNode);
// RR회전
ChangeRightSubTree(pNode, GetLeftSubTree(cNode));
ChangeLeftSubTree(cNode, pNode);
// RR회전으로 인해 변경된 루트노드의 주소값을 반환한다.
// 원래 pNode가 루트노드였다고 치면, 회전이후 cNode가 루트노드가 되니까
return cNode;
}핵심인 Change / Change 두 줄은 앞서 설명해서 큰 설명이 필요없을거다.
그러면 이번엔, LR회전과 RL회전이다.
BTreeNode *LRturn(BTreeNode *bst) {
BTreeNode *pNode;
BTreeNode *cNode;
pNode = bst;
cNode = GetLeftSubTree(pNode);
ChangeLeftSubTree(pNode, RRturn(cNode)); // 부분적 RR회전
return LLturn(pNode); // LL회전
}여기선 회전의 두번째 과정인 LL회전을 LLturn과 함께 바로 그 주소값을 반환해버린다. 굳이 따로 나눌 필요 없으니까..
앞의 이론 설명에선 나누고 / 부분회전 / 붙이고 / LL회전 이렇게 과정을 거쳤는데.
나누고 / 부분회전 / 붙이고를 ChangeLeft..에서 끝내고, 마지막 LL회전을 끝냄과 동시에 바뀐 루트노드의 주소값을 반환하는것이다.
RL회전은 그냥 앞에꺼 반대로.
BTreeNode *RLturn(BTreeNode *bst) {
BTreeNode *pNode;
BTreeNode *cNode;
pNode = bst;
cNode = GetRightSubTree(pNode);
ChangeRightSubTree(pNode, LLturn(cNode)); // 부분적 LL회전
return RRturn(pNode); // RR회전
}이제 이진 탐색 트리의 Insert와 Delete에 넣어줄 Rebalance 함수만 만들면, 준비가 끝난다.
기본 도구들은 앞서 다 마련되었으니까.
불균형을 판단하고.. 상태에 따라 회전해주고.. 이걸 합쳐보자!!
BTreeNode *Rebalance (BTreeNode **pRoot) {
int hDiff = GetHeightDiff(*pRoot); // 균형 인수
// 균형인수가 1보다 크다. 즉, 왼쪽이 불균형하다.
if (hDiff > 1) {
if (GetHeightDiff(GetLeftSubTree(*pRoot)) > 0) { // LL상태
*pRoot = LLturn(*pRoot);
} else { // LR상태
*pRoot = LRturn(*pRoot);
}
}
// 균형인수가 -1보다 크다. 즉, 오른쪽이 불균형하다.
if (hDiff < -1) {
if (GetHeightDiff(GetRightSubTree(*pRoot)) < 0) {
*pRoot = RRturn(*pRoot);
} else {
*pRoot = RLturn(*pRoot);
}
}
return *pRoot;
}그러면 이걸, 이진탐색트리의 BSTInsert와 BSTRemove에 넣어야 하는데, 어떻게 넣을까?
BSTRemove는 맨~~ 마지막쯤 삭제된 dNode를 반환하는 return dNode; 의 바로 앞에 *pRoot = Rebalance(pRoot); 만 넣어주면 된다.
그런데, BSTInsert는 좀 많이 바꿔줘야할 필요가 있다.
만약 BSTRemove처럼 리밸런스만 띡 넣어주면, 아래의 상황에 대처가 안된다.
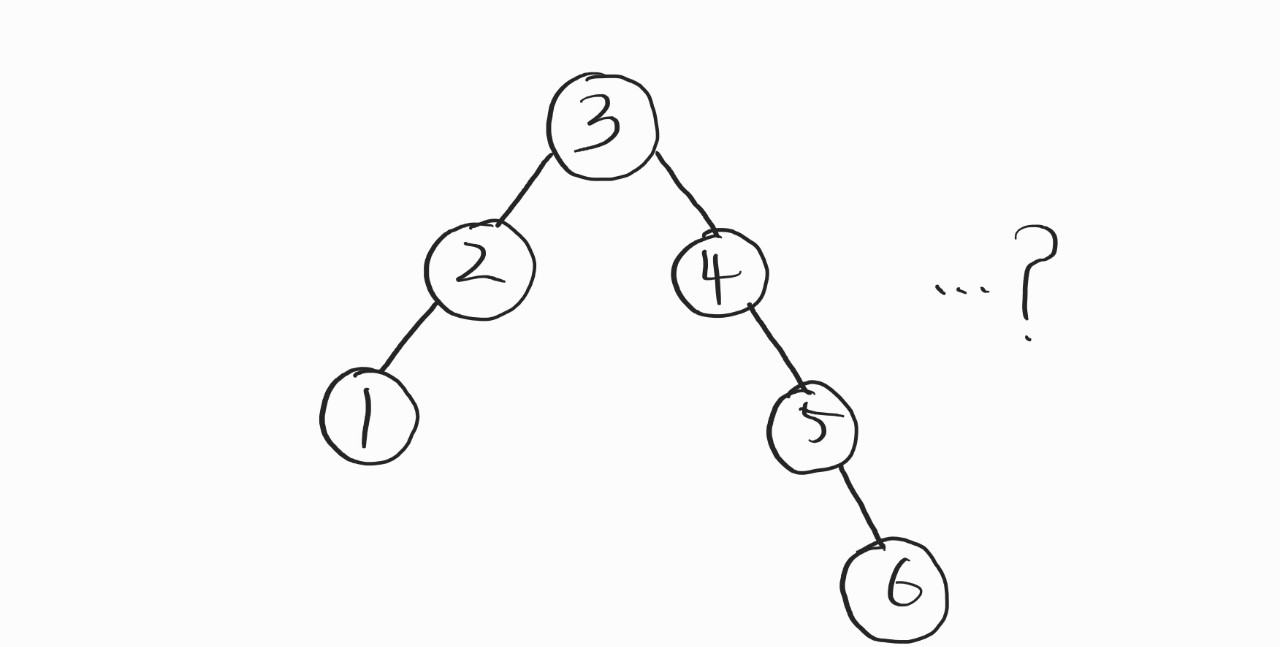
여기서 보면, 루트노드를 기준으로 그 어떤 회전을 하더라도 균형이 잡힐 수 없다.
균형이 잡히려면, 4-5-6을 RR회전을 해서 3의 우측에 붙여야 한다.
그러면, 여기선 불균형 여부를 어떻게 따지는가..
새로 저장된 노드(처음부터 순서대로 저장하면, 6이 새로이 저장되는 노드일 것이다.)의 부모 노드를 모~두 살펴야 한다. 즉, 위의 그림에선 5, 4, 3 모~든 부모 노드가 된다.
그렇게 나온 결과물 코드는 아래와 같다.
처음부터 새로 짜야한다.!
BTreeNode * BSTInsert(BTreeNode ** pRoot, BSTData data) {
// 루트노드를 대상으로 데이터 저장 TRY
if (*pRoot == NULL) { // 이 자리에 저장된 데이터가 없어!
*pRoot = MakeBTreeNode(); // 그 자리에 데이터 저장
SetData(*pRoot, data);
} else if (data < GetData(*pRoot)) { // 루트노드보다 데이터가 작아
BSTInsert(&((*pRoot)->left), data);
// &((*pRoot)->left)는 pRoot의 왼쪽 자식 노드의 주소값
*pRoot = Rebalance(pRoot);
} else if (data > GetData(*pRoot)) {
BSTInsert(&((*pRoot)->right), data);
*pRoot = Rebalance(pRoot);
} else {
return NULL; // 키의 중복을 허용하지 않는다.
}
return *pRoot;
}이렇다.
이제, 진짜 마지막. 메인함수를 살펴보자.
#include <stdio.h>
#include 이진트리 헤더파일
#include 이진탐색트리 헤더파일
int main() {
BTreeNode *avlRoot;
BTreeNode *clNode; // current left node
BTreeNode *crNode; // current right node
BSTMakeAndInit(&avlRoot);
BSTInsert(&avlRoot, 1);
.
.
. 대충 9까지 Insert
printf("Root Node : %d\n", GetData(avlRoot));
clNode = GetLeftSubTree(avlRoot);
crNode = GetRightSubTree(avlRoot);
.
. 쭉쭉 확인
return 0;
}이렇게 해서 루트노드를 확인해보면, 정상적으로 5가 나오고 양쪽으로 4개씩 쫙쫙뻗은 트리가 만들어질 것이다.
여기까지.
아 맞다.
풀버전의 소스파일(이진탐색트리 헤더, 소스 / 이진트리 헤더, 소스 / 리밸런싱 헤더, 소스)은 깃허브에 가면 있으니까, 여기서 확인하자.
