Ch.11 탐색 - 2일차
저번 시간엔 이진 탐색 트리의 아주 기본적인 기능들 (Insert, Search, Make&Init, GetData) 를 구현했었다.
그런데, 뭔가 나사가 하나 빠져있다는 생각이 안드는가.
"삭제" 기능 구현
삭제 기능이다.
앞서 구현한 기능들과 함께 구현해도 되었지만, 이번 삭제 과정은 신경써줄 부분이 많아서 꽤 코드가 복잡 / 길어지기 때문에. 저자가 따로 떼어놓은 듯 하다.
일단, 한번 삭제 과정을 살펴보자.
우선, 만약 어떤 트리에서 임의의 노드 하나를 삭제해야 한다고 가정하자.
그런데, 단순하게 노드 하나만 톡! 삭제하고 "삭제 끝!"이라고 할 수 있을까? 아니다. 어떤 노드를 삭제하면 그 부분이 빌 것인데, 그대로 빈 부분으로 놔두면 트리가 많이 망가지지 않을까? 노드 삭제 후에도 이진 탐색 트리가 유지되도록 누군가가 그 빈 자리를 대신 채워줘야 한다.
물론, 자식 노드가 없는 단말 노드의 경우에는 그냥 단순하게 삭제 과정만 진행해주면 된다.
하지만, 아래와 같은 경우라면?
- 자식 노드가 하나 이상이다.
곤란해질거다. 앞서 말한 "빈 자리를 대신 채워줘야" 하는 과정을 거쳐야되니까.
그러면, 이런 예외의 경우들을 모두 가정해서 코드를 짜줘야 한다.
- 자식 노드가 없는 단말 노드를 삭제해야한다.
- 삭제할 노드가 자식 노드가 하나를 가지고 있다.
- 삭제할 노드가 자식 노드를 양쪽 다(두개) 가지고 있다.
그럼 이렇게 각 case들을 구별해줬으니, 한번 각각 case별로 코드를 구현해보자.
1번 case
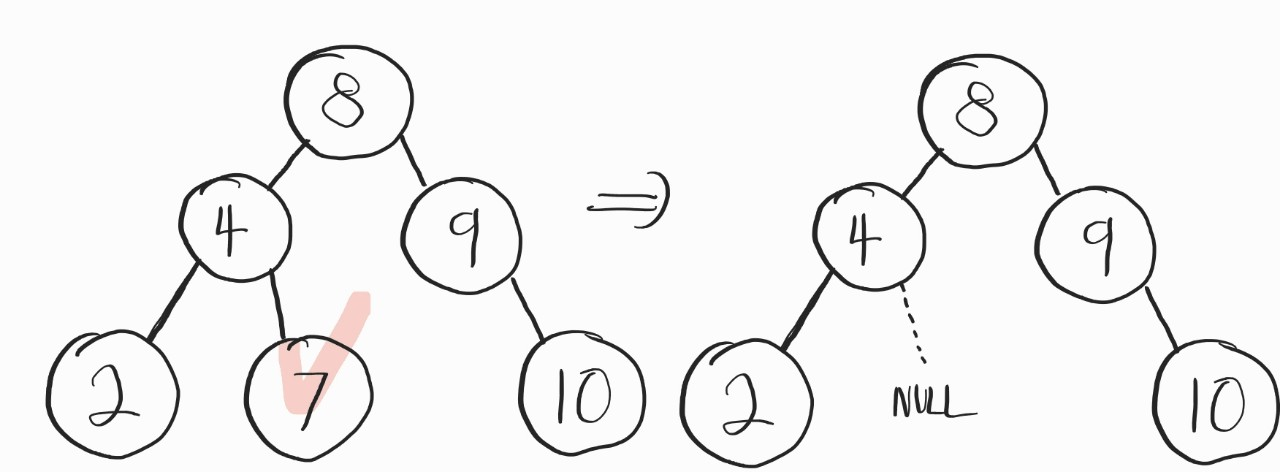
뭐 없다. 그냥 삭제만 하자.
그리고, dNode, cNode, pNode 이런 애들이 나올텐데,
dNode = 삭제할 노드
cNode = 현재 가리키고 있는 노드
pNode = dNode의 부모노드
이다.
if (GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL) {
if(GetLeftSubTree(pNode) == dNode) {
RemoveLeftSubTree(pNode);
} else {
RemoveRightSubTree(pNode);
}
}뭐 정말 별거 없다. 처음 보는 함수 Remove..SubTree가 있는데. 이건 해석한 그대로다. 왼 / 오른쪽에 있는 SubTree를 삭제한다.
2번 case
여기부턴 조금 피곤하다.
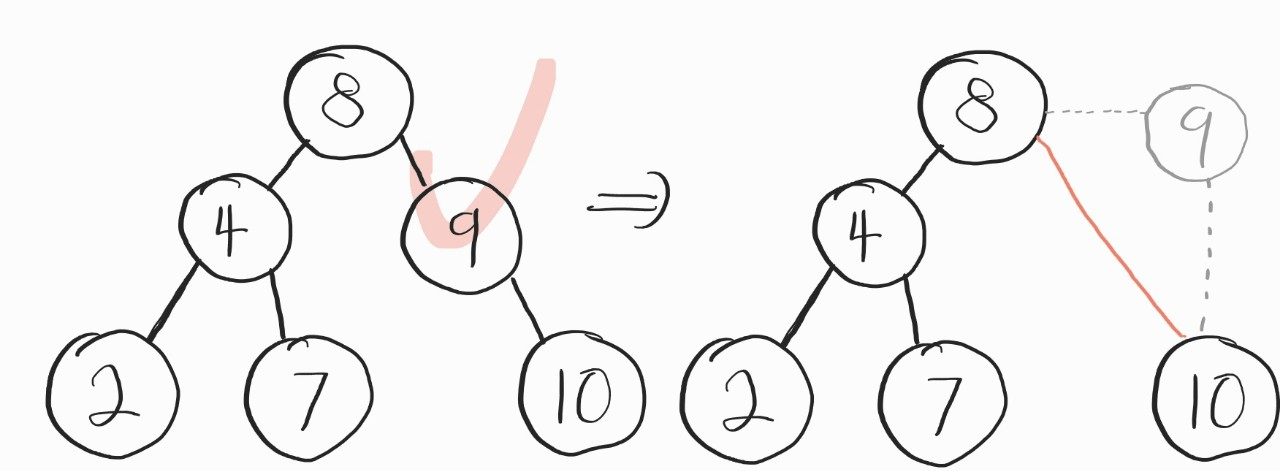
확실히 1번보단 몇 몇 과정이 더 붙는다.
삭제할 노드를 정한다 → 삭제할 노드의 부모노드와, 하나 남은 자식노드를 이어준다 → 본인은 떠난다
여기서 주의해야 할건, 9의 자식 노드인 10이 좌측의 자식노드이든 우측의 자식노드이든간에 그냥 무조건 10은 오른쪽 자식노드가 되어야한다는 점이다.
그냥 10이 9의 자리를 완전 "대체한다"고 생각하면 된다.
else if (GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL) {
BTreeNode *dcNode; // dNode의 child 노드
if (GetLeftSubTree(dNode) != NULL) {
dcNode = GetLeftSubTree(dNode);
} else {
dcNode = GetRightSubTree(dNode);
}
if (GetLeftSubTree(pNode) == dNode) { // 삭제 대상이 왼쪽 자식 노드면
ChangeLeftSubTree(pNode, dcNode); // pNode의 왼쪽으로 dcNode 연결
} else {
ChangeRightSubTree(pNode, dcNode);
}
}여기서 Change ~ SubTree(A, B) 함수는 "A의 ~쪽의 자식노드로 B를 연결시킨다" 라는 의미로 알고 있으면 되겠다. Make~SubTree와 매우 유사하다고 생각하자.
3번 case
문제의 3번 케이스다.
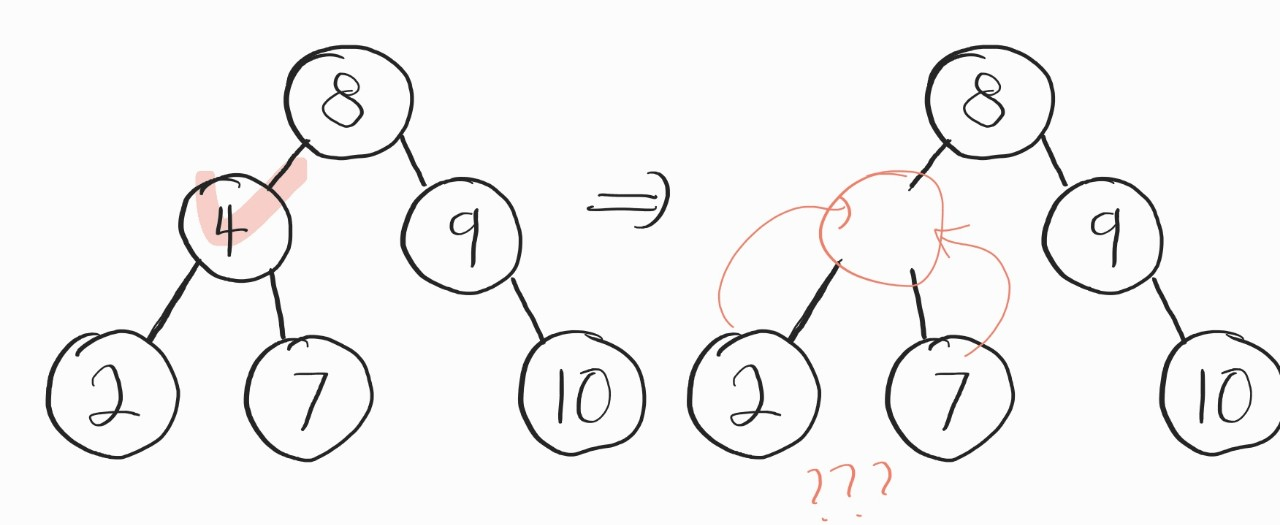
위의 1번, 2번 케이스의 경우엔 어떤 노드가 삭제가 된다면 무엇이 빈 자리를 대체해야할지 명확하게 알 수 있었는데, 이번엔 좀 다르다. 왼쪽과 오른쪽 중 뭐가 들어가든간에 맞는 선택이 된다. 어떻게 해야할까?
여기선, 그냥 원하는걸 넣으면 된다.
- 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 값
- 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값
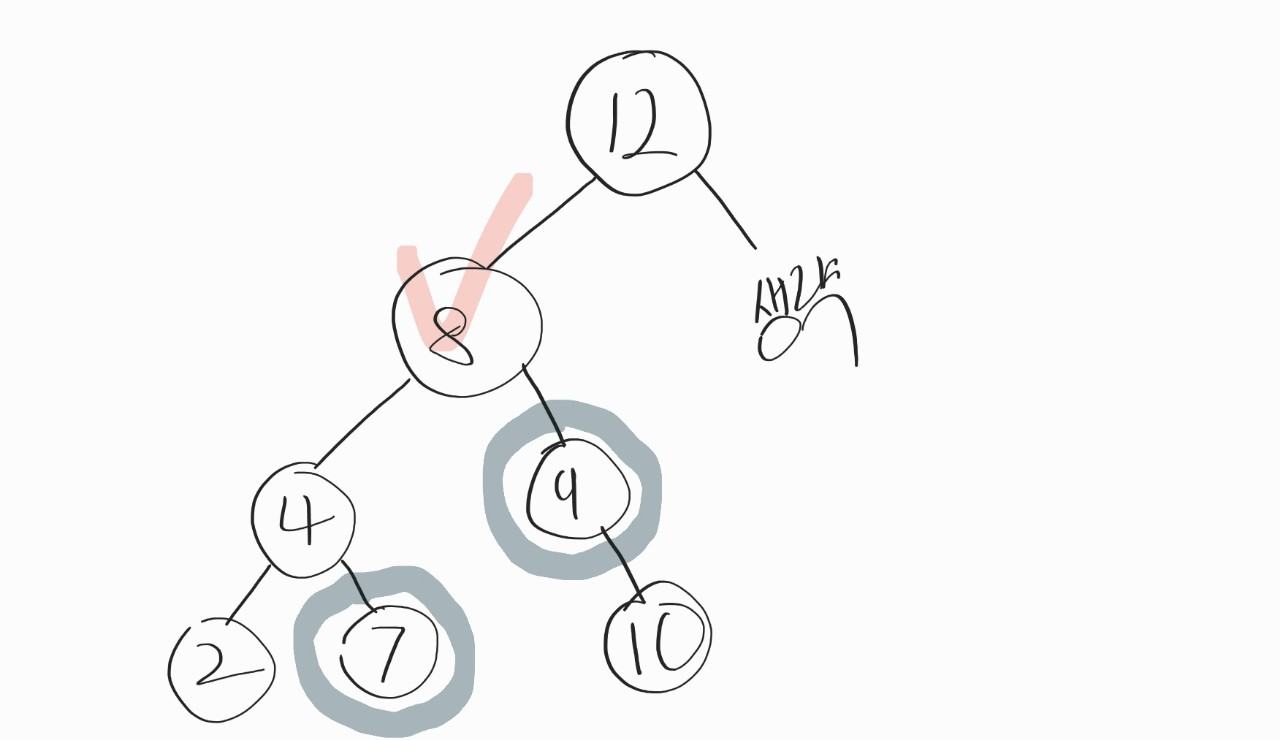
만약 위와 같은 상황이라면, 왼쪽에서 가장 작은 값인 7이 대체 노드가 되어도 되고,
오른쪽에서 가장 작은 값인 9가 대체노드가 되어도 된다.
그런데 이 두가지의 경우를 찾으려면 서브트리에서 가장 큰 값이나 가장 작은 값을 찾는 방법을 알아야 하는데, 뭐 어렵지 않다.
그냥 서브트리의 왼쪽 끝으로 직진하면 가장 작은 값이 나오고, (8을 기준으로 위의 그림에서 2), 서브트리의 오른쪽 끝으로 직진하면 가장 큰 값이 나온다. (8을 기준으로 위의 그림에서 10).
물론, 가장 큰값까지 찾을 이유는 없지만. 그냥 삭제할 노드의 바로 오른쪽 노드 (GetRightSubTree(dNode))를 기준으로 왼쪽 끝에있는 노드를 잡으면 되니까.
본서에서는 2번 방법, 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값을 대체 노드로 삼는다 하니, 이에 따라 구현해도록 해보겠다.
그러면, 위의 그림에 2번 방법을 적용하면 최종적으로 어떤 그림이 나올까?
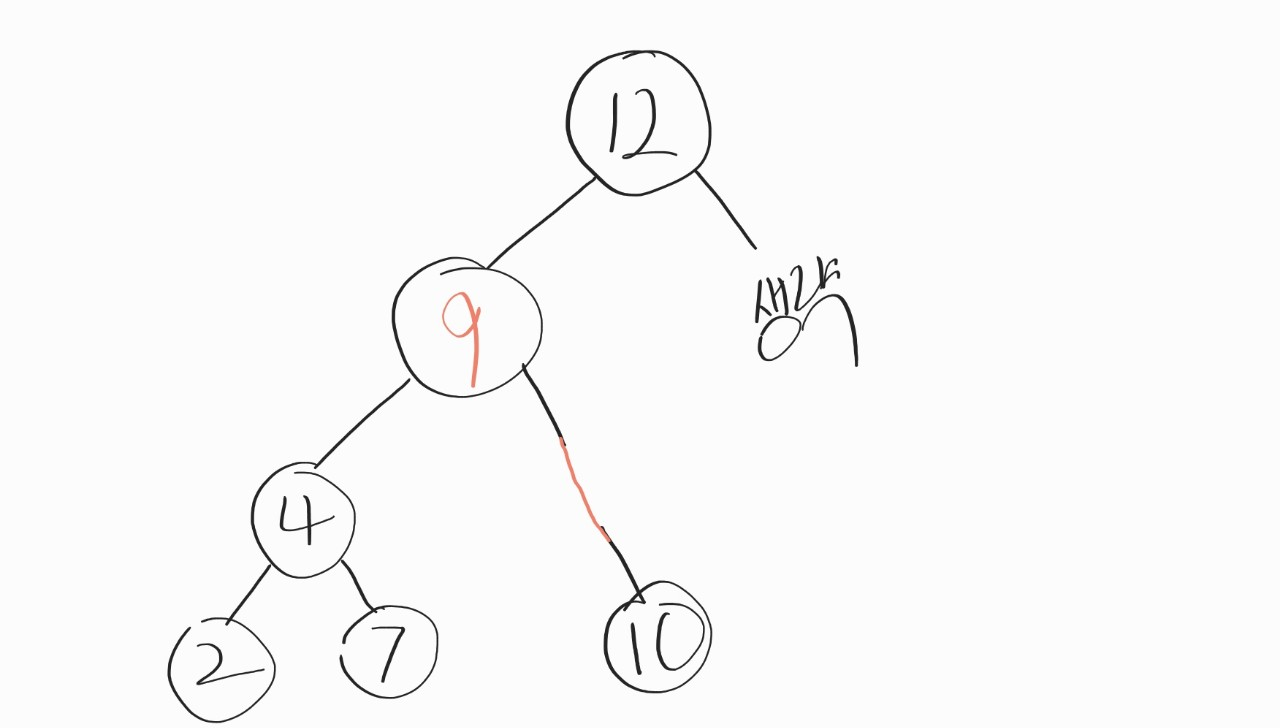
이런 그림이 나올꺼다.
과정은 이렇다.
삭제 대상 노드는 dNode, 대체할 노드(위의 그림에서 9)는 mNode라고 가정한다.
1st. mNode 선정 → 2nd.mNode의 값을 dNode에 대입 → 3rd.mNode를 비우고, mNode의 부모노드(dNode)와 mNode의 자식노드를 연결
이렇게 한다면, 삭제 대상의 부모 노드 (12) 까지 갈 필요가 없다. 만약 삭제 대상을 바로 지웠다면, 12 까지 손을 대줬어야 하니 괜히 한 과정을 늘리는 불상사가 생겼을 것이다.
그러면, 위의 세 단계에 따라 코드를 구현해보자.
.
.
.
else {
BTreeNode * mNode = GetRightSubTree(dNode); // 대체 노드
BTreeNode * mpNode = dNode; // 대체 노드의 부모 노드
int delData;
// 1. 삭제 대상(dNode)의 대체 노드(mNode) 검색
// mNode의 왼쪽 끝으로 간다. "우측 서브트리의 가장 작은 값"을 찾으니까.
while (GetLeftSubTree(mNode) != NULL) {
mpNode = mNode;
mNode = GetLeftSubTree(mNode);
}
// 2. 대체 노드(mNode)에 저장된 값을 삭제할 노드(dNode)에 대입
delData = GetData(mNode); // 백업
SetData(dNode, GetData(mNode));
// 3. 대체 노드의 부모 노드와 자식 노드를 연결
if (GetLeftSubTree(mpNode) == mNode) { // 만약 대체 노드(mNode)가 왼쪽 자식 노드 위치에 있다면
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode)); // 대체할 노드의 자식 노드를 부모 노드의 왼쪽에 연결
} else {
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
}
dNode = mNode; // 대체 노드를 삭제 노드 위치에 집어넣고
SetData(dNode, delData); // 백업데이터(delData)를 복원한다.
}
이런 식으로 코드를 짜주면 된다..
그런데, 여기서 의문이 드는 사람들이 있을거다. 본인처럼
// 3. 대체 노드의 부모 노드와 자식 노드를 연결
if (GetLeftSubTree(mpNode) == mNode) {
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
} else {
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
}여기를 보면, Change ~ SubTree의 우측 인자가 둘 다 GetRightSubTree다.
이게 좀 이해가 안 갈 수도 있는데, 왜일까?
..
바로..
바로...
대체할 노드(mNode)의 자식 노드는 항상 오른쪽에 존재하기 때문이다.
왜냐고?
만약 대체할 노드의 왼쪽 자식 노드가 있다면, 그 자식 노드가 mNode가 되어야 하는데, 어떻게 왼쪽에 존재할 수 있겠는가? 당장 아무 트리나 하나 그려보면, 이게 무슨말인지 알 것이다.
만약 굳이~ 이해가 안 된다면. 아래 트리가 위의 코드대로 삭제가 되는걸 보자.
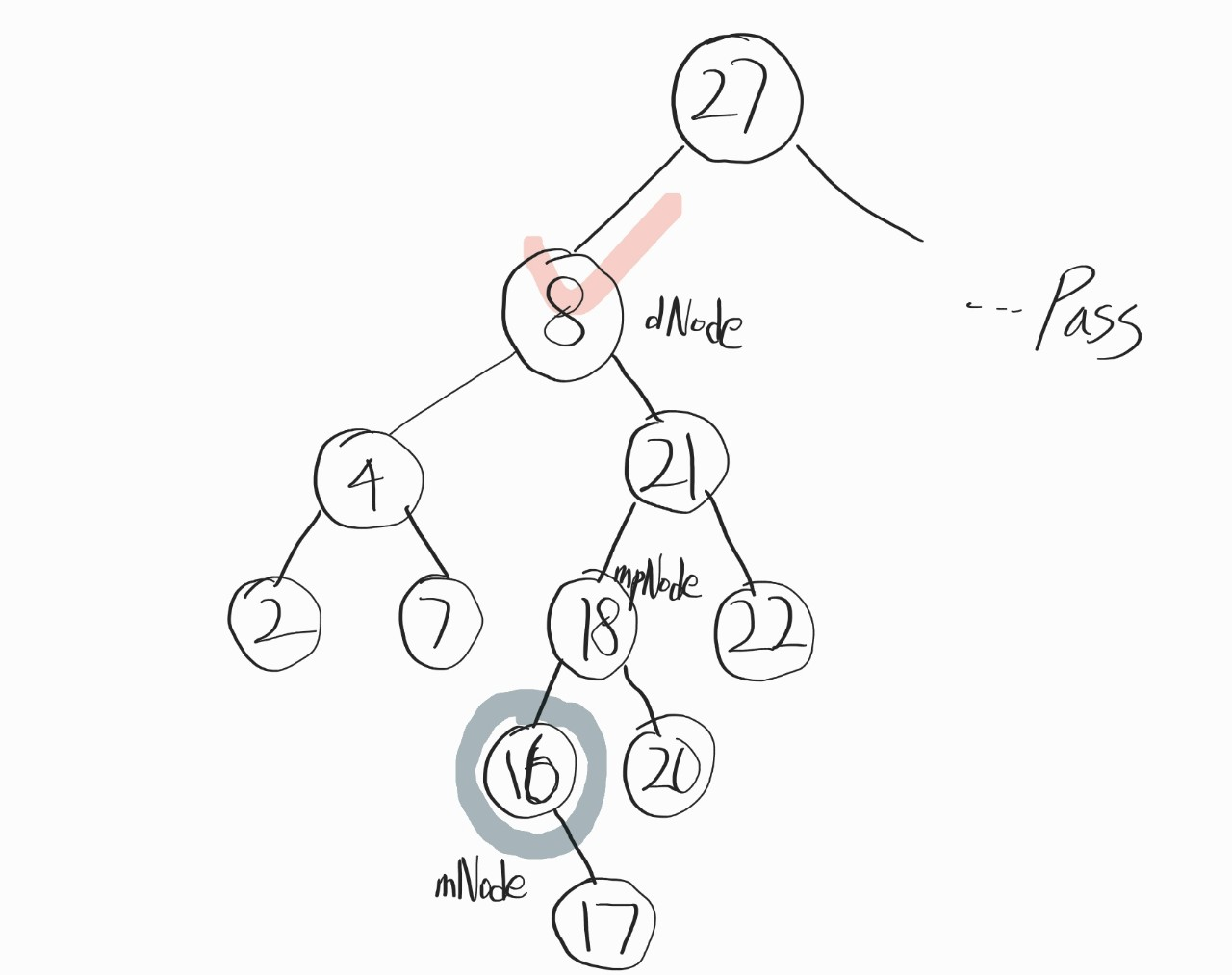
만약 여기서 mNode인 16의 왼쪽에 14라는 자식 노드가 있었다면, 애초에 걔가 mNode가 되었어야지.
만약 21 아래로 아무것도 없었다고 가정해도, 8의 자식 노드는 오른쪽 21이 mNode이고, 대체할 자식 노드는 NULL이 되니까, 코드대로 돌아가도 아무 이상 없다.
Understand?
솔직히 필자도 지금 복습하면서 좀 더 완전히 이해가 되는 것 같다
이정도면, 대충 60%정도 삭제를 구현한 것 같다.
부족한게 몇개 있으니, 그걸 보충해보자.
앞서 보면 Change~SubTree, Remove~SubTree 가 있는데, 설명을 안해줬다.
어짜피 Left든 Right든 그냥 큰 차이 없으니, Left를 기준으로만 설명을 하겠다.
// 왼쪽 자식 노드를 트리에서 제거.
BTreeNode * RemoveLeftSubTree(BTreeNode *bt);
// 메모리 소멸 없이 main의 왼쪽 자식 노드를 sub로 변경
BTreeNode ChangeLeftSubTree(BTreeNode *main, BTreeNode *sub);이 함수의 정의는
BTreeNode * RemoveLeftSubTree(BTreeNode *bt) {
BTreeNode * delNode; //삭제할 노드
if (bt != NULL) {
delNode = bt->left;
bt->left = NULL;
}
return delNode;
}
void ChangeLeftSubTree(BTreeNode * main, BTreeNode * sub) {
main->left = sub;
}뭐 굳이 설명이 필요없을 것 같다.
그리고, Remove의 경우에는 "제거" 한다고 해서 "메모리의 해제"까지 해주어야 할 것 같지만, 이는 아니다. 메모리의 해제를 해주지 않는 대신에, 삭제한 노드의 주소값을 delNode에 저장하여 반환한다.
Remove 함수의 완전체
거의 다왔다!!
마지막으로, 함수의 완전체를 보고, 앞서 설명에 없었던 친구들을 설명해주고 끝마치겠다.
이 설명에 없었던 친구들은 문장 뒤에 주석으로 따로 표기하겠다
// Here!!이렇게!
좀 많긴 한데, 이 부분만 찾아보고 싶으면 함수의 첫부분 / 끝부분만 보면 된다. 여기에 다있으니까.
BTreeNode *BSTRemove(BTreeNode ** pRoot, BSTData atrget) {
BTreeNode *pVRoot = MakeBTreeNode(); // Here!!
BTreeNode *pNode = pVRoot; // Here!!
BTreeNode *cNode = *pRoot; // Here!!
BTreeNode *dNode; // Here!!
ChangeRightSubTree(pVRoot, *pRoot); // Here!!
while(cNode != NULL && GetData(cNode) != target) { // Here!!
pNode = cNode;
if (target < GetData(cNode)) {
cNode = GetLeftSubTree(cNode);
} else {
cNode = GetRightSubTree(cNode);
}
}
if (cNode == NULL) { // Here!!
return NULL;
}
dNode = cNode; // Here!!
if (GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL) {
if(GetLeftSubTree(pNode) == dNode) {
RemoveLeftSubTree(pNode);
} else {
RemoveRightSubTree(pNode);
}
}
else if (GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL) {
BTreeNode * dcNode;
if (GetLeftSubTree(dNode) != NULL) {
dcNode = GetLeftSubTree(dNode);
} else {
dcNode = GetRightSubTree(dNode);
}
if (GetLeftSubTree(pNode) == dNode) {
ChangeLeftSubTree(pNode, dcNode);
} else {
ChangeRightSubTree(pNode, dcNode);
}
}
else {
BTreeNode * mNode = GetRightSubTree(dNode);
BTreeNode * mpNode = dNode;
int delData;
while (GetLeftSubTree(mNode) != NULL) {
mpNode = mNode;
mNode = GetLeftSubTree(mNode);
}
delData = GetData(mNode);
SetData(dNode, GetData(mNode));
if (GetLeftSubTree(mpNode) == mNode) {
ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
} else {
ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
}
dNode = mNode;
SetData(dNode, delData);
if(GetRightSubTree(pVRoot) != *pRoot) { // Here!!
*pRoot = GetRightSubTree(pVRoot);
}
free(pVRoot);
return dNode;
}생각보다 설명하지 않은 부분이 많아서 놀랬을거다.
우선, 함수의 첫부분.
BTreeNode *pVRoot = MakeBTreeNode(); // Here!!
BTreeNode *pNode = pVRoot; // Here!!
BTreeNode *cNode = *pRoot; // Here!!
BTreeNode *dNode; // Here!!
ChangeRightSubTree(pVRoot, *pRoot); // Here!!
while(cNode != NULL && GetData(cNode) != target) { // Here!!
pNode = cNode;
if (target < GetData(cNode)) {
cNode = GetLeftSubTree(cNode);
} else {
cNode = GetRightSubTree(cNode);
}
}
if (cNode == NULL) { // Here!!
return NULL;
}
dNode = cNode; // Here!!갑자기 뭔 개소리야~ 싶을수도 있다. 뭐가 너무 많이 추가되니까.
일단 처음에 설정한 BTreeNode형 포인터 변수 네개부터 보자.
저건 그냥 그림으로 설명하는게 빠르겠다.
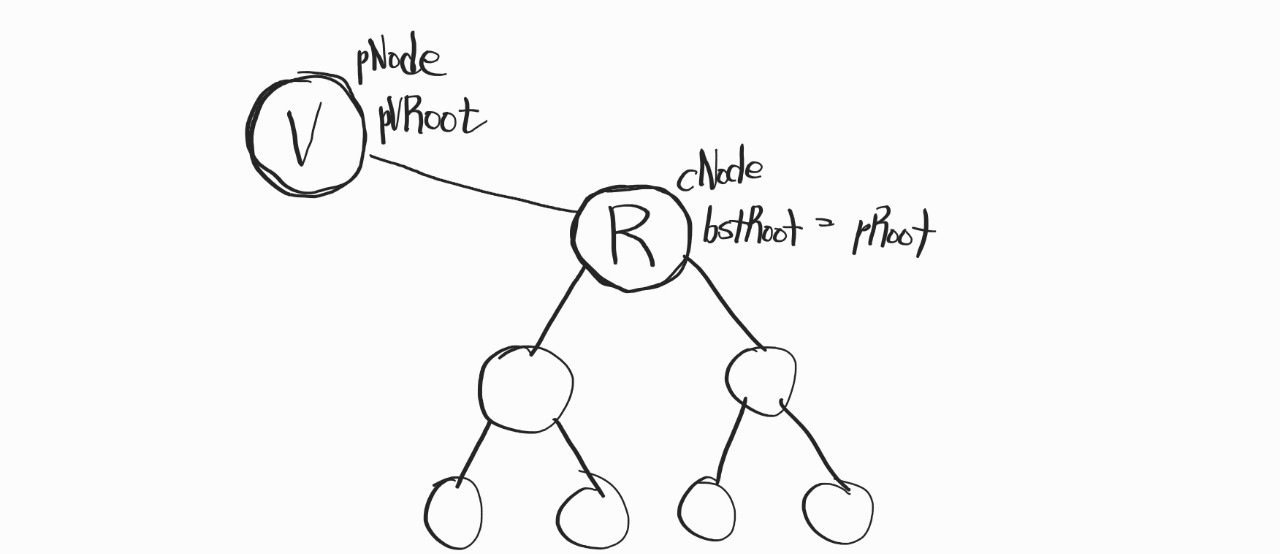
Remove 함수는 main 함수에서
BSTRemove(&bstRoot, 7) // bstRoot에 루트 노드의 주소값이 담겨있음처럼 전달받게 될텐데.
위의 V라는 가상의 루트 노드를 생성하여 "실제" 루트 노드인 R이 V의 오른쪽 자식 노드가 된다.
왜 굳이, 이런 가상 루트노드인 pVRoot 포인터 변수를 설정했을까?
"삭제할 노드가 루트 노드인 경우의 예외적 삭제 흐름을 일반화 하기 위함"
솔직히, 말이 좀 어렵다.
그런데 쉽게 말하면
"삭제할 노드가 루트노드일수도 있어요"
라는거다.
이 삭제과정이 진행되는동안 cNode와 pNode의 수직적 관계가 유지되어야하는데, cNode의 자식노드와 부모노드인 pNode를 연결시키는 과정이 등장하는 경우가 있기 때문이다. 위의 2번과정과 3번과정을 보면, 아하! 할거다.
근데 만약 가상의 루트노드가 없다면, 루트노드를 삭제해야 할 때 cNode와 pNode가 유지되지 않아서, 루트노드를 삭제하려면 일반적인 과정처럼 진행하기가 곤란해진다. 근데 이렇게 가상 루트노드를 선언하면 만사OK!
그 다음은
위에 보이는 while문과 if문인데
while(cNode != NULL && GetData(cNode) != target) { // Here!!
pNode = cNode;
if (target < GetData(cNode)) {
cNode = GetLeftSubTree(cNode);
} else {
cNode = GetRightSubTree(cNode);
}
}
if (cNode == NULL) { // Here!!
return NULL;
}
dNode = cNode; // Here!!쉽다. while문은 삭제 대상을 저장한 노드를 탐색하는 과정이다.
만약 앞의 조건인 cNode != NULL로 인해 탈출을 하게 된다면, cNode에는 NULL이 저장된다는 건데, 그러면 밑의 if문에 의해 "삭제할 대상이 없어요" 라는 의미로 NULL이 반환된다.
뒤의 조건인 GetData 어쩌구에 의해 탈출을 하게되면, cNode == target이라는 건데, 그러면 삭제할 대상의 위치를 찾았고, pNode엔 삭제할 노드의 부모 노드, cNode엔 삭제할 노드가 잡히게 된다. 그리고 dNode에 cNode를 저장해주면, 기본 세팅이 완료된다.
여기서 의문이 들 수도 있는게,
왜 BSTSearch 만들어놓고 안쓰세요
인데, 그러면 pNode를 설정할 수 없다.
그다음, Remove 함수의 마지막.
if(GetRightSubTree(pVRoot) != *pRoot) { // Here!!
*pRoot = GetRightSubTree(pVRoot);
}이 부분. 뭐 없다.
만약 삭제할 노드가 루트노드일 때, 추가 처리를 위한 문장이다.
삭제 연산 후에도 포인터 변수는 루트노드를 가리켜야 하기에, 이 문장이 들어가는 것이다.
그리고 찐 짅ㅈ짜 마지막으로, 이진 탐색 트리에 저장된 데이터를 출력하기 위한 함수다. 별거 없다!!
void ShowIntData(int data) {
printf("%d ", data);
}
void BSTShowALL(BTreeNode * bst) {
InorderTraverse(bst, ShowIntData);
}진짜 끝이다. 길고 긴 과정이였다ㅏ..
여기까지