시작해보자.
13-2
충돌 문제의 해결
앞서 13-1에서 충돌에 대해선 그냥 단순히 "뭐다"하고 알아만 두라고 하고 넘겼었다.
충돌은 "피해야 하는" 문제방법이 아니고, "해결해야 하는 방법이다". 알아두자.
이렇게. 이번엔, 이 충돌을 해결하는 방법을 디테일하게 살펴보자.
선형 조사법, 이차 조사법
우선, 선형 조사법(Linear Probing). 만약 충돌이 발생하면, 그 옆자리가 비었는지 살핀 후, 만약 비어있다면 그 자리에 대신 저장한다.
만약 해쉬 함수가 f(x) = key % 7이고, 배열 arr[10]에 데이터를 저장한다고 생각하자.
만약 key가 8인 데이터가 있다면, idx 값이 1인 곳에 저장될거다.
그런데, 여기서 뒤이어 key가 1인 데이터를 저장한다면? 마찬가지로 idx 값이 1인 곳에 저장되어야 하지만, 이미 저장된 데이터가 존재하므로 충돌이 발생한다.
여기서 만약 선형 조사법을 써준다면, key(1)의 옆 빈자리인 2에 저장을 하게 된다.
그러면 k의 키에서 충돌이 발생하면,
f(k)+1 → f(k)+2 → f(k)+3.. 과 같이 선형 조사법이 전개가 된다.
하지만, 만약 많은 양의 데이터 (대충 만개라고 쳐보자)가 존재하면, 충돌의 횟수가 점차 증가하며 클러스터(cluster) 현상이 발생한다. 특정 영역에 데이터가 집중적으로 몰리는 현상이 발생한다는 얘기다.
만약 이 클러스터 현상이 빈번하게 발생한다면

저번 13-1에서 설명한 2번 그림처럼, 비효율적인 구조가 될 것이다.
그러면, 이런 문제는 어떻게 해결해줘야 할까.
이차 조사법(Quadratic Probing)이 있다.
앞서 선형 조사법의 f(k)+1 → f(k)+2 → f(k)+3.. 같은 구조에서, 뒤에 더해지는 +1 +2.. 를 조절하여 서로 간격을 넓혀준다.
f(k)+1제곱 → f(k)+2제곱 → f(k)+3제곱.. 이렇게.
그런데, 이것도 "선형 조사법보다는 나은" 방법이지, 최선의 대책은 아니다. 그러면, 어떻게 해야 최선의 대책을 세울 수 있을까?
이를 해결해줄 방법이 이중 해쉬 방식인데, 이를 설명하기 전에 앞서 slot의 상태에 DELETED가 있었던 이유를 설명하고 넘어가겠다.
아래 그림을 보자.
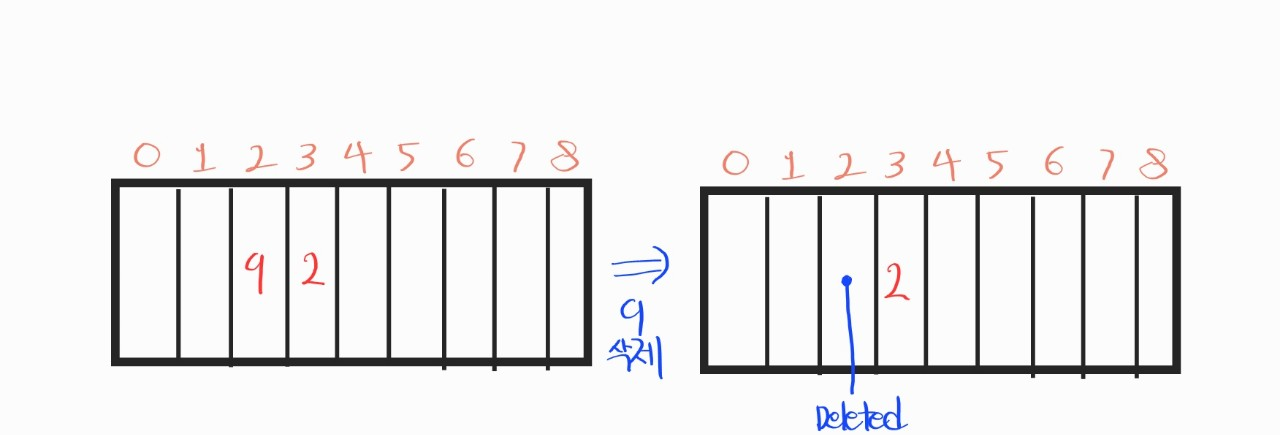
위의 분홍색 숫자들은 key를 나타낸다.
이 테이블의 해쉬 함수 f(x) = key % 6이고, key와 data가 각각 (2, 9) (8,2)인 데이터를 저장했다. 그러면 두개가 같은 해쉬값을 가져서, 충돌이 일어날 것이다. 이를 선형 조사법에 따라 저장한 결과물이 위의 앞그림이다.
여기서 key가 2인곳에 위치한 데이터를 삭제한다고 가정하면, 뒤에 있는 그림과 같이 될 것이다.
비어있는 공간은 empty 상태, 키가 3인 곳은 inuse상태, 키가 2인 곳은 deleted가 되었다.
여기서, 우리가 만약 키가 2인 데이터의 탐색을 진행한다고 가정하자. 그러면 현재 키가 3인 곳에 있는 데이터를 찾아야 할 것이다. 키가 2인곳에 있던 데이터는 지워졌고, 키가 3에있던 데이터도 원래는 키가 2였던 친구니까.
여기서 알아둬야할 새로운 사실은 아래와 같다.
-
슬롯의 상태에 deleted가 포함되어야 선형 / 이차조사법 같이 충돌 해결책을 사용 가능하다.
-
선형, 이차 조사법을 적용했으면, 탐색 과정에서도 이를 베이스로 충돌을 의심하는 탐색의 과정을 포함해야한다.
이중 해쉬(Double Hash)
앞서 언급한 이중 해쉬다.
앞서 이차 조사법도 아무리 거리를 늘린다해도 규칙성이 있고, 접근하는 위치가 항상 비슷하면 클러스터 현상이 발생할 가능성이 꽤 있었다. 하지만, 선형 조사법의 간격을 불균형하게 만들어준다면?
이러한 궁금증에 대한 답변이 이중 해쉬 방법이다.
두개의 해쉬함수를 사용하기에, 이중 해쉬라고 한다.
여기서 두개의 해쉬함수는 각각
1차 HASH : 키를 근거로 저장위치를 결정
2차 HASH : 충돌 발생 시, 몇 칸 뒤를 결장할지
를 의미한다.
1차는 그냥 앞서 언급했던 해쉬함수들과 똑같은 기능인데 (ex, f(x) = key % 7). 2차가 조금 다르다.
예시와 함꼐 설명하겠다.
만약 어떤 테이블이 있다고 치고, 1차 해쉬함수는 아래와 같이 지정했다.
hashone(k) = k % 15;
그러면, 아래 식을 근거로 2차 해쉬 함수를 결정한다.
hashtwo(k) = 1 + (k % c);
? 갑자기 뭔데요 저건
사실 내가 그렇게 당황했다. 한번 디테일하게 들어가보자.
hashone 에 % 15 있는걸로 비추어 보아, 배열의 길이는 15라고 예상할 수 있다. 이 때 hashtwo의 c는 15보다 적은 소수 중 하나로 결정한다. 2, 3, 5, 7, 11, 13 중 마음에 드는걸 고르면 된다.
hashtwo가 여러모로 의문인데, 왜그러는걸까.
먼저, 1을 더해주는 이유. 2차 해쉬 값이 0이 되는 것을 막기 위해서. 충돌 발생 이후, 다른 자리를 살피는데 해쉬값이 0이 되어버리면 곤란하지 않은가.
그 다음, c를 15보다 작은 소수로 고르는 이유는?
가급적 2차 해쉬 값이 1차 해쉬 값을 안 넘어서게 하려고. 만약 1차 해쉬값의 최대값이 14라고 치자. (15면 배열 길이가 16이겠지) 근데 2차 해쉬의 최대값이 32다? 그러면 쓸모없이 빈 자리를 찾으려고 몇 바퀴나 돌아야 하겠는가.
마지막으로, 왜 굳이 "소수"인가?
통계가 그렇단다. 소수를 선택하면 클러스터 현상의 발생확률을 현저!히 낮춘단다.
마지막으로 예시 하나를 들면, 키가 18인 데이터를 저장하면
h2(18) → h2(18) + 5 x 1 → h2(18) + 5 x 2 ... 이렇게 2차 해쉬값만큼 건너뛰면서 빈 슬롯을 찾는다.
키가 다르면, 건너 뛰는 길이도 다를거다. 그래서, 클러스터 현상의 발생확률을 확 낮춘다.
체이닝(Chaining)
앞의 선형 / 이차 조사법과 이중해쉬와는 아예 결이 다른 해결방식이다.
앞선 유형은 "열린 어드레싱 방법", 이 방법은 "닫힌 어드레싱 방법"이다.
그냥 쉽게 말하면, 열린 어드레싱 방법은 "어디에 데이터 저장하든 찾기만 해.." 느낌이면, 닫힌 어드레싱은 "반드시 내 자리에 저장될거야..!!" 라는 느낌이다.
..? 충돌이 발생하는데, 자신의 자리를 들어가겠다고? 이게 되나?
가능하니까 존재한다. ㅋㅋ; 그림을 보면
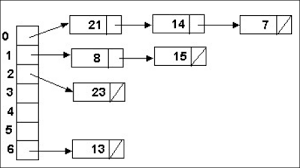
이런 식이다. 위의 그림은 연결리스트를 이용한 방식이고, 배열로 이용한 방식으로도 구현할 수 있다.
그림을 말로 표현하면, 슬롯을 생성하여 연결리스트의 모델로 연결해나가는 방식으로 충돌을 해결하는 것이다. 하나의 해쉬 값에 다수의 슬롯을 두며, 탐색을 한번 더 진행하는 불편함이 있지만, 해쉬함수를 잘 정의했다면 그렇게 많은 값이 한 곳에 저장되지는 않을 것이다.
그러면, 체이닝을 구현해보자. Linked List를 기반으로!
구현
우선, Slot 파일부터 새로이 구현하자.
사람들의 이름 / 주민번호와 같은 개인정보를 저장할 수 있는 프로그램을 만들거다.
자세한 파일들은 내 깃허브를 참고하자.
#ifndef __SLOT2_H__
#define __SLOT2_H__
#include "Person.h"
typedef int Key;
typedef Person * Value;
// Slot의 Status를 표시하기 위한 enum 선언이 사라졌다.
// 닫힌 어드레싱 방법의 경우에는 슬롯의 상태 정보를 표기할 이유가 없다.
// 어짜피 하나의 해쉬 값에 정보가 여러개 들어가니까.
typedef struct _slot
{
Key key;
Value val;
} Slot;
#endif주석에서 설명한 것 처럼, 13-1의 Slot 헤더파일과는 다르게 enum 선언이 사라졌다. 열린 어드레싱 방법처럼 DELETED를 확인하고 옆자리를 가거나 그런 수고를 여기선 할 필요가 없으니까..
그 다음, Table을 정의하는 헤더파일.
#ifndef __TABLE2_H__
#define __TABLE2_H__
#include "Slot2.h"
#include "DLinkedList.h"
#define MAX_TBL 100
typedef int (*HashFunc)(Key k); // 해쉬 함수
typedef struct _table {
List tbl[MAX_TBL]; // Slot형이 List형으로 바뀌었다.
HashFunc * hf;
} Table;
void TBLInit(Table * pt, HashFunc * f);
void TBLInsert(Table * pt, Key k, Value v);
Value TBLDelete(Table * pt, Key k);
Value TBLSearch(Table * pt, Key k);
#endif위에서 언급한 것 처럼, slot형을 list형으로 바꾸었다는 점. Ch.13-1의 예시와는 그게 바뀌었다.
그리고, 연결 리스트의 헤더파일에도 typedef int LData 를 typedef Slot LData로 바꾸어줘야 한다. 슬롯이 노드의 멤버가 되게 하기 위해서다. 혹시 의아할까봐, 그림도.

그 다음, Table 소스파일.
아마 필요한 설명은 다 주석에 있을 것이다.
#include <stdio.h>
#include <stdlib.h>
#include "Table2.h"
#include "DLinkedList.h"
void TBLInit(Table * pt, HashFunc * f) {
int i;
for (i=0 ; i<MAX_TBL ; i++) {
ListInit(&(pt->tbl[i]));
}
pt->hf = f;
}
void TBLInsert(Table * pt, Key k, Value v) {
int hv = pt->hf(k);
// hv에는 해쉬값을 저장한다. 즉, 최종적으로 Slot(k,v)가 저장될 idx값.
Slot ns = {k, v};
if (TBLSearch(pt, k) != NULL) { // 키 중복
printf("Key Duplication Error\n");
return;
} else { // 키 중복이 아니라면
LInsert(&(pt->tbl[hv]), ns); // Table의 해쉬값을 인덱스로 하는 위치에 ns 저장.
}
}
Value TBLDelete(Table * pt, Key k) {
int hv = pt->hf(k);
Slot cSlot;
if (LFirst(&pt->tbl[hv], &cSlot)) { // list의 첫 데이터
if (cSlot.key == k) { // 만약 지금 slot의 key(cSlot.key)가 내가 찾는 key(k)와 같다면
LRemove(&(pt->tbl[hv]));
return cSlot.val;
} else {
while(LNext(&(pt->tbl[hv]), &cSlot)) {
if (cSlot.key == k) { // 만약 지금 slot의 key(cSlot.key)가 내가 찾는 key(k)와 같다면
LRemove(&(pt->tbl[hv]));
return cSlot.val;
}
}
}
}
return NULL;
}
Value TBLSearch(Table * pt, Key k) {
int hv = pt->hf(k);
Slot cSlot;
if (LFirst(&pt->tbl[hv], &cSlot)) { // list의 첫 데이터
if (cSlot.key == k) { // 만약 지금 slot의 key(cSlot.key)가 내가 찾는 key(k)와 같다면
return cSlot.val;
} else {
while(LNext(&(pt->tbl[hv]), &cSlot)) {
if (cSlot.key == k) {
return cSlot.val;
}
}
}
}
return NULL;
}이렇게, 테이블에 대한 구현은 끝이 난다. 메인 함수는 위의 깃허브를 확인하자.
그리고, 이게 끝이라고 방심하지 않고, 명심해야할게있다.
만약 우리가 Value가 포인터 형이 아니였다면, 만약 int형이였다면? return NULL 이 탐색 실패를 의미할 수 있을까? (in TBLSearch, TBLDelete)
아니다. int형으로 NULL을 반환했으면 0을 반환했으므로 뭔가 의미있는 인덱스 값을 전달한 것 처럼 될수도 있다.
만약 "Value가 포인터 형이 아니다"라는 상황에서는, 이 return을 "FALSE"로 하도록 하자.
여기까지