2021년의 마지막 날이다.

어째 어째 시간을 날려먹다보니, 벌써 한해가 가네. 내년부터 복학할 생각을 하니 쪼끔 머리가 띵하다. 열심히 살자.

-- 1월 3일 추가 --
211231에 썼는데, 왜인지 모르겠지만 업로드가 안되어있어서, 1월 3일에 업로드한다.

Ch.14 Graph

14-1

이번 챕터에선 그래프(Graph)에 대해 다룬다.

Graph

그래프?

흔히 우리가 생각하는 그래프를 떠올려보면, 직교좌표계의 y=x 함수같은 그래프를 떠올린다. 하지만, 여기서는 그런 그래프와는 좀 많이 다르다는 것을 먼저 인지하고 가자.

네X버 지도, X글 맵같은 어플을 켜면 버스 / 지하철의 노선도를 확인하고, 출발지와 목적지를 정해서 최단거리로 어떻게 이동하는지 알려주는데, 이런 프로그램을 구현하는데에 사용되는 것이 그래프 알고리즘이다.

출처

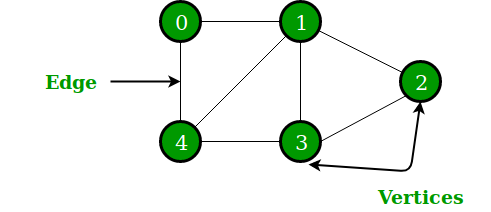
이렇게 생겼다. 여기서 Vertices(복수라 Vertices지, 원래는 Vertex)는 "정점", Edge는 "간선" 이라고 한다.

만약 내가 광화문역에서 왕십리역까지 갈거라고 치면, 광화문역과 왕십리역은 각각 정점이 되고, 가는 그 동선은 간선이 될거다. 이렇게 이해하면 편하겠다.

그래프의 종류

그래프의 종류엔 여러개가 있다.

일단, 가장 큰 갈래로 나누면 무방향 그래프(Undirected Graph), 방향 그래프(Directed Graph / Digraph)로 나뉜다.]

출처

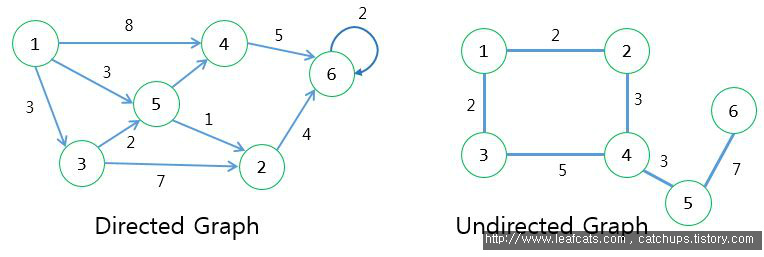
왼쪽 그림을 보면, 간선에 방향이 표시되어있다. 그러면 방향그래프. 반면, 오른쪽은 방향 없이 그냥 간선만 죽죽 그어져있다. 저건 무방향그래프.

그리고 간선 위에 숫자가 표시되어 있는데, 저건 가중치(Weight) 라고 한다. "정점 A에서 정점 B까지 가는데 걸리는 시간", "정점A와 정점B 사이의 거리" 와 같은 정보들을 개발자가 원하는대로 지정할 수 있다. 이런 가중치가 들어간 그래프를 보고 "가중치 그래프" 라고도 한다.

물론, 꼭 위의 그림처럼 가중치가 들어가야"만" 하는 것은 아니다. 없어도 된다.

만약 모든 정점들에 서로 오가는 간선이 있다면, 완전 그래프라고 한다.

출처

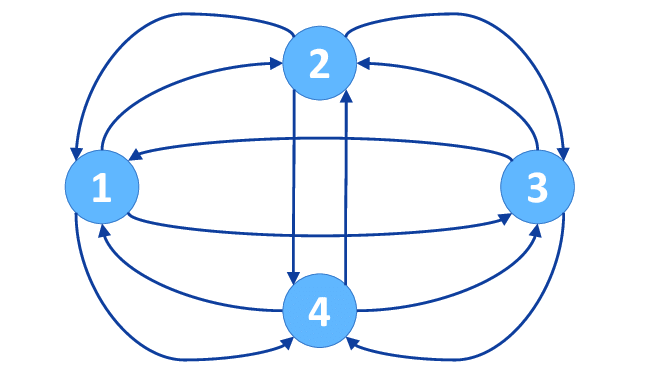
이렇게.

그리고, 우리가 Tree를 학습할 때 SubTree란 개념이 있었다. 여기도 마찬가지로 부분 그래프(Sub Graph)라는 개념이 있다.

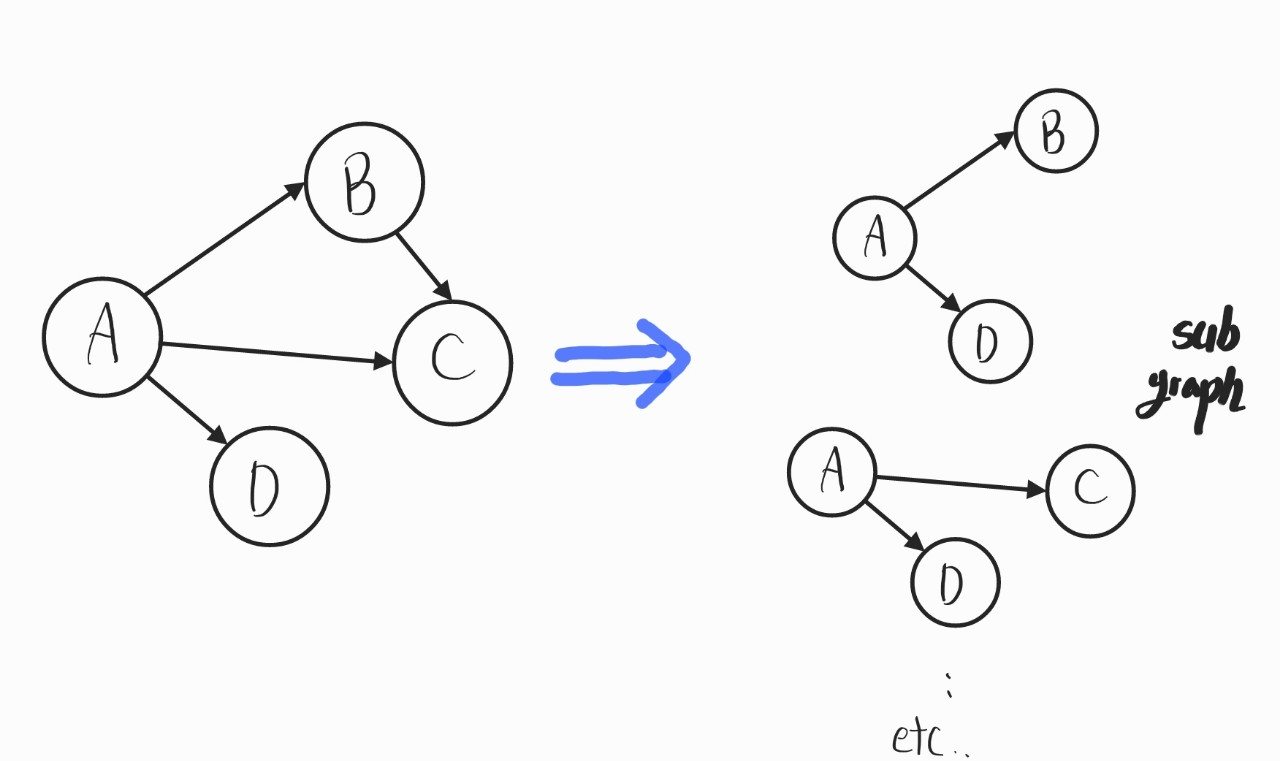
왼쪽의 Main Graph에서 몇몇 부분만 떼어내면 그걸 Sub Graph라고 한다.

그래프의 집합

그래프는 구성원인 "정점"과 "간선"의 집합이라고 볼 수 있다.

그래서, 집합으로도 표현이 가능하다는 점.

무방향 그래프 하나, 방향 그래프 하나로 총 두개의 예시를 들겠다.

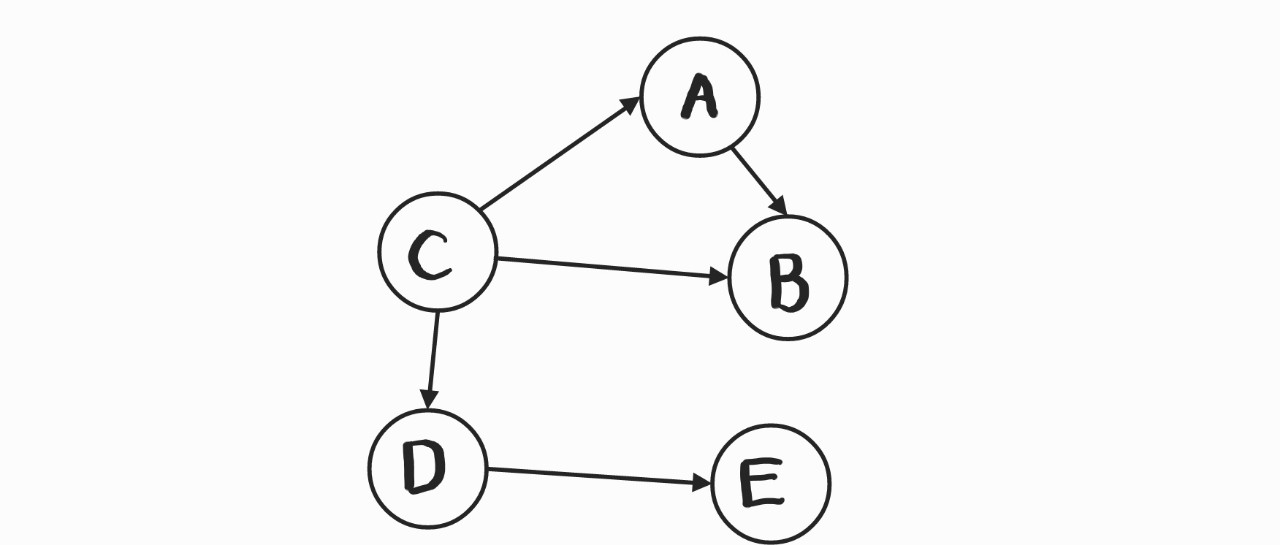
우선, 방향 그래프. 정점은 A~E 다섯개. 그래서 정점 표현은

			V(G) = {A, B, C, D, E}

이다. 간선은 "방향"그래프 이므로 <>로 표현하는데, <from, to> 로 표현하면 된다. from에서 to로 향한다고 생각하자.

		E(G) = {<A,B>, <C,A>, <C,B>, <C,D>, <D,E>}

간선 표현은 위와 같다.

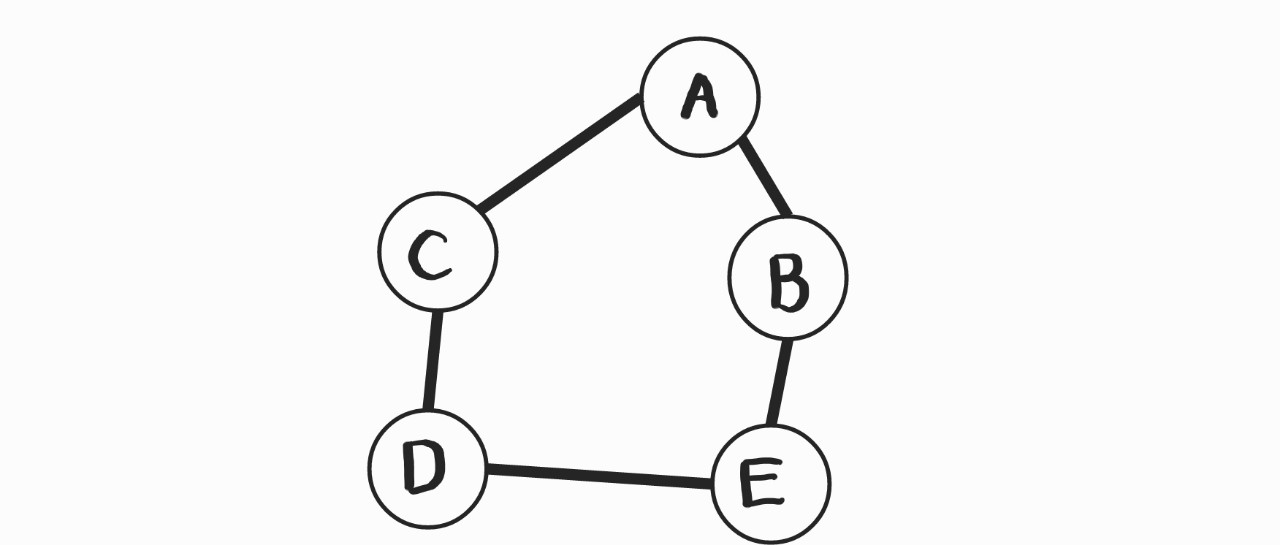
이 그래프도 위와 정점 집합의 표현은 같으므로 생략하겠다.
단, 간선 집합의 표현이 좀 다른데, "무방향" 그래프라 (from, to)로 표현한다.

		E(G) = {(A,B), (B,C), (C,D), (D,E), (A, E)}

이와 같다.

구현 시작! ADT set

우리는 막 디테일하게 그래프의 이런 저런 기능을 다 구현할 수 있는 코드를 만들진 않을것이다. 하지만, 우리는 이 자료구조를 통해 탐색을 할 수 있는 응용프로그램을 만드는게 목적이다. 어떻게 보면, 그래프를 구성하는 것 보다 이 구성된 그래프를 제대로 써먹을 줄 아는게 더 중요하다고 할 수 있다.

그래서, "꼭" 필요한 기능만을 ADT에 넣도록 한다!

void GraphInit(ALGraph *pg, int nv);
// 그래프의 초기화. nv를 통해 정점의 개수를 전달받는다.

void GraphDestroy(ALGraph *pg);
// 그래프의 Resource 해제. 초기화 과정에서 할당한 리소스를 반환함. 쉽게 말해 동적 할당에서 free함수의 역할을 생각하자.

void AddEdge(ALGraph *ph, int fromV, int toV);
// 간선 추가.

void ShowGraphEdgeInfo(ALGraph *pg);
// 간선의 정보를 출력한다.

우리가 정의할 ADT는 위의 네개다. 실제 응용프로그램에 써먹을 때도 이정도면 된다고 한다.

근데, 이렇게 되면, 각 정점에 고유성을 부여, 즉 이름을 부여할 수 없지 않나..?

~~라고 할뻔 했지만, 이후에 이 ADT와 함께 헤더파일에 enum 열거형 상수를 하나 선언할 것이다.

이후에 헤더파일에 설명을 달아줄테니, 그때 잘~ 보자.

어떻게 구현해야할까

그래프를 구현하는 방법도 앞서 다른친구들과 큰 차이가 없다. 두개로 나뉘는데, 배열기반, 리스트기반. 두개다.

배열을 기반으로 하는 방법을 인접 행렬(adjacent matrix)기반 그래프, 연결 리스트를 기반으로 하는 방법을 인접 리스트(adjacent list) 기반 그래프 라고 한다.

우선, 인접 행렬 그래프.

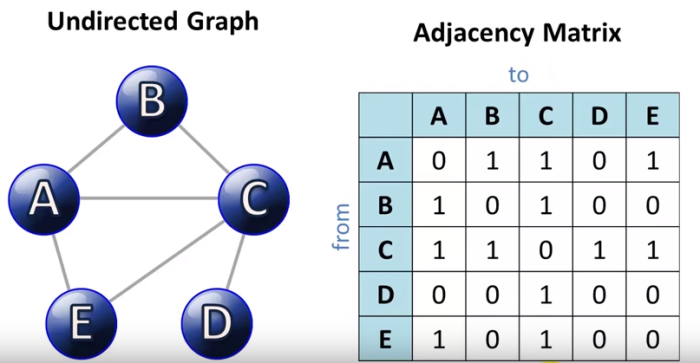
여기선 정방 행렬(가로/세로 길이가 같은 행렬)을 사용한다. 그러면 4x4, 6x6의 표를 생각해주면 편한데, 그러면 2차원 배열을 써야하지 않을까.

출처

정점의 개수가 n개이면 nxn 2차원 배열을 선언해준다. 위의 그림의 경우
엔 정점이 5개이므로 5x5 2차원 배열을 선언했다. 여기서 두 정점이 연결되어 있을시 1, 연결되어있지 않을시 0으로 표시한다. 위의 그림에서 한 점만 예시로 들면, A열 B행을 보면, A-B가 연결되어 있어서 1로 표시되어 있다.

그리고 잘 보면, arr[m][n]인 부분이 1이면 arr[n][m]인 부분도 1이다. 그리고 대각선은 다 0. 이 행렬은 대각선을 기준으로 대칭 구조를 이루게 된다.

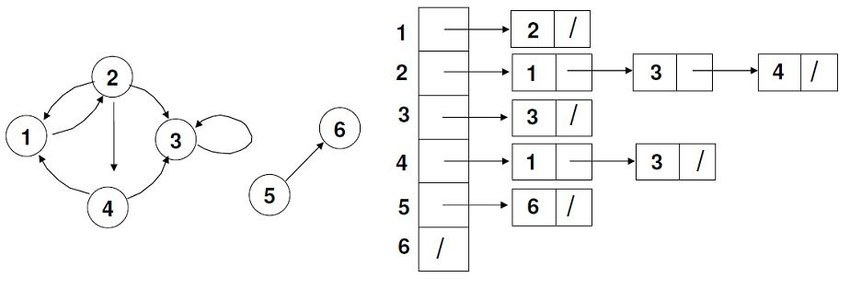
이번엔 인접 리스트 그래프.

출처

이 예시의 경우엔 1과 2가 서로를 가리키고 있으므로 1->2, 2->1이 다 존재한다는 걸 알 수 있다. 나머지는 한방향이라 하나씩만 담겨있는걸 확인할 수 있다.

만약 무방향 그래프의 경우라면 서로 가리키는것과 별개로 1과 2사이가 이어져있다는걸 나타내기 위해 위처럼 1->2, 2->1을 다 표기해줘야 한다.

14-2

본격적인 구현

이 책에서는 인접 리스트 기반의 그래프 구현을 보여주므로, 나도 이에 따르겠다. 그리고 그 중에서도 "무방향 그래프"를 구현하겠다.

"리스트" 기반이니, 리스트에 필요한 헤더파일이 필요 하므로 Ch.04의 "DLinkedList.h"를 좀 갖다쓰자!

우선, 헤더파일을 보자.

#ifndef __AL_GRAPH__ // 무방향 그래프의 경우
#define __AL_GRAPH__

#include "DLinkedList.h" // 연결 리스트 가져다 씀

enum {A, B, C, D, E, F, G, H, I, J}; // 정점들의 이름을 enum을 통해 상수화

typedef struct _ual {
    int numV; // 정점 개수
    int numE; // 간선 개수
    List *adjList; // 간선의 정보
} ALGraph;

void GraphInit(ALGraph *pg, int nv);
// 그래프의 초기화. nv를 통해 정점의 개수를 전달받는다.

void GraphDestroy(ALGraph *pg);
// 그래프의 Resource 해제. 초기화 과정에서 할당한 리소스를 반환함. 
// 쉽게 말해 동적 할당에서 free함수의 역할을 생각하자.

void AddEdge(ALGraph *ph, int fromV, int toV);
// 간선 추가.

void ShowGraphEdgeInfo(ALGraph *pg);
// 간선의 정보를 출력한다.

#endif

딱히 여기서 설명할게 크게 없다. 해봐야 그래프를 나타내는 구조체, 열거형 상수 enum정도?

구조체는 numV, numE로 정점과 간선의 개수를 나타낸다. 그리고 adjList는 간선의 정보를 담는데, 인접 리스트 그래프의 예시에서 오른쪽에 있는 연결리스트 그림을 보면 된다.

enum의 경우엔 만약 필요한 정점의 수가 10개를 넘는다면 이름을 더 추가하면 된다. 응용프로그램을 만드는 거라면 이름을 바궈주면 된다.

이제 이 헤더파일을 밑받침해줄 소스파일이 필요하지 않을까. 설명은 주석으로 첨부하겠다.

#include <stdio.h>
#include <stdlib.h>
#include "ALGraph.h"
#include "DLinkedList.h"

void GraphInit(ALGraph *pg, int nv) {
    // 정점의 수에 해당하는 길이의 List 배열 생성
    pg->adjList = (List *) malloc(sizeof(List)*nv);
    // 여기에, 간선 정보가 저장될것임. 누가 누구랑 연결되어있나. 그런거.
    // *nv인 이유는 정점의 개수만큼 표시해줘야하니깐.
    
    pg->numV = nv; // 정점의 수를 인자 nv로 결정
    pg->numE = 0; // 아직 만들어진 선은 없어

    for (int i=0 ; i<nv ; i++) {
        ListInit(&(pg->adjList[i]));
    }
}

void GraphDestroy(ALGraph *pg) { 
    if (pg->adjList != NULL) {
        free(pg->adjList);
    }
}

void AddEdge(ALGraph *ph, int fromV, int toV) {
    
    // fromV의 연결 리스트에 toV의 정보를 추가.
    // 만약 fromV가 B, toV가 D라면,
    // adjList[B]에 D가 연결되어있다는걸 알리기 위해 D를 LInsert 해주는 것이다.
    
    LInsert(&(pg->adjList[fromV]), toV);

    LInsert(&(pg->adjList[toV]), fromV);
    pg->numE += 1;
}

void ShowGraphEdgeInfo(ALGraph *pg) {
    
    int vx;

    for(int i=0; i<pg->numV ; i++) {
        printf("Vertex connected to %c", i + 65);
        // 문자의 출력을 위해 65 더함

        if(LFirst(&(pg->adjList[i]), &vx)) {
            printf("%c ", vx + 65);
        
            while(LNext(&(pg->adjList[i]), &vx)) {
                printf("%c ", vx+65);
            }
        }

        printf("\n");
    }
}

여기까지.