[Aiffel] 아이펠 31일차 개념 정리 및 회고
ARARIMAAugmented Dickey-Fuller TestMAiinterpolate()p-valuerolling meanrolling stdstationary공분산국비교육분산상관계수시계열아이펠이동평균이동표준편차파이썬회귀분석
Aiffel / 아이펠 양재 2기
목록 보기
32/74
1. 딥러닝 개념 정리
1) 시계열(Time series) 예측
- 시계열의 의미
순서대로 발생한 데이터의 수열ex)날짜-가격의 형태의 데이터가 있다면 날짜가 인덱스 역할을 함
미래 예측의 전제
- 과거의 데이터에 일정 패턴이 발견됨
- 해당 패턴이 미래에도 동일하게 반복될 것
⇒ Stationary data에 대해서만 미래 예측이 가능
- stationary = 시계열 데이터가 가지는 통계적 특성의 변화가 없음
- Stationarity
-
조건: 다음 세 가지가 일정해야함 (시간에 따라서 변동한다든가 하면 안됨)
- mean
- variance: 차이값의 제곱의 평균
- covariance(공분산): 확률변수 x, y의 관계를 나타냄
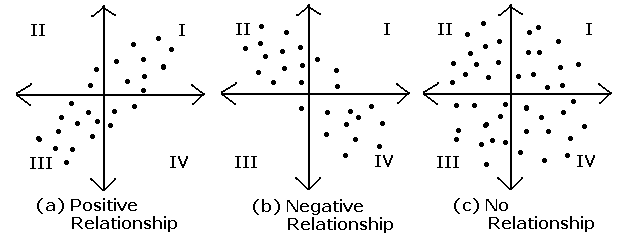
- 출처
- 두 변수가 독립적인 경우 공분산은 0이지만 역은 성립하지 않음.
- x의 편차와 y의 편차를 곱해 평균을 낸 값
상관계수
확률변수의 단위 크기에 영향을 받는 공분산의 특징을 보완하기 위해 도입한 개념
확률변수의 절대적인 크기의 영향을 벗어나도록 단위화 시키는 과정이라고 생각하면 됨.
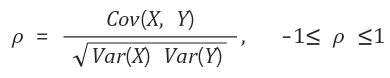
- 성질
- 1 이하이다.
- x, y가 독립이면 상관계수는 0이다.
- x, y가 선형적 관계라면 상관계수는 양의 선형관계일 경우 1, 음의 선형 관계일 경우 -1이다.
-
autocovariance & autocorrelation
- autocovariance: 완전히 일치하는 자기 자신이 아니라 일정 간격만큼 이동한 자기 자신과의 공분산임
2) 시계열 데이터 사례분석
- pandas로 데이터 불러오기
df = pd.read_csv(dataset_filepath, index_col = 'Date', parse_dates=True)
df.head()
df.index| Temp | |
|---|---|
| Date | |
| 1981-01-01 | 20.7 |
| 1981-01-02 | 17.9 |
| 1981-01-03 | 18.8 |
| 1981-01-04 | 14.6 |
| 1981-01-05 | 15.8 |
- parse_dates: datetime format으로 읽어올 수 있게 해준다. 지정하지 않을 경우 object format으로 읽어온다.
- df.index: index의 정보를 확인할 수 있다. 마지막에 dtype을 출력해준다. 여기서 확인해보면 parse_dates=True가 없을 경우엔 object, 있을 경우엔 datetime64[ns]로 출력된다.
- 안정성의 정성적 분석
- 시각화를 통해 확인함
- 결측치가 있는 경우: 오류의 원인, 분석 결과에도 영향
- 결측치가 있는 데이터를 모두 삭제
- 결측치 양옆의 값을 이용해 적절히 interpolate(보간)하여 대입
# 결측치가 있다면 이를 보간합니다. 보간 기준은 time을 선택합니다. ts1=ts1.interpolate(method='time')- 판다스에서는 보간 방식으로
df.interpolate(method='')를 사용함
- 구간 통계치
- 구간의 평균: rolling mean, 이동평균
- 표준편차: rolling std, 이동표준편차
3) Augmented Dickey-Fuller Test
- 통계적으로 stationary 여부를 확인하는 방법
증명
1. 귀무가설(Null hypothesis): 주어진 시계열 데이터는 안정적이지 않다.
2. 통계적 가설 검정과정을 통해 귀무가설이 기각된다.
3. 2를 통해 대립가설(alternative hypothesis, 시계열 데이터는 안정적이다.)을 채택한다.
- p-value: 귀무가설이 참이라고 가정할 시, 얻은 결과보다 극단적인 결과가 실제로 나타날 확률
- p 값이 낮을 경우 해당 표본 통계량은 우연히 나타나기 어려운 케이스이기 때문에 귀무가설 대신 대립가설을 채택함
| ADF 검정 | |
|---|---|
| 방식 | 단위근(x=1, y=1인 해) 검정 방식 |
| 귀무가설 | 자료에 단위근이 존재한다. |
| 대립가설 | 단위근이 존재하지 않는다. 따라서 시계열 자료가 정상성을 만족한다. |
| 원리 | 검정통계량이 critical value보다 작거나 p-value가 설정한 유의수준 값보다 작으면 정상적인 시계열 데이터 |
4) 시계열 데이터 가공
- 방법
- 이전과 비교해 안정적인 특성을 가지도록 기존의 시계열 데이터를 가공/변형(정상적인 분석을 통함)
- 시계열 분해(Time series decomposition) 기법을 적용
1. 가공
- 로그함수로 변환
- 시간이 지남에 따라 분산이 증가할 때 사용 가능
- 추세 상쇄하기
- 추세: 시간의 추이에 다라 나타나는 평균값의 변화
- rolling mean(moving average)를 구해서 ts_log에서 빼줌.
- moving average를 고려할 시 window가 중요. 바뀌면 값도 p-value도 바뀔 가능성이 큼
- 차분(Differencing)
- Seasonality: 추세에는 잡히지 않지만 시계열 데이터 안에 포함된 주기적 변화
- 차분: 본래의 시계열에서 시계열을 한 스탭 앞으로 옮긴 시계열 데이터를 빼준다.(이번 스탭에서 발생한 변화량을 의미함)
- 여러 번 시도 가능
2. 시계열 분해
statsmodels 라이브러리 안의 seasonal_decompose 메소드를 이용해 시계열 내에 존재하는 trend, seasonality를 직접 분리함.
Original = Trend+Seasonality+Residual
- residual: trend, seasonality를 original에서 분리하고 남은 값
5) ARIMA(Autoregressive Integrated Moving Average)
1. 모델의 정의
- AR(Autoregressive)
- Yt가 q개의 데이터의 가중합으로 수렴한다고 보는 모델
- 과거 값들에 대한 회귀를 기반으로 미래의 값을 예측
- 시계열의 residual에 해당하는 부분을 모델링함
- ex) 주식 값은 항상 일정한 균형 수준을 유지할 것이다.
- MA(이동평균, Moving average)
- Yt가 q개의 예측오차값의 가중합으로 수렴한다고 보는 모델
- 시계열의 trend에 해당하는 부분을 모델링함
- ex) 주식 값이 최근의 증감 패턴을 지속할 것이라고 보는 관점
- I(차분 누적, Integration)
- Yt가 이전의 테이터와 d차 차분의 누적합이라고 보는 모델
- 시계열 데이터의 seasonality에 해당하는 부분을 모델링
2. 모델의 모수
- p: 자기 회귀 모형(AR)의 시차
- d: 차분 누적(I) 횟수
- q: 이동평균 모형(MA)의 시차
- 일반적으로
p + q < 2,p * q = 0인 값을 사용 - p와 q 둘 중 하나는 0, AR이나 MA 중 하나의 경향만 가지는 경우가 많기 때문
- 방법: ACF(Autocorrelation Function), PACF(Partial Autocorrelation Function)
- d는 d차 차분을 계산해서 결정
2. 회고
말로만 듣던 시계열을 처음 접해봤는데 지금까지 거쳐간 ex 노드 중에 제일 재밌었다. 무엇보다 결과가 빨리 나와서 좋았다.. 이해하고 넘어간 줄 알았는데 정작 다른 회사의 주식 값을 예측할 땐 이게 뭐지 싶어서 다시 앞으로 가서 확인하고 하는 과정이 많았다. 이런 걸 보면 내용을 확실히 이해한 것은 분명 아닌 듯 싶다. 그럼에도 함수로 구성하고 예측하는 과정이 재밌어서 더 공부할 수 있다면 이쪽에 관심을 가지고 하지 않을까 생각한다.
