[Aiffel] 아이펠 32일차 개념 정리 및 회고
Batch NormalizationL1 RegularizationL2 regularizationLp normNormalizationRegularizationdropout국비교육딥러닝아이펠요약파이썬
Aiffel / 아이펠 양재 2기
목록 보기
33/74
1. 딥러닝 개념
1) Regularization & Normalization
| Regularization | Normalization | |
|---|---|---|
| 목적 | overfitting 해결 | 데이터의 형태를 트레이닝에 적합하도록 전처리하는 과정 |
| 방법 | 1. L1 regularization 2. L2 regularization 3. Batch normalization | z-score, minmax scaler |
2) L1 regularization
- 정의
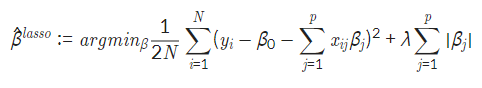
- 마지막에 더하는 부분이 없은면 linear regression과 동일함
- Lp norm이 1일 때를 나타내는 것
- Lp norm 공식
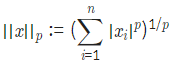
- Lp norm 공식
- 특징
- X가 1차원 값인 선형회귀분석에서는 효과가 없음, 2차원 이상일 때 사용해야함
- Linear regression vs L1 regularization
- coefficient를 계산했을 때 차이가 크게 남: 어떤 column이 더 영향을 미치는지 쉽게 알 수 있음
- 다른 문제에서도 큰 차이가 나지 않으면 0이 나온 변수를 제외하고 나머지만 이용해도 결과 예측은 충분히 가능함.
- coefficient를 계산했을 때 차이가 크게 남: 어떤 column이 더 영향을 미치는지 쉽게 알 수 있음
3) L2 regularization
- 정의
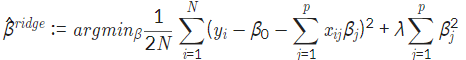
- 마지막 더하는 부분은 Lp norm이 2일 때를 나타냄
- vs L1 regularization
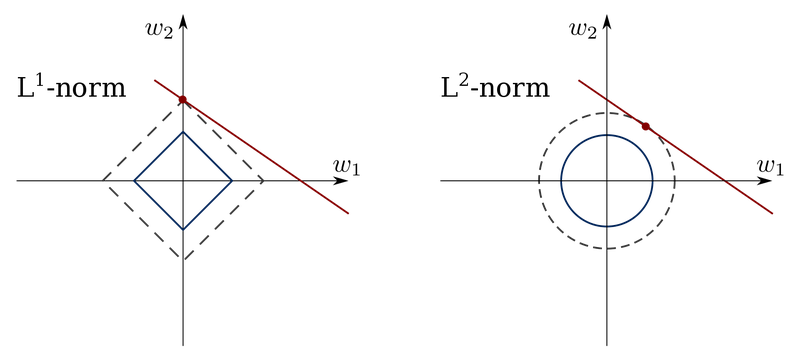
| L1 | L2 | |
|---|---|---|
| 형태 | 마름모 | 원 |
| β | 0이 될 때 있음 | 0으로 수렴 |
| 특징 | 가중치가 적은 벡터에 해당하는 계수를 0으로 보내 차원 축소와 비슷한 역할을 함 | 제곱을 사용하기 때문에 결과에 미치는 영향이 큰 값은 더 크게, 반대의 경우는 더 작게 보내 L1에 비해 수렴이 빠름 |
4) Lp norm
-
norm 이란?
벡터, 함수, 행렬에 대해 크기를 구하는 것 -
matrix norm
행렬의 norm은 벡터와는 다름. 주로 p=1, p=∞인 경우를 알면 됨
A가 m*n 행렬일 때
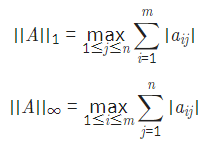
위의 경우는 여러 개의 열 중 열의 합이 가장 큰 값이 출력
밑의 경우는 여러 개의 행 중 행의 합이 가장 큰 값이 출력됨
5) Dropout
- 등장이전 상황
- Fully connected architecture: 모든 뉴런이 연결됨 ⇒ 계산량 많음
- Dropout
- regularization의 방법 중 하나
- 확률이 지나치게 클 경우: 제대로 전달되지 않아 학습이 잘 안됨
- 확률이 지나치게 낮은 경우: fully connected layer와 차이가 없음
- fc layer가 overfitting되는 경우 주로 사용
6) Batch normalization
gradient vanishing, explode 문제를 해결하기 위한 방법

- 3단계에서 분모에 ϵ가 추가됨으로써 normalize과정에서 vanishing과 explode를 막을 수 있음.
- ϵ가 없으면 기존의 z-score로 normalization하는 것과 같음
- batch normalization으로 인해 입력값이 정규화되어 좀 더 고른 분포를 가지고, ϵ 부분이 통해 안정적인 학습을 가능하게 함
2. 지금까지 배운 내용 정리
1) 머신러닝 모델 분류
1. 지도 학습
- 분류
- 회귀: 잔차가 평균으로 회귀하는 것
| 용어 | 관련 개념 | 설명 |
|---|---|---|
| 활성함수 | sigmoid, sofmax, 회귀분석 | 인공신경망에서 입력을 변환하는 함수 |
| sigmoid | 로지스틱 회귀분석 Neural Network의 binary classification | hidden layer에서 계산된 값의 결과를 0-1로 바꿔주는 단계에서 사용되는 함수 sigmoid 함수를 사용하는 이유 |
| softmax | 다항 로지스틱 회귀 | 로지스틱 함수의 다차원 일반화 |
| 오차역전파법(backpropagation) | 손실함수, 경사하강법, 최적화 | 가중치의 매개변수의 기울기를 효과적으로 구하는 방법 |
| 손실함수 | 경사하강법, 회귀: [MAE, MSE, RMSE], 분류: [binary cross entropy, categorial cross entropy] | 머신러닝 모델의 예측값이 실제 값과 얼마나 유사한지 판단하는 기준, loss를 줄이는 방향으로 학습 |
| 경사하강법 | 손실함수, 최적화(opimization), 배치 gd, 확률적 gd, 미니배치 gd, 모멘텀, 아담 | 손실함수의 결과값이 최소값이 되는 최적인 모델의 파라미터를 찾는 과정 |
| regularization | lasso(L1), ridge(L2) | 과적합을 방지하기 위한 방법 중 하나. train set의 정답을 맞히지 못하도록 오버피팅을 방해해 결과적으로 validation loss 혹은 test loss를 줄이고자 함. 참고로 KNN에서 L1 distance, L2 distance 중 하나를 고르는데 이 개념과 헷갈리지 말자. |
| dropout | regularization | 뉴런 중 확률적으로 몇 가지만 선택해서 정보를 전달하게 하는 과정 |
| normalization | 경사하강법 | gradient vanishing, explode를 해결하기 위한 방법, Conv2D 같은 레이어를 생성한 뒤 사용. 과정 중엔 폐렴 분류에 사용함 |
2. 비지도 학습
- clustering
- 차원축소
- 참고
3. 회고
오늘 노드를 끝내고 나니까 갑자기 개념들이 뒤섞이면서 어떤 함수를 언제 쓰는지가 헷갈려서 내용을 정리했다. pooling 같이 안쓴 것도 있긴 한데 그건 비교적 특정한 모델에서 쓰이는 개념이라 덜 헷갈리는 것 같아 일단 넘어갔다. 그래도 위에 나오지 않은 개념에 대해서 완벽하게 설명할 수 있다는 건 아니다. 어쨌든 한 번 정리를 하고 나니 상반기 목표에 가까워진 기분이다.
