Triplanar란 오브젝트의 X, Y, Z축을 바라보고 있는 영역을 관리할 수 있게끔 해주는 기술로 이해를 했다. 유튜브 자료를 찾아보니 보통 (1)오브젝트 위에 모래나 눈, 풀 등이 쌓여있는 듯한 연출, (2)실시간으로 바뀌는 지형(UV맵을 따로 펴주기 어려움)쉐이더 등에 사용되는 것 같다.
(1)은 유니티 코리아 유튜브의 해당 영상을 참고하면 좋을 듯 https://www.youtube.com/watch?v=Zz8-5iYQucE&ab_channel=UnityKorea
내가 이 트라이플래너 쉐이더를 만들어야 했던 상황은 다음과 같았다.
- 모델링에 윗면과 아랫면(Y방향)에만 다른 텍스쳐가 들어가야 했다.
- 텍스쳐 크기를 최대 1024px로 맞춰야 했는데, 사용해야 하는 텍스쳐 사이즈에 비해 모델의 사이즈가 커 텍스쳐를 따로 제작해도, 화질 저하가 일어날 수 있다.
- 디테일 맵으로 넣어서 타일링으로 조절해줄 수 있지만 타일처럼 반복되는 형태의 텍스쳐가 들어가야 했다. 큰 텍스쳐 한 장을 만들거나, UV를 펴서 딱 맞게 타일을 관리해주기 어려운 상황이었다.
아무튼 위 조건 때문에 쉐이더를 만들었어야 했었다.
이 글에서는 Triplanar 구조를 파악하는 것을 목표로 작성할 예정이다.
원리 이해하기
XYZ 각 축을 바라보는 방향에 따른 텍스쳐를 관리할 수 있다.
=> 이 말을 풀면, 각 축을 향하는 방향(노말)을 구하고, 그 값에 사용할 텍스쳐를 마스킹을 해주면 된다는 뜻이다. 바로 고고
1. 면이 바라보는 방향 구하기
월드 기준의 기즈모를 보면 X축은 빨간색, Y축은 연두, Z 축은 파란색이다.
R, G, B에 대입해서 생각해보면 바로 그려진다.
X = (1, 0, 0)
Y = (0, 1, 0)
Z = (0, 0, 1)
유니티에서 보여지는 XYZ축, 월드 축 색상 자체를 받아와서 렌더링 해주면 다음 이미지처럼 된다.월드 기준의 바라보는 방향(노말)의 구조를 파악했으니, 이를 직접 색상으로 표현해보자.
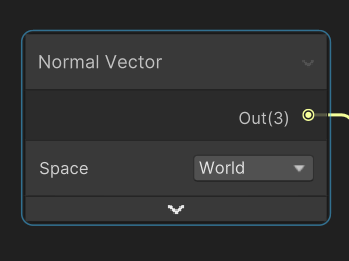
Normal Vector 노드를 생성하고, Space를 World로 설정한다. 이 Out 값을 마스터노드의 Base Color에 넣으면 아래 이미지처럼 된다.

이 때, Absolute해주지 않으면 다른 면이 -방향이기 때문에 검정 색상이 나온다.
뒤를 바라보는 방향에도 텍스쳐를 넣어주고 싶다면 Absolute 노드를 추가해주자.
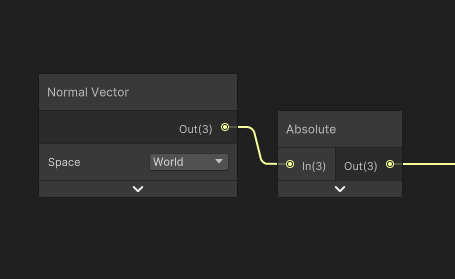
이렇게 Absolute노드를 추가해주면 뒷면도 정상적으로 색깔이 나온다.2. 마스킹을 해보자
향하는 방향을 구했다. X를 향하는 색상은 R, Y은 G, Z은 B 였다.
마스킹을 해주기 위해 split 노드를 추가해주자
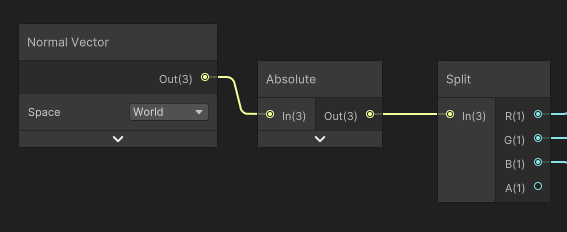
이렇게 split 해주었으면, 각 컬러 영역에 넣어줄 텍스쳐와 multiply 해주고, 마지막으로 add 해주면 끝난다. 오예!
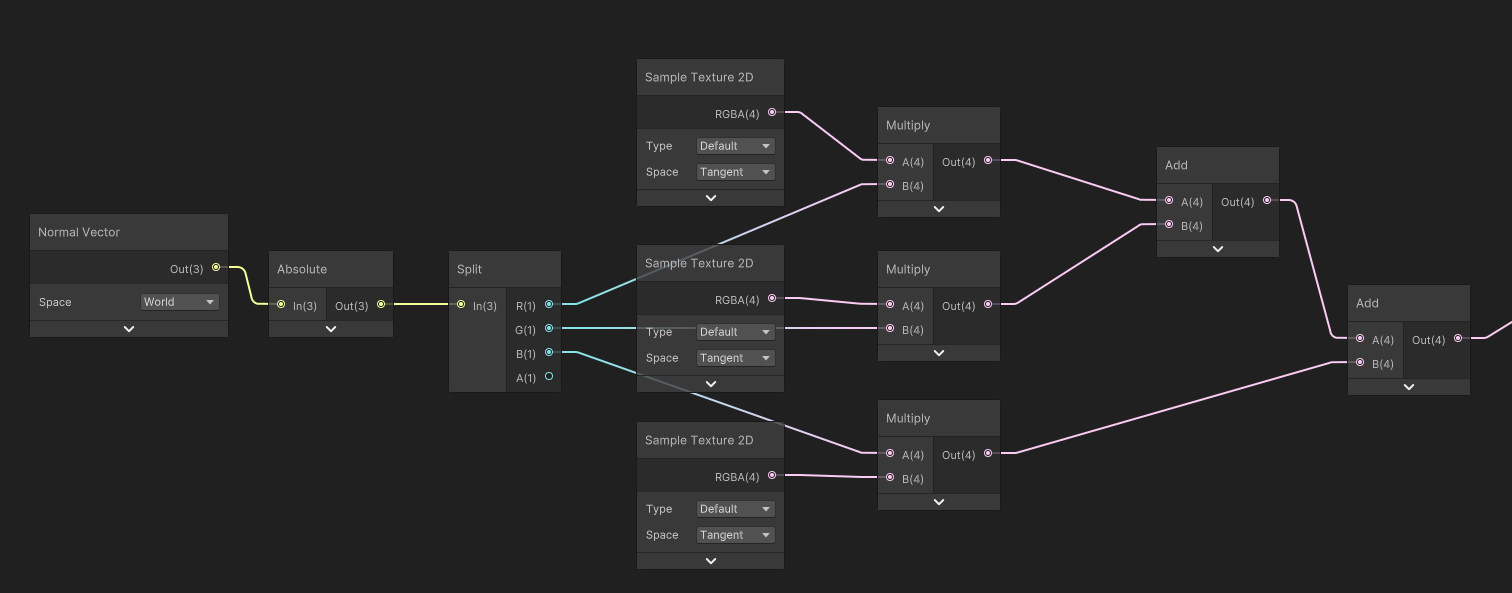
add 해주는 이유:안 하면 마스킹 된 영역만 제대로 보여지고 나머지는 검정 색으로 보임.
인터넷에 무료로 올라와있는 텍스쳐 가져와서 넣어주면! 이렇게 보인다.
3. 월드 UV를 알아보자
이걸 하는 이유는 내가 만들고자 하는 쉐이더의 목표가 모든 텍스쳐가 월드 포지션을 UV로 갖게끔 만들어야 했기 때문이다. 눈이나 사막 모래가 쌓이는 연출을 하고자 한다면 세 면 다 구하는 게 아닌 윗면 UV만 알아도 충분할 것 같다.
이제 월드 포지션 기준의 UV를 알아보자!
UV는 텍스쳐가 들어갈 float2 값을 알아내야 하니까, 다음 이미지 처럼 알면 되겠다.

3D 모델 이미지는 블렌더에서 가져온지라 z축 방향 색상이 y 초록색이다.
유니티 방향에 맞게 표시를 했다.노드로는 이렇게 표현한다.
Position 노드를 만들고, Space를 World로 설정, 이 값을 split 해주고 vector2 노드 3개를 생성해 각각 (x,y) (x,z), (z,y)를 in 값에 넣어준다.

그리고 프로퍼티에서 텍스쳐를 받아올 수 있게 Texture2D들을 생성해준다. 쉽게 구분하기 위해 프로퍼티 이름을 Red, Green, Blue로 설정했다.
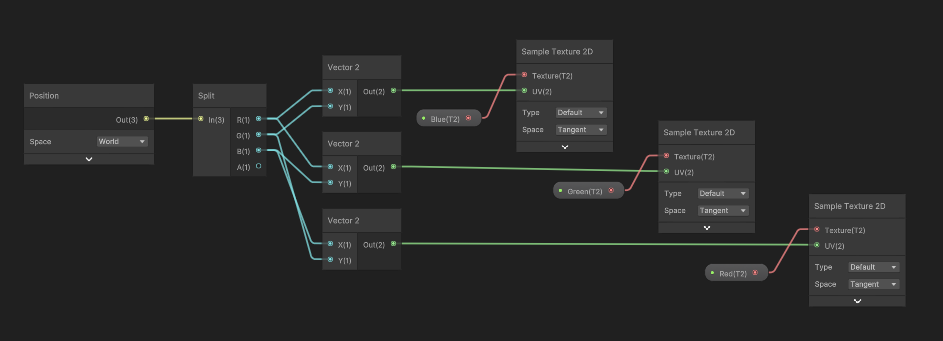
다음 이미지처럼 연결해준다.
xy를 uv갖는 vector2 => Blue 텍스쳐의 UV
zy를 uv갖는 vector2 => Green 텍스쳐의 UV
xv를 uv갖는 vector2 => Red 텍스쳐의 UV
각각의 UV를 갖는 텍스쳐들을 직접 렌더링 해보자.
월드 포지션의 XZ를 UV로 갖는다면 다음처럼 보인다.

XZ값 (Y방향, 초록색 영역)의 UV는 가지고 있지만, 옆면 값이 없기 때문에 길게 늘어진 것처럼 보인다.
XY(Z방향, 파란색 영역), ZY (X방향, 빨간색 영역)은 다음과 같이 보인다.

이제 UV를 갖는 오브젝트에 2에서 구했던 마스킹 영역을 곱해주어 전부 더해주면! 된다.

결과물
사실 3에서의 결과물은 2와 똑같아 보이긴 하다. 하지만, 월드 포지션을 UV로 갖기 때문에 형태가 실시간으로 바뀌어도 텍스쳐가 늘어나거나 왜곡되는 현상이 없다!
이것 때문이라도 귀찮은 UV 계산을 해줄 필요가 있었다.

참고로 Sphere에 넣으면 이렇게 보인다.

- 참고 자료
PolyToots : https://www.youtube.com/watch?v=yuiQo54Baos&ab_channel=PolyToots
