1. 빈도주의와 차이점
- 빈도주의는 point estimate로 시점이 고정되어 있음
- 베이지안은 ditribution estimate로 사후 확률을 통해 측정하려는 확률이 실시간으로 업데이트됨
2. 주요 아이디어
- 일정 조건 하에서 어떤 사건이 일어날 <조건부 확률>에 관한 개념임
- A라는 조건에서 B가 일어날 확률을 구하기 위해서 A가 일어날 표본 공간 안에서 A와 B의 교집합을 구하는 집합의 개념을 이용함
- 어떤 사건이 일어날 가능성을 다룰 때 민감도(TP)와 특이도(TN)의 영향력을 고려함
3. 베이지안 정리
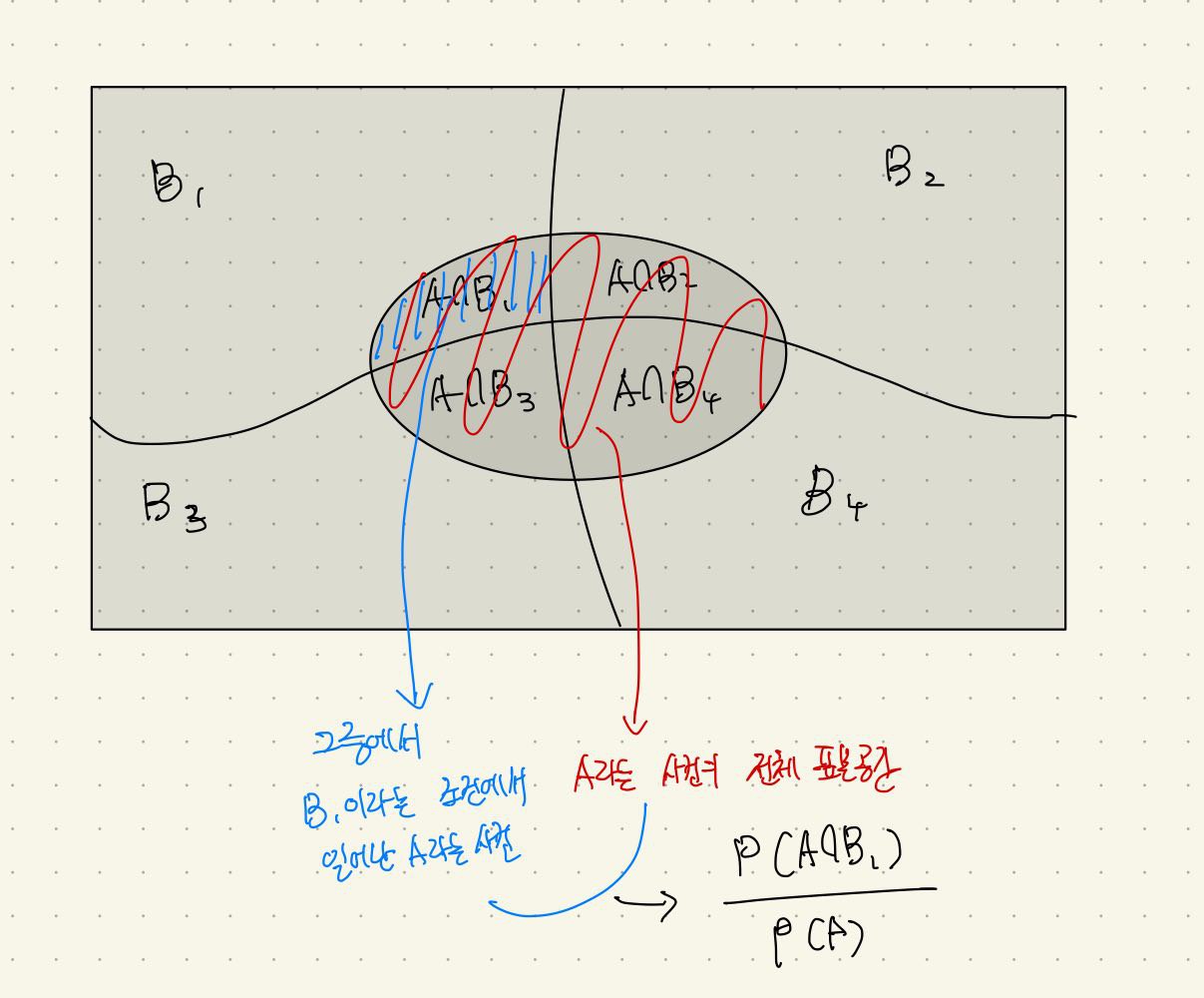
- B라는 조건에서 A가 일어날 확률은 B가 일어날 표본 공간 안에서 B와 A의 교집합을 의미함
P(A|B) = P(A∩B) / P(A)
-> P(A∩B) = P(B|A)*P(A) #P(A∩B) = P(B∩A)
-> P(A) = P(B|A)*P(A) + P(B|A^)*P(A^) #A라는 사건이 일어나는 전체 표본공간을 의미함
P(A|B) = P(B|A)*P(A)/P(B|A)*P(A) + P(B|A^)*P(A^) #베이지안 정리- 이때 P(A)는 사후확률로 계속 업데이트되는 확률임
- P(B|A)는 우도(likehood)로 고정되어 있는 확률임(ex. 항체 테스트기의 양성 판독률 자체는 변하지 않음)
4. python 구현
- 특정 범죄수사 단계에서 형사는 특정 용의자의 유죄를 60% 확신한다.
- 이제 범죄자가 왼손잡이임을 보여주는 새로운 증거가 발견되었다고 가정한다.
- 인구의 20%가 이 특성(왼손잡이)을 가지고 있고, 용의자가 이 그룹에 속해 있는 것으로 판명되면 형사는 용의자의 유죄를 얼마나 확신해야 합니까?
#A = 용의자가 범인일 사건
#B = 누군가가 왼손잡이일 사건
#P(A|B) = 왼손잡이가 범죄자일 확률
#P(B|A) = 범죄자가 왼손잡이일 확률 -> 1
#P(B|A`) = 범죄자가 아닌 누군가 왼손잡이일 확률 -> 0.2
#P(A) = 0.6
#P(A`) = 1 - P(A)
#베이지안 정리 : P(A|B) = P(B|A)*P(A) / P(B|A)*P(A) + P(B|A`)*P(A`)
a = (1 * 0.6) / ((1 * 0.6) + (0.2 * 0.4))
print(a)
5. 어디서 어떻게 쓰일까?
- 주행 시 주기적으로 도로 정보 등을 스캔하여 현재 상황에서 벌어질 수 있는 일들의 확률을 구함.
- 이때 현재 상황이 전체 표본 공간이고, 현재 상황에서 벌어질 수 있는 어떤 일은 조건부 확률을 의미함. 우도는 이 현장에서 어떤 사건이 벌어진(!) 확률임
- 이 세가지 개념으로 사전 확률을 계산함
- 확률에 따라 사건을 계산하고, 예측했던 사건의 결과에 따라 사후 확률을 업데이트함
-