백준 / 9249 / python / 최장 공통 부분 문자열

NakTa·2021년 11월 30일

필요한 사전지식

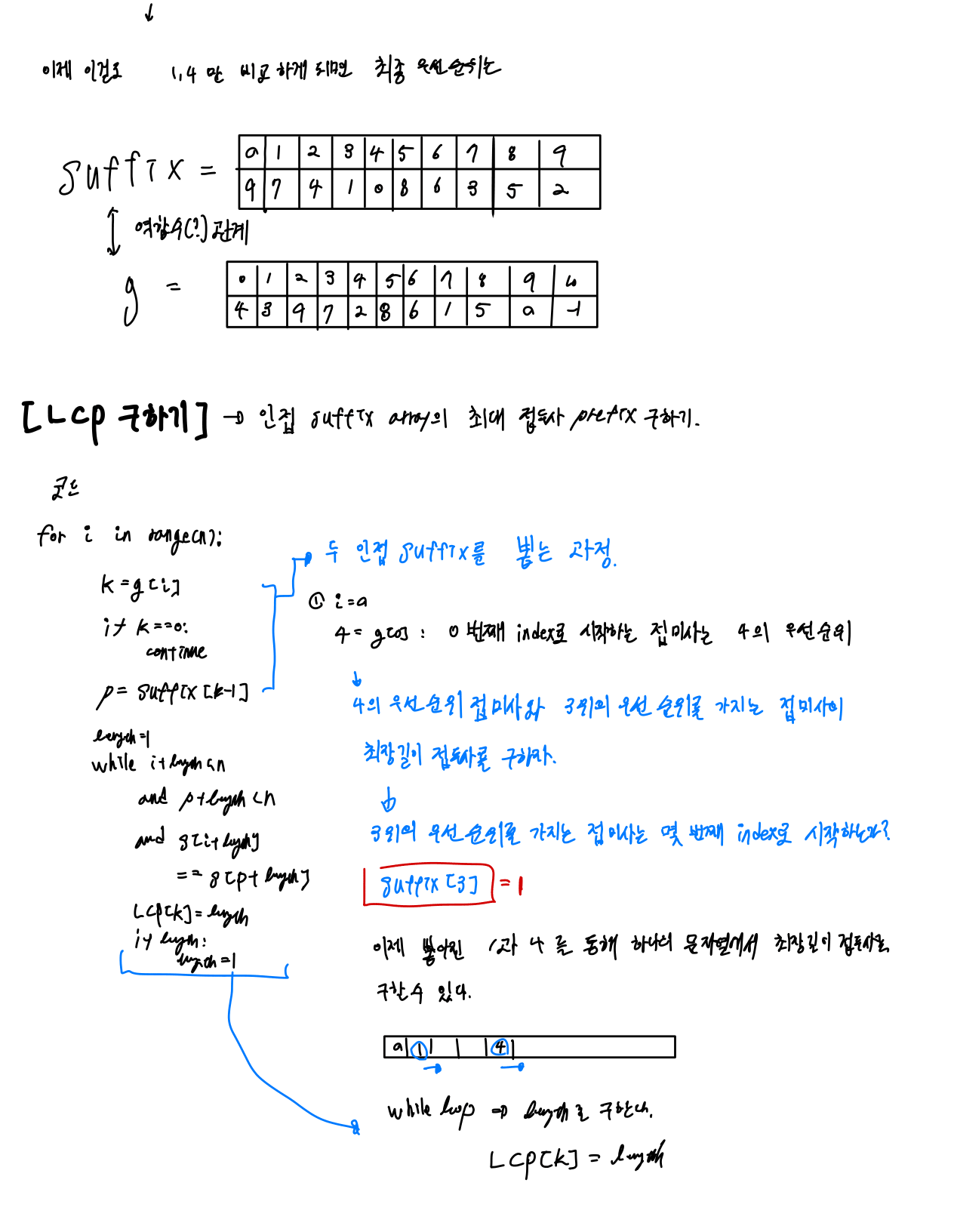
1) suffix array : 시간 복잡도를 줄이기 위해 맨버-마이어스 알고리즘(Manber-Myers Algorithm)로 구현해야 한다.
2) lcp

문제를 해결하기 위해 이해해야 할 것들

lcp 배열에서 최대값은 중복되는 가장 긴 부분 문자열의 길이이다.

suffix array는 lcp를 구하기 위한 과정의 하나이다. suffix array는 접미사들을 사전 순으로 정렬한 것이고, lcp는 접두사들의 최장 길이를 비교하는 것이기 때문에 lcp는 중복되는 부분 문자열의 값들을 저장하게 된다.

그래서 lcp의 최대값은 가장 긴 중복 부분 문자열의 길이이다.

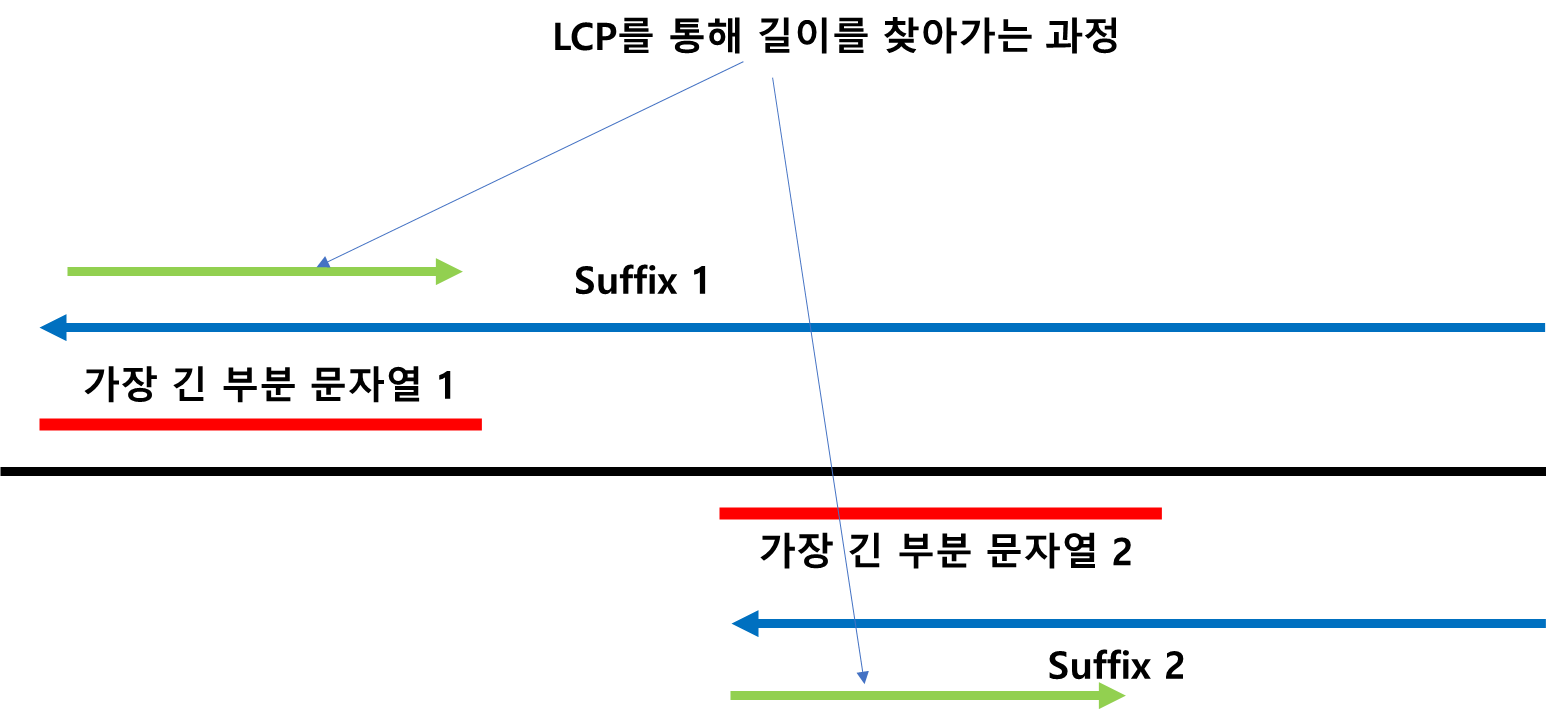
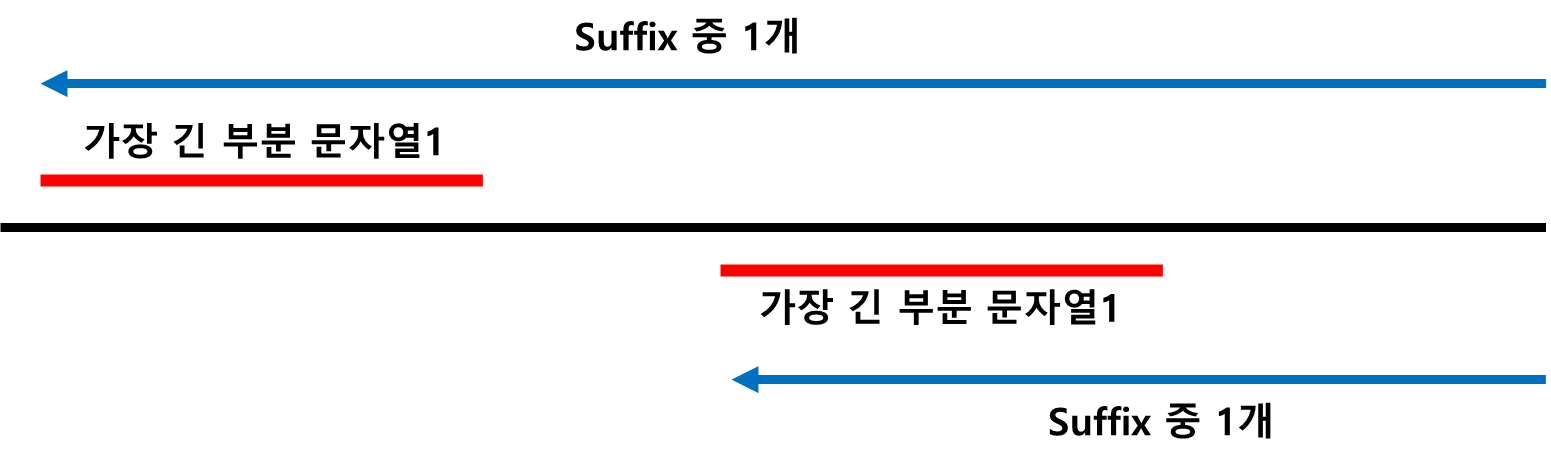
비교될 두 suffix array는 붙어 있을 수 밖에 없다. 왜냐하면 suffix array가 정렬된 기준이 가장 긴 부분이 겹치게 정렬이 되어 있기 때문이다.
ex)
ababababcccc
ababababccccaaasd
ababababdd

문제 풀이 유의사항

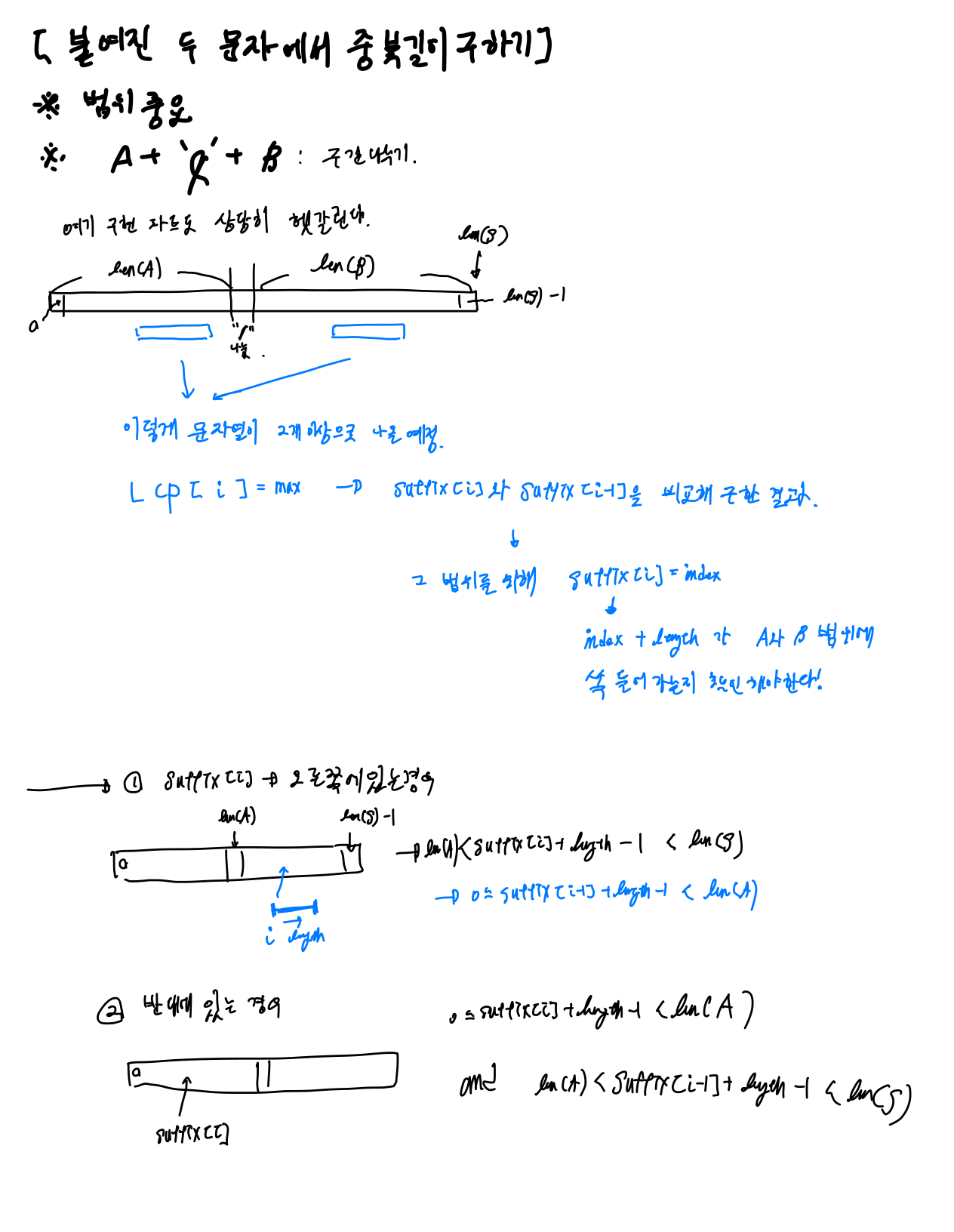
1) A문자열과 B문자열 사이에 '1'또는 '&'과 같은 문자를 추가하여, suffix array를 구하고 lcp를 구하는 과정에서 오류케이스가 생기는 것을 방지

ex)
A = banana
B = ana
A + B = bananaana
A + '1' + B = banana1ana

2) lcp에서 최대값 때 : 서로 다른 영역에서 얻어진 lcp의 값들 중에서 최대값을 구해야 한다.

코드

A = input()
B = input()
s = A +'1' + B
n = len(s)

# Get Suffix Array
suffix = [i for i in range(n)]
g = [0]*(n+1) # 순위
ng = [0]*(n+1) # 새로운 순위를 갱신할 때 이용

for i in range(n):
    g[i] = ord(s[i])

g[n] = -1 
ng[suffix[0]] = 0
ng[n] = -1

t = 1
while t<n:
    suffix.sort( key=lambda x :(g[x], g[min(x+t, n)]) )
    
    for i in range(1, n):
        p, q = suffix[i-1], suffix[i]

        if g[p]!=g[q] or g[min(p + t, n)] != g[min(q + t, n)]:
            ng[q] = ng[p] + 1
        else:
            ng[q] = ng[p]
    
    # 처음 부터 정렬이 바로 되어 있을 때 바로 탈출 하기 위해서
    if ng[n-1] == n-1:
        break


    t= t*2
    g = ng[:]


# Get LCP Array
LCP = [0]*n
length = 0 
for i in range(n):
    k = g[i]
    if k==0: # 처음은 들어가지 않는다.
        continue 
    p = suffix[k-1]

    while i+length < n and p+length <n and s[i+length] == s[p+length]:
        length+=1
    LCP[k] = length

    if length:
        length-=1


# 나누어진 영역에서의 최대값 구하기
m =(0,0) # length, start_index
for i, j in enumerate(LCP):
    if 0<=suffix[i-1] + j - 1<len(A) and len(A) < suffix[i] + j-1 <len(s):
        m = max(m,(j,i))
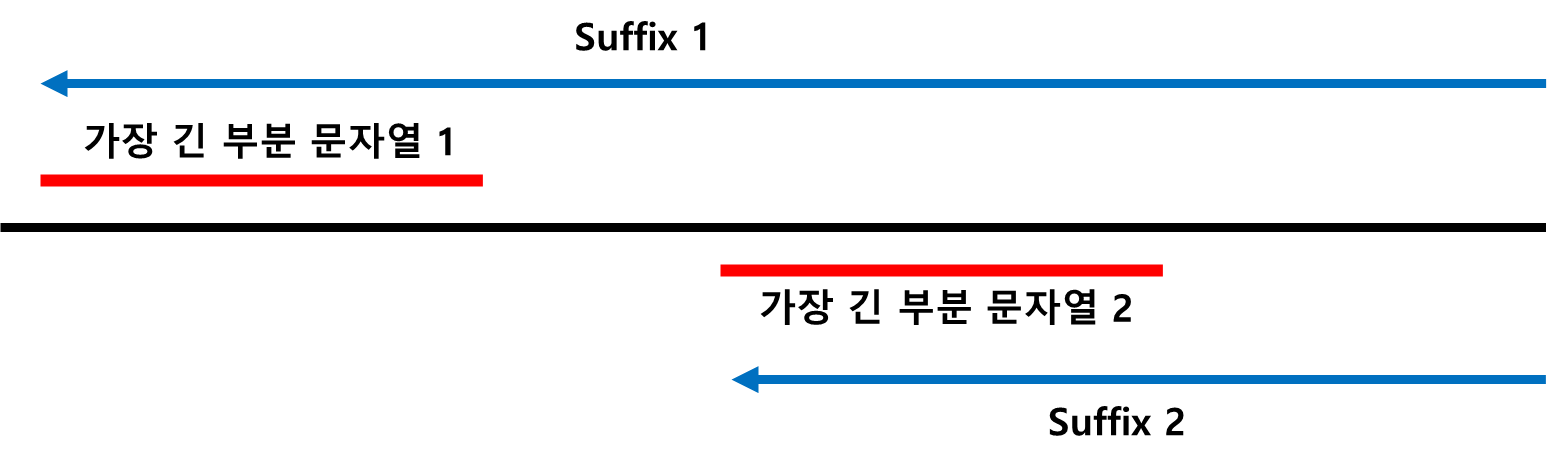
    if 0<=suffix[i] + j - 1<len(A) and len(A) < suffix[i-1] + j-1 <len(s):
        m = max(m,(j,i))
    
length, start = m
print(length)
print(s[suffix[start]: suffix[start] + length])