A Sub-linear, Massive-scale Look-alike Audience Extension System (2016/Yahoo)정리

gorany·2024년 11월 8일

Ad tech

AdTech : Paper Review

목록 보기

1/3

A Sub-linear, Massive-scale Look-alike Audience Extension System

1 Introduction

1.1 Abstraction

유사 유저(look-alike audience) 확장은 온라인 광고에서 고성능 잠재 고객(high performance audience)를 맞춤 설정할 효과적인 방법입니다.
look-alike audience 시스템을 통해, 광고주는 복잡한 광고 시스템에서 타겟 속성에 대해 구체적으로 알 필요 없이, 기존 고객 목록만 제공하면 맞춤형 오디언스를 쉽게 생성할 수 있습니다.
논문에서는 야후 광고 플랫폼에서 수천 개의 캠페인에 대해 look-alike audience 를 제공하는 새롭게 개발된 그래프 기반 룩어라이크 시스템을 소개함.
실험 결과, 최근접 이웃 필터링(nearest-neighbor filtering)을 활용한 그래프 기반 방법이 앱 설치 광고 캠페인에서 전환율 측면에서 다른 방법들에 비해 50% 이상 우수한 성과를 나타냄.

1.2 Introduction

look-alike audience 는 어떤것인가?

온라인 광고 캠페인에서 look-alike audience 모델을 사용하면 광고주가는 기존 고객과 유사한 사용자들에게 다가갈 수 있음.
- Ex : 과거 구매자, 웹 서비스 구독자, 특정 앱 설치자, 브랜드 애호가, 고객 관계 관리(CRM) 시스템의 고객, 광고 클릭자 등
look-alike audience 는 광고 타겟팅을 복잡하게 하는것 보다 매우 관련성 높은 사람들에게 더 "쉽게" 도달할 수 있다는 점
- 광고주는 사용자의 특정 속성에 대한 상세 정보를 알지 않고도 사용자 목록을 업로드하여 맞춤형 오디언스를 생성할 수 있음.
look-alike audience 시스템의 inpt 값은 "시드"라 불리는 User-ID List (예: 브라우저 쿠키, 주소, 전화번호 또는 기타 식별자)입니다.
- 이 시드 사용자는 광고주의 과거 캠페인에서의 전환자일 수도 있고, 더 높은 구매력을 가진 기존 고객일 수도 있습니다.
출력은 룩어라이크 모델에 따라 시드와 유사하다고 판단되는 사용자 목록입니다. 이후 광고주는 이처럼 선정된 룩어라이크 오디언스를 대상으로 광고를 캠페인에서 노출할 수 있습니다.

유사 유저의 효과는 어떻게 측정되는가?

확장성 : Scalability
- 유사 타겟(look-alike audience) 출력의 최대 크기는 어느 정도인가요?
- 유사 타겟 생성에 적절한 결과를 가져올 수 있는 시드(seed)의 양은 상한선과 하한선이 어떻게 되나요?
성능 : Performance
- 광고주가 시드 목록을 업로드한 후, 시스템이 얼마나 빠르게 유사 타겟을 생성할 수 있는지?
- 실제 광고 캠페인에서 유사 타겟이 얼마나 높은 투자 대비 수익(ROI)을 달성할 수 있나요?
투명성 : Transparency
- 이 시스템은 블랙박스처럼 작동하는가?
- 광고 캠페인 설정 과정에서 피드백과 인사이트를 생성할 수 있는가 (model Interpretebility와 연결)?
- 이런 피드백과 인사이트는 얼마나 빠르게 생성될 수 있나요? 몇 초 이내?, 아니면 며칠?
즉, 확장성, 성능, 모델 투명성에 대한 요구 사항이 서로 다르기 때문에, 유사 타겟 확장 시스템의 "유일한 최적 설계"는 존재하지 않습니다.

본 연구(Yahoo)의 주요 기여점은 다음과 같습니다.

대규모 유사 타겟 확장 시스템 제시
- Yahoo!에서 구축한 대규모 유사 타겟 확장 시스템을 소개.
- 이 시스템은 쿼리 대상 사용자 수에 대해 서브-선형(sub-linear)의 유사 사용자 쿼리 시간을 보임.
- 핵심 모델은 사용자 간(pairwise user-2-user) 유사성에 기반한 그래프 마이닝과 머신러닝 기술을 활용하며, 3시간 이내에 30억 명 이상의 사용자와 3000개 이상의 캠페인을 스코어링할 수 있습니다.
실험을 통한 성능 검증
- 실제 앱 설치 캠페인 데이터를 활용한 광범위한 실험을 통해, 제안된 방법이 기존의 다른 유사 타겟 확장 모델보다 앱 설치율을 50% 이상 높일 수 있음을 보여줍니다.
개발 과정에서의 도전 과제 및 경험 공유
- 대규모 유사 타겟 확장 시스템을 개발하는 과정에서의 도전 과제와 경험을 공유합니다.
- 가중치가 적용된 사용자 간 유사성 그래프(weighted user-2-user similarity graph)를 활용하면, 앱 설치율을 추가적으로 11% 더 개선할 수 있음을 입증합니다.

1.3 Existing Look-alike Methods & Systems

두 사용자의 유사성(look-alikeness)은 **유저의 특징(feature)을 기반으로 측정됩니다. 사용자 $u_i$ 는 특징 벡터 $\mathbf{f}_i=\left(f_{i, 1}, \cdots, f_{i, K}\right)$ 로 표현될 수 있습니다. 온라인 광고 시스템에서는 각 특징 $f_{i, k}$ 가 다음과 같은 유형일 수 있습니다.

연속형(continuous): 예를 들어, 특정 사이트에서 소비한 시간 등.
범주형(categorical) 또는 이진형(binary): 예를 들어, 특정 모바일 앱을 사용했는지 여부 등.

특징(Feature)은 다음과 같은 다양한 소스에서 나올 수 있습니다.

사용자의 속성(attributes)
행동(behaviors)
소셜 상호작용(social interactions)
미리 정의된 오디언스 세그먼트(pre-built audience segments) 등

또한, 기업마다 사용자에 대한 비즈니스 요구와 이해 방식에 따라 사용자를 표현하는 데 사용하는 특징이 다를 수 있 습니다.

특징 벡터의 차원은 수천 개에서 수백만 개까지 다양할 수 있습니다. 본 논문에서는 $f_{i j} \in\{0,1\}$ 인 경우를 고려하며, 연속형 특징은 필요한 경우 여러 개의 이진 특징(binary features)으로 버킷화(bucketized)됩니다.
우리가 알고 있는 한, 온라인 광고 업계에서 사용되고 있는 유사 타겟 시스템은 크게 세 가지로 분류될 수 있습니다
- 단순 유사성 기반 모델
- 회귀 기반 모델
- 세그먼트 근사 기반 모델.

1.3.1 Simple Similarity-based Look-alike System

유사 타겟 사용자를 찾는 단순한 방법은 시스템 내의 시드 사용자와 사용 가능한 모든 사용자 쌍을 비교한 뒤, 거리 측정을 기반으로 유사성을 판단하는 것입니다.
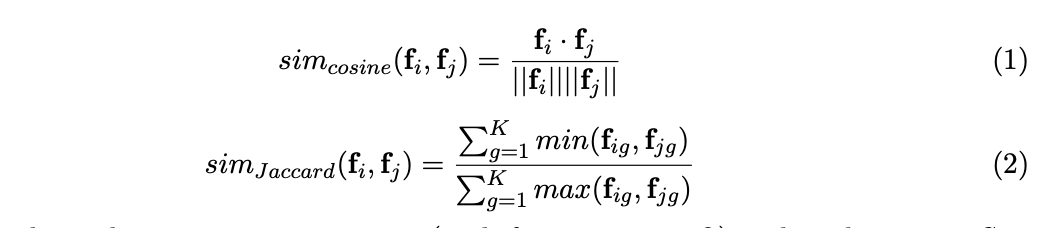
단순 유사성 기반 유사 타겟 시스템은 사용자 간 직접적인 유사성(user-2-user similarity)을 활용하여 시드와 유사한 사용자들을 탐색할 수 있습니다. 두 사용자 $u_i$ 와 $u_j$ 의 유사성은 이들의 특징 벡터(feature vector) $\mathbf{f}_i$ 와 $\mathbf{f}_j$ 를 기반으로 정의됩니다: $\operatorname{sim}\left(\mathbf{f}_i, \mathbf{f}_j\right)$ .

유사성을 측정하는 방법으로는 다음 두 가지가 가능합니다:

코사인 유사도 (Cosine similarity): 연속형 특징에 사용되며, 수식은 위 그림의 Equation 1로 표현됩니다.
자카드 유사도 (Jaccard similarity): 이진 특징(binary features)에 사용되며, 수식은 Equation 2 로 나타 냅니다.

주어진 사용자 $u_i$ (특징 벡터 $\mathbf{f}_i$ )와 시드 사용자 집합 $S=\left\{u_j: \mathbf{f}_j\right\}$ 간의 유사성은 해당 사용자가 시드 집합에서 가장 유사한 사용자와의 유사도로 계산할 수 있습니다. 이때 유사성은 다음과 같이 정의됩니다:

\operatorname{sim}\left(\mathbf{f}_i, S\right)=\max _{\mathbf{f}_j \in S} \operatorname{sim}\left(\mathbf{f}_i, \mathbf{f}_j\right)

더 복잡한 방법으로는 사용자 간 유사도(user-2-user similarity) 측정값을 확률적으로 집계하는 방법이 있습니 다. 이 방법은 유사도 값이 반드시 0 과 1 사이로 제한되는 경우에만 적용 가능합니다. 이 경우, 사용자 간 쌍별 유사도는 "유사 타겟"으로 분류될 확률로 간주됩니다. 따라서, 특정 사용자와 시드 집합 간 의 유사성은 다음 식으로 계산됩니다:

\operatorname{sim}\left(\mathbf{f}_i, S\right)=1-\prod_{\mathbf{f}_j \in S}\left(1-\operatorname{sim}\left(\mathbf{f}_i, \mathbf{f}_j\right)\right)

수식에서 $\prod_{\mathbf{f}_j \in S}\left(1-\operatorname{sim}\left(\mathbf{f}_i, \mathbf{f}_j\right)\right)$ 은 "유사하지 않을 확률"을 나타내며, 이를 1 에서 빼면 "유사할 학률"이 됩니다. 단순 유사성 기반 방법은 소규모에서 구현하기 쉽고, 사용자 특징 공간에서 모든 시드가 가진 정보를 활용할 수 있다 는 장점이 있습니다. 그러나 이 방법에는 다음과 같은 주요 문제점이 있습니다.

1.확장성 문제 (Scalability)

많은 수의 사용자 간 유사성을 쌍별로 계산하는 것은 간단하지 않습니다.
완전 탐색(brute force) 방식의 계산 복잡도는 $O(k M N)$ 로, 여기서 $N$ 은 후보 사용자 수, $M$ 은 시드 수, $k$ 는 사용자당 평균 특징 수를 나타냅니다.
일반적인 온라인 광고 시장에서는 후보 사용자가 수십억 명에 이르고, 시드가 수만 개 이상이며, 사용자당 수백 개의 특징을 가지기 때문에 계산량이 매우 큽니다.

2.특징의 중요도 무시 (Feature Importance Ignored)

시드 사용자의 다양한 특징들이 동일하게 취급되며, 가장 관련성이 높은 후보 사용자를 식별하는 데 있어 각 특징의 영향력이 구분되지 않습니다.
예를 들어, 광고 클릭(ad clicks) 또는 전환(conversions)을 예측하는 데 중요한 특징과 그렇지 않은 특징이 동일한 가중치를 받습니다.
이로 인해, 별로 중요하지 않은 특징에 기반한 유사성 때문에 관련성이 낮은 후보 사용자가 유사 타겟으로 간주될 수 있습니다.

1.3.2 Regression-based Look-alike System

온라인 광고에서 또 다른 유형의 유사 타겟 시스템은 로지스틱 회귀(Logistic Regression, LR)를 기반으로 구 축됩니다(Qu et al., 2014). 주어진 사용자 $u_i$ 가 특징(Feature) 벡터 $\mathbf{f}_i$ 를 가지고 있을 때, 로지스틱 회귀 모델은 해당 사용자가 시드와 유사할 확률을 다음과 같이 모델링할 수 있습니다

p\left(u_i \text { is a lookalike to seeds } \mid \mathbf{f}_i\right)=\frac{1}{1+e^{-\mathbf{f}_i^{\prime} \beta}}

여기서 "시드(seeds)"는 일반적으로 양성(positive examples) 로 간주됩니다. 반면, 음성(negative examples)를 선택하는 방법에는 여러 가지가 있습니다:

1.단순 샘플링:

음성 사례로 시드가 아닌 사용자의 샘플을 선택합니다.
그러나 이 방법은 최적의 선택이 아닐 수 있습니다. 시드에 포함되지 않은 사용자 중에도 광고를 클릭하거 나 전환할 가능성이 있는 사용자가 포함될 수 있기 때문입니다.

2.광고 서버 로그 활용:

과거에 광고주의 광고를 본 적이 있으나 전환하지 않은 사용자를 음성 사례로 선택할 수 있습니다.
그러나 이 방법은 콜드 스타트 문제(cold start problem) 가 발생할 수 있습니다.
예: 시드가 새로운 광고주에서 나온 경우, 또는 새로운 광고 캠페인에 사용될 경우, 해당 광고를 본 사용자가 존재하지 않을 수 있습니다.

특징(Feature) 선택(feature selection)

특징(Feature)의 수가 많을 경우, 손실 함수에 $L_1$ 정규화를 적용하여 최종 모델에서 0이 아닌 값의 수를 줄임으로써 특 징 선택(feature selection)을 수행합니다.
실제로는 Vowpal Wabbit과 같은 머신러닝 패키지를 사용하여 수백만 개의 특징(Feature)을 포함한 대규모 데이터에서 Hadoop 클러스터 상에서 로지스틱 회귀를 학습시키고, 대량의 사용자에 대해 이러한 확률을 예측할 수 있습 니다.

이 모델링 방법의 장점은 시드가 가진 정보를 하나의 모델(예: $\beta$ )로 압축할 수 있다는 점입니다. 이를 통해 유사 타 겟 여부를 평가할 때 시드의 특징(Feature) 벡터를 따로 기억할 필요가 없습니다. 이러한 큰 이점에도 불구하고, 로지스틱 회 귀와 같은 회귀 모델을 유사 타겟 문제에 적용할 때 몇 가지 잠재적인 한계가 존재합니다.

로지스틱 회귀(LR)는 선형 모델이기 때문에, 많은 결합(conjunctions), 교차(cross) 또는 기타 의존성을 특징(Feature)에 포함시킬 수는 있지만, 사용자들을 군집화(clustering)하는 데 있어 완벽하거나 효율적이지 않을 수 있습니다.

1.3.3 Segment Approximation-based Look-alike System

또 다른 유형의 유사 타겟 시스템은 사용자 세그먼트 근사(User Segment Approximation)를 기반으로 합니다. 여기서 사용자 세그먼트란 사용자의 관심사 카테고리와 같은 특성을 의미합니다. 예를 들어, 한 사용자가 NBA 경기를 좋아한다면, 이 사용자는 스포츠(Sports) 세그먼트에 속한다고 간주됩니다.

다른 방법과 비교했을 때, 세그먼트 근사 기반 시스템은 미리 구축된 사용자 세그먼트(pre-built user segments)를 사용자 특징(Feature)으로 활용합니다. 이 방법의 일반적인 아이디어는 시드 사용자들 중 가능한 많은 수가 "공유"하는 주요 세그먼트를 찾아내는 것 입니다.

이를 통해 유사한 관심사나 특성을 가진 사용자 그룹을 더 쉽게 식별할 수 있습니다. 여기서는 Turn Inc.의 Shen et al. (2015)에서 발표한 세그먼트 근사 기반 방법 중 가장 최근의 연구를 다룹니다. 이 접근법에서, 각 사용자는 세그먼트들의 집합(bag of segments)으로 표현됩니다:

u_i=\left\{c_{i 1}, \cdots, c_{i K}\right\}

유사 타겟 확장(look-alike audience extension)의 최적화 목표 광고주가 제공한 세그먼트 집합 $C$ (즉, 시드 사용자에서 나타나는 세그먼트들)가 주어졌을 때, 다음 세 가지 속성을 만족하는 새로운 사용자 세그먼트 집합 $C^{\prime}$ 를 추천하는 것입니다:

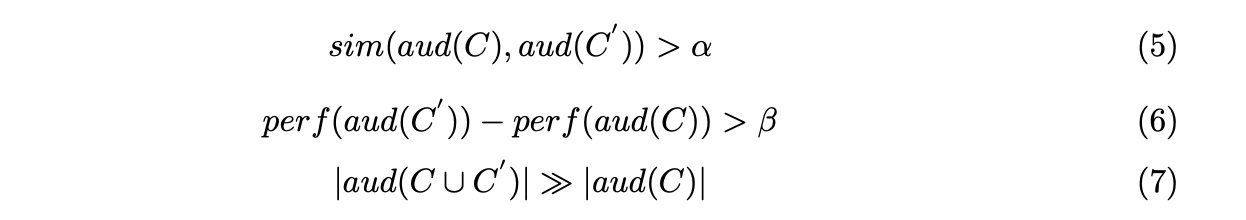
용어 설명:

$\operatorname{aud}(C)$ :
- 세그먼트 $C$ 에 해당하는 사용자의 집합. 즉, $C$ 중 하나라도 포함된 사용자를 나타냄.
$\operatorname{perf}(\operatorname{aud}(C))$ :
- 사용자 집합 $\operatorname{aud}(C)$ 의 성능. 예를 들어, 광고 클릭률(Click-Through Rate, CTR)이나 전환율 (Conversion Rate, CR) 등.

조건의 의미:

유사성 조건 (sim):
- 확장된 세그먼트 집합 $C^{\prime}$ 에 해당하는 사용자 집합 $\operatorname{aud}\left(C^{\prime}\right)$ 은 시드 세그먼트 집합 $\operatorname{aud}(C)$ 과 충분히 "유사"해야 함.
- 즉, 두 집합 간의 사용자 겹침 정도(중복률)가 특정 임계값 $\alpha$ 이상이어야 함.
성능 향상 조건 (perf):
- 확장된 세그먼트 집합 $\operatorname{aud}\left(C^{\prime}\right)$ 의 성능(예: 클릭률, 전환율 등)이 기존 세그먼트 집합 $\operatorname{aud}(C)$ 의 성능 보다 최소 $\beta$ 만큼 더 높아야 함.
확장성 조건 $(|\cdot|):$
- 확장된 사용자 집합 $\operatorname{aud}\left(C \cup C^{\prime}\right)$ 은 기존 사용자 집합 $\operatorname{aud}(C)$ 에 비해 훨씬 더 큰 크기를 가져야 함.
- 이는 광고 캠페인의 타겟 범위를 효과적으로 확장하는 것을 목표로 합니다.

위 조건들을 만족하는 세그먼트가 여러 개 있을 수 있으므로, 세그먼트의 중요도를 구분하기 위한 점수 함수 (scoring function) 가 필요합니다. Shen et al. (2015)에서는 탐욕적(greedy) 접근법을 논의하였으며, 이는 집합 커버 알고리즘(set cover algorithm)의 응용과 가중치 기반 기준(weighted criteria-based) 알고리즘을 포함합니다.

새로 추천된 세그먼트(또는 카테고리) $c_{\text {new }}$ 에 대해, 세 가지 함수(Eq. 5, 6, 7)를 조합하여 다음과 같은 점수를 계산합니다:

\operatorname{score} \propto \operatorname{sim}\left(\operatorname{aud}\left(c_{\text {new }}\right), \operatorname{aud}(C)\right) \times \operatorname{perf}\left(\operatorname{aud}\left(c_{\text {new }}\right)\right) \times \operatorname{nov}\left(\operatorname{aud}\left(c_{\text {new }}\right) \mid \operatorname{aud}(C)\right)

여기서,

$\operatorname{sim}\left(\operatorname{aud}\left(c_{\mathrm{new}}\right), \operatorname{aud}(C)\right)$ : 새로운 세그먼트와 기존 시드 세그먼트 간의 유사성을 측정합니다.
$\operatorname{perf}\left(\operatorname{aud}\left(c_{\mathrm{new}}\right)\right)$ : 새로운 세그먼트에 속하는 사용자의 성능(예: 클릭률, 전환율 등)을 평가합니다.
$\operatorname{nov}\left(\operatorname{aud}\left(c_{\mathrm{new}}\right) \mid \operatorname{aud}(C)\right)$ : 새로운 세그먼트 $c_{\mathrm{new}}$ 에 속하는 사용자 중 기존 시드 사용자에 포함되지 않 은 사용자의 비율을 측정합니다(신규성 측정).

위 점수에 따라 모든 사용자 세그먼트를 정렬한 후, 상위 $k$ 개의 세그먼트를 광고 캠페인의 타겟으로 추천합니다. (더 자세한 내용은 Shen et al. (2015)를 참고)

세그먼트 근사법은 사전 구축된 세그먼트의 품질이 높고 커버리지가 충분한 경우 효과적으로 작동합니다.
이 방법은 특히 대형 브랜드 광고주(big branding advertisers)에게 적합하지만, 소규모 광고주(small advertisers)에게는 상대적으로 덜 유용할 수 있습니다.

또한, 사전 구축 과정은 추가적인 계산 파이프라인을 도입하게 되어 유사 타겟 생성 시간이 지연될 가능성을 초래할 수 있습니다. 본 논문에서는 위에서 설명한 알고리즘을 구현하여, 대규모 비교 실험 시에 비교군으로 활용했습니다.

2 Graph-Constraint Look-Alike System

이 섹션에서는 우리가 개발한 그래프 제약(graph-constraint) 유사 타겟 시스템의 세부 사항을 소개합니다. 이 시스템은 단순 유사성 기반 방법과 회귀 기반 방법의 장점을 결합한 형태입니다.

시스템 개요

전역 사용자-사용자 유사성 그래프(Global User-2-User Similarity Graph) 생성:
- 시드(seeds)의 가장 가까운 이웃(nearest neighbors)으로 후보 유사 타겟 사용자를 제한할 수 있도록 전역적인 사용자 유사성 그래프를 구축합니다.
특징(Feature) 중요도 기반 랭킹:
- 후보 사용자들은 특정 광고 캠페인(ad campaign)에 따라 중요한 특징(feature importance) 값으로 순위가 매겨집니다.

기존 접근 방식의 비효율성

광고 캠페인별로 모든 사용자에 대해 유사 타겟을 학습(training)하고 점수화(scoring)하는 기존 방식은 비효율적입니다.
- 일반적인 유사 타겟 크기는 1백만~1천만 명으로, 전체 사용자 풀(약 10억 명)의 0.1%~1% 에 해당합니다.
- 이처럼 많은 관련 없는 사용자를 점수화하는 것은 상당한 계산 자원을 낭비하게 됩니다.
- 또한, 99% 이상의 관련 없는 사용자에 대해 학습하여 특징(Feature) 가중치(feature weights)를 얻는 과정은 사용자 샘플링(user sampling) 문제를 야기합니다.

제안된 접근법: 두 단계 생성 과정

전역 그래프 구축 (Global Graph Construction):
- 모든 사용자를 포함하는 유사성 그래프를 생성하여, 후보 사용자 범위를 시드의 가까운 이웃으로 한정합니다.
캠페인별 모델링 (Campaign-Specific Modeling):
- 특정 광고 캠페인에 맞춰 후보 사용자를 평가하고 최종적으로 유사 타겟을 생성합니다.

2.1 Phase I: Global Graph Construction

이 단계에서는 시스템 내 모든 사용자를 대상으로 사용자-사용자(user-2-user) 유사성 그래프를 생성합니다. 두 사용자 간의 연결(edge)은 이들의 자카드 유사도(Jaccard Similarity, Eq. 2)**를 나타냅니다.

이 그래프의 목표는 특정 시드 집합(seeds)과 관련된 유사 타겟 후보를 찾는 것입니다. 우리 접근법의 핵심은 가중치가 부여된 사용자-사용자 간 유사성(pairwise weighted user-2-user similarity)을 다음과 같이 정의하는 것입니다:

\operatorname{sim}\left(\mathbf{f}_i, \mathbf{f}_j\right)=\frac{\mathbf{f}_i^{\prime} \mathbf{A} \mathbf{f}_j}{\left\|\mathbf{f}_i\right\| \times\left\|\mathbf{f}_j\right\|}

여기서:

$\mathbf{f}_i, \mathbf{f}_j$ : 사용자 $u_i, u_j$ 의 특징(Feature) 벡터(feature vectors)
A: 가중치 행렬(weight matrix)로, 개별 특징 및 특징 간 쌍(pairwise feature combinations)의 선형 상 관관계 중요도를 반영합니다.
- 만약 $\mathbf{A}$ 가 대각 행렬(diagonal matrix)이라면, 이 공식은 가중 코사인 유사도(weighted cosine similarity)를 나타냅니다.
- 반면, $\mathbf{A}$ 가 비대각 행렬(non-diagonal matrix)이라면, 쌍별 특징 결합(pairwise feature combinations)을 모델링할 수 있습니다.
고차원 특징 결합(higher-order feature combinations)은 대규모이면서 희소한 특징 공간에서는 유용성이 거의 관찰되지 않습니다.
따라서, 유사 타겟 시스템의 과도한 복잡성을 피하기 위해, 특징 모델링은 개별 특징과 쌍별 특징으로만 제한됩니다. 가중치 행렬의 크기는 전체 특징 수에 따라 결정되며, 이는 전체 사용자 수에 비해 상대적으로 적습니다.
이러한 특성 덕분에, 각 광고 캠페인에 대해 특정 가중치 행렬을 생성하여 특징에 대해 더 세밀한 조정을 가능하게 합니다.

전역 사용자-사용자 유사성 그래프를 구축하는 데에는 두 가지 주요 도전 과제가 있습니다.

사용자 간 쌍별 유사도 계산의 높은 복잡성: $O\left(N^2\right)$
유사 사용자 검색의 높은 복잡성: $O(N)$

이 문제를 해결하기 위해, 잘 알려진 Locality Sensitive Hashing (LSH) 기법을 사용합니다. LSH는 사용자 데이터를 한 번만 읽어도 유사한 사용자들을 동일한 클러스터에 배치할 수 있도록 하며, 유사 사용자 검색을 서브-선형(sub-linear) 시간 안에 가능하게 만듭니다.

2.1.1 MinHash Locality Sensitive Hashing (LSH)

Locality Sensitive Hashing (LSH) 기법(Rajaraman et al., 2012)을 사용하면, 각 사용자는 다음 두 단계를 통해 한 번만 처리됩니다:

해시 함수(Hash Functions)를 사용한 변환
- 사용자 특징 벡터를 유사성을 보존하는 signature으로 변환합니다.
- 이 signature는 원래 특징 벡터보다 훨씬 적은 값들로 구성되어, 데이터의 크기를 크게 줄입니다.
클러스터에 사용자 할당
- 생성된 signature(signature)에 따라 사용자를 클러스터에 할당합니다.
- signature 값들은 유사한 사용자들을 동일한 클러스터에 그룹화하며, 이 과정에서 미리 정의된 유사도 임계값(threshold)을 초과하는 사용자들이 함께 묶입니다.
- 이 클러스터링은 특정 확률로 유사성을 보장합니다.

쿼리 처리 방식

쿼리 시, 입력 사용자에 대해 해시를 수행하여 해당 사용자가 속하는 클러스터를 찾습니다.
이후, 해당 클러스터에 포함된 사용자들이 유사 사용자 후보(candidates)가 됩니다.
클러스터 생성과 유사 사용자 검색 모두 사용자별로 수행되며, 사용자 간 쌍별 연산(pairwise operations)은 필요하지 않습니다.

2.1.1.1 MinHash

MinHash는 LSH(Locality-Sensitive Hashing)에서 사용되는 해싱 기법으로, 데이터의 원래 유사도를 높은 확률로 유지하면서 사용자 Feature 공간을 축소하는 데 활용됩니다.
다양한 해싱 방식이 적용될 수 있으며, 예를 들어 코사인 유사도를 근사하기 위해 랜덤 프로젝션(random projection)을 사용할 수도 있고, Jaccard 유사도를 근사하기 위해 MinHash를 사용할 수도 있습니다. 여기에서는 사용자들의 이진 특징(binary features)에 대한 Jaccard 유사도를 계산하기 위해 MinHash를 사용합니다.
MinHash 함수는 다음과 같이 정의됩니다:

h_{\min }\left(\mathbf{f}_i\right)=\underset{x \in(1, \ldots, K), f_{i, x}=1}{\operatorname{argmin}} h(x)

$\mathbf{f}_i$ : 사용자 $u_i$ 의 $K$ -차원 특징 벡터입니다.
$x: \mathbf{f}_i$ 에서 특정 특징의 인덱스를 나타냅니다.
$h(x)$ : 해시 함수로, 인덱스 $x$ 를 임의의 숫자에 매핑합니다. $h:(1, \ldots, K) \rightarrow R$ .
$h_{\min }\left(\mathbf{f}_i\right)$ 는 해시 값 $h(x)$ 가 최소가 되는 특징의 인덱스를 반환하며, 이를 해시 signature(hash signature)이라 고 부릅니다.

MinHash가 Jaccard 유사도를 유지한다는 점은 Rajaraman 등(2012)의 책 Chapter 3에서 증명할 수 있습니 다. 구체적으로, 두 사용자의 MinHash 값이 동일할 확률은 두 사용자 특징 벡터의 Jaccard 유사도와 동일합니다:

\operatorname{sim}_{\text {Jaccard }}\left(\mathbf{f}_i, \mathbf{f}_j\right)=P\left(h_{\min }\left(\mathbf{f}_i\right)=h_{\min }\left(\mathbf{f}_j\right)\right)

즉, 두 사용자의 Jaccard 유사도가 $r$ 라고 하면, 총 $H$ 개의 MinHash 함수를 사용하여 두 사용자를 독립적으로 해싱했을 때, 두 사용자가 동일한 해시 signature을 가질 것으로 기대되는 횟수는 $H \cdot r$ 입니다 즉 자카드 유사도가 높을수록, 같은 해시값이 많이 나올것입니다.

2.1.1.2 EX : 이해를 위한 예시

Jaccard 유사도란?

Jaccard 유사도는 두 집합 사이의 유사도를 측정합니다. 공식은 다음과 같습니다:

\operatorname{Jaccard}(\mathbf{A}, \mathbf{B})=\frac{|\mathbf{A} \cap \mathbf{B}|}{|\mathbf{A} \cup \mathbf{B}|}

A: 집합 A
B : 집합 B
$|\mathbf{A} \cap \mathrm{B}|: A$ 와 $B$ 의 교집합 원소 개수
$|\mathbf{A} \cup \mathrm{B}|: A$ 와 $B$ 의 합집합 원소 개수

MinHash 사용 예시
1. 이진 특징 벡터 준비
사용자 A 와 사용자 B 의 이진 특징 벡터를 만들어 봅시다. 여기서 이진 벡터는 특정 항목(특징)이 해당 사용자에게 존재(1)하거나 존재하지 않음(0)을 나타냅니다.

사용자 A의 특징 벡터: $\mathbf{f}_A=[1,0,1,0,1]$
사용자 B 의 특징 벡터: $\mathbf{f}_B=[1,1,0,0,1]$

2. Jaccard 유사도 계산
우선 $A$ 와 $B$ 의 Jaccard 유사도를 구합니다.

교집합: $[1,0,1,0,1] \cap[1,1,0,0,1]=[1,0,0,0,1] \rightarrow$ 교집합 원소 개수 $=2$
합집합: $[1,0,1,0,1] \cup[1,1,0,0,1]=[1,1,1,0,1] \rightarrow$ 합집합 원소 개수 $=4$
Jaccard 유사도는:

\operatorname{Jaccard}\left(\mathbf{f}_A, \mathbf{f}_B\right)=\frac{2}{4}=0.5

3. MinHash를 적용해 유사도를 근사하기
MinHash를 통해 Jaccard 유사도를 근사해봅시다.

해시 함수 정의
예를 들어, 2 개의 간단한 해시 함수를 정의합니다:

$h_1(x)=(2 x+1) \bmod 5$
$h_2(x)=(3 x+2) \bmod 5$
여기서 $x$ 는 벡터의 인덱스입니다. $h(x)$ 는 인덱스를 난수로 변환하는 역할을 합니다.

각 사용자 벡터에 해시 적용
각 해시 함수에 대해, $f_i$ 에서 값이 1 인 인덱스만 고려하고, 해시 값이 최소인 인덱스를 선택합니다.

사용자 $\mathbf{A}\left(\mathbf{f}_A=[1,0,1,0,1]\right)$

$f_{A, x}=1$ 인 인덱스: $[1,3,5]$
$h_1(x)$ :
- $h_1(1)=(2 \cdot 1+1) \bmod 5=3$
- $h_1(3)=(2 \cdot 3+1) \bmod 5=2$
- $h_1(5)=(2 \cdot 5+1) \bmod 5=1$
  $\rightarrow$ 최소값은 1 , 인덱스 5 .
$h_2(x)$ :
- $h_2(1)=(3 \cdot 1+2) \bmod 5=0$
- $h_2(3)=(3 \cdot 3+2) \bmod 5=4$
- $h_2(5)=(3 \cdot 5+2) \bmod 5=3$
  $\rightarrow$ 최소값은 0 , 인덱스 1.

사용자 $\mathbf{B}\left(\mathbf{f}_B=[1,1,0,0,1]\right)$

$f_{B, x}=1$ 인 인덱스: $[1,2,5]$
$h_1(x)$ :
- $h_1(1)=(2 \cdot 1+1) \bmod 5=3$
- $h_1(2)=(2 \cdot 2+1) \bmod 5=0$
- $h_1(5)=(2 \cdot 5+1) \bmod 5=1$ $\rightarrow$ 최소값은 0 , 인덱스 2 .
$h_2(x)$ :
- $h_2(1)=(3 \cdot 1+2) \bmod 5=0$
- $h_2(2)=(3 \cdot 2+2) \bmod 5=1$
- $h_2(5)=(3 \cdot 5+2) \bmod 5=3$ $\rightarrow$ 최소값은 0 , 인덱스 1 .

4. MinHash 결과 비교

$h_1$ 에서 사용자 A 의 최소값 인덱스: 5 , 사용자 B 의 최소값 인덱스: $2 . \rightarrow$ 같지 않음.
$h_2$ 에서 사용자 A 의 최소값 인덱스: 1 , 사용자 B 의 최소값 인덱스: $1 . \rightarrow$ 같음.

5. 유사도 근사
총 2 개의 해시 함수 중 1 개에서 동일한 MinHash 값을 가졌으므로, 근사 Jaccard 유사도는:

\text { 근사 Jaccard 유사도 }=\frac{1}{2}=0.5

2.1.2 LSH를 활용한 유사 사용자 클러스터링:

$H$ -차원의 signature을 이용해, LSH 방법은 유사한 사용자를 클러스터로 나누는 유연한 방식을 제공합니다.
가장 널리 사용되는 접근 방식은 "AND-OR 스키마"로, 다음과 같이 작동합니다:

1.signature 분할:

$H$ 개의 signature 차원을 $b$ 개의 밴드(bands)로 분할합니다.
각 밴드는 $r$ 개의 signature 차원을 포함하며, 이는 $b \times r=H$ 관계를 만족합니다.

2.사용자 클러스터링:

각 밴드 내에서 동일한 $r$ -차원 signature을 가진 사용자들은 같은 **버킷(bucket)에 속하게 됩니다.
한 사용자는 한 밴드 안에서는 하나의 버킷에만 포함될 수 있습니다.
따라서, 한 사용자는 총 $b$ 개의 버킷에 포함됩니다.

3.후보 사용자 검색:

만약 시드 사용자가 특정 버킷 $b_i$ 에 포함된다면, $b_i$ 에 포함된 모든 사용자를 해당 시드 사용자의 유사 타겟 후보로 간주할 수 있습니다.
이는 전체 사용자 집합에 비해 휠씬 적은 수의 사용자만을 검색 대상으로 만듭니다.

4.정확도 향상을 위한 후처리:

검색된 후보 사용자들에 대해 필요할 경우, 보다 정밀한 순위를 계산하여 최종적으로 유사성을 평가할 수 있습니다.
$b$ 와 $r$ 의 값은 주어진 데이터의 유사성 분포 및 아이템 간 유사성(item-2-item similarity) 임계값에 따라 경험적으로 결정됩니다.

2.1.2.1 EX : 이해를 위한 예시

문제 설정

사용자 3 명 $\left(u_1, u_2, u_3\right)$ 가 있고, 각 사용자는 이진 특징 벡터를 가지고 있습니다.
각 벡터의 차원은 $K=6$ 이며, 이는 6 개의 특징이 있음을 나타냅니다.
예:

\mathbf{f}_1=[1,0,1,0,0,1] \quad \mathbf{f}_2=[1,1,0,0,1,0] \quad \mathbf{f}_3=[0,0,1,1,0,1]

1.MinHash를 사용한 signature 생성

MinHash는 각 사용자 벡터를 해시 값으로 매핑하여 Jaccard 유사성을 보존하는 signature을 생성합니다.
$H=3$ 개의 해시 함수 $\left(h_1(x), h_2(x), h_3(x)\right)$ 를 사용합니다.

해시 함수 예:

h_1(x)=(2 x+1) \quad \bmod 7, \quad h_2(x)=(3 x+2) \quad \bmod 7, \quad h_3(x)=(5 x+3) \quad \bmod 7

여기서 $x$ 는 특징의 인덱스 $(1 \leq x \leq K)$ 입니다.

(a) 사용자 $u_1$ 에 대한 signature

$\mathbf{f}_1=[1,0,1,0,0,1]$ 에서, 값이 1 인 특징의 인덱스는 $\{1,3,6\}$ 입니다.
각 해시 함수에서 최소 해시 값을 계산:
$h_1(x):\left\{h_1(1)=3, h_1(3)=0, h_1(6)=5\right\} \Rightarrow \min =0$
$h_2(x):\left\{h_2(1)=5, h_2(3)=4, h_2(6)=0\right\} \Rightarrow \min =0$
$h_3(x):\left\{h_3(1)=1, h_3(3)=4, h_3(6)=2\right\} \Rightarrow \min =1$

signature: $[0,0,1]$

(b) 사용자 $u_2$ 에 대한 signature

$\mathbf{f}_2=[1,1,0,0,1,0]$ 에서, 값이 1인 특징의 인덱스는 $\{1,2,5\}$ 입니다.
각 해시 함수에서 최소 해시 값을 계산:
$h_1(x):\left\{h_1(1)=3, h_1(2)=5, h_1(5)=4\right\} \Rightarrow \min =3$
$h_2(x):\left\{h_2(1)=5, h_2(2)=1, h_2(5)=0\right\} \Rightarrow \min =0$
$h_3(x):\left\{h_3(1)=1, h_3(2)=4, h_3(5)=0\right\} \Rightarrow \min =0$

signature: $[3,0,0]$

$\mathbf{f}_3=[0,0,1,1,0,1]$ 에서, 값이 1 인 특징의 인덱스는 $\{3,4,6\}$ 입니다.
각 해시 함수에서 최소 해시 값을 계산:
$h_1(x):\left\{h_1(3)=0, h_1(4)=2, h_1(6)=5\right\} \Rightarrow \min =0$
$h_2(x):\left\{h_2(3)=4, h_2(4)=6, h_2(6)=0\right\} \Rightarrow \min =0$
$h_3(x):\left\{h_3(3)=4, h_3(4)=1, h_3(6)=2\right\} \Rightarrow \min =1$

signature: $[0,0,1]$

결과 signature 행렬 (Signature Matrix)
Signature Matrix: $\left[\begin{array}{ll}u_1 & {[0,0,1]} \\ u_2 & {[3,0,0]} \\ u_3 & {[0,0,1]}\end{array}\right]$

2.LSH를 사용한 클러스터링
$H=3$ 차원 signature을 $b=3$ 개의 밴드로 나눕니다. 각 밴드는 $r=1$ 개의 signature 차원을 포함합니다.
(a) 밴드 구성

Band 1: 첫 번째 signature 값 $(r=1)$
Band 2: 두 번째 signature 값
Band 3: 세 번째 signature 값

3.검색 및 후보 생성

$u_1$ 을 쿼리한다고 가정합니다.
Band 1 에서 $u_1$ 과 같은 버킷에 $u_3$ 가 있습니다.
Band 2 에서는 $u_2, u_3$ 모두 후보입니다.
Band 3 에서는 $u_3$ 가 같은 버킷입니다.
결과적으로, $u_1$ 의 후보는 $\left[u_2, u_3\right]$ 가 됩니다. (이 후보는 높은 확률로 $u_1$ 와 자카드 유사도가 높을것입니다.) 필요하면 이 후보에 대해 Jaccard 유사도 또는 다른 정밀도를 계산해 최종 순위를 정합니다.

2.1.3 System

위에서 소개한 LSH(Locality-Sensitive Hashing) 기법은 시스템 구현의 복잡성을 줄이는 데 사용할 수 있습니다. MinHash LSH를 수행하면, 각 사용자 $u_i$ 는 해시 signature에 의해 생성된 버킷 ID 목록을 갖게 됩니다. 광고 캠페인에서 유사 타겟 후보를 생성하려면, 시드의 해시 signature을 조회하고, 글로벌 그래프에서 가져온 유사 사용자를 병합하여 생성할 수 있습니다.

후보 세트의 적절한 크기는 최종 유사 타겟 크기의 5배에서 10배 정도가 적당합니다.

너무 작은 후보 세트:
- 유사 타겟으로 적합할 수 있는 사용자를 누락할 위험이 있습니다.
너무 큰 후보 세트:
- 2단계(Phase II) 계산 비용이 증가합니다.

만약 그래프에서 가져온 후보 사용자의 수가 적은 경우(예: 시드가 적어서 발생), 회귀 모델(regression-based) 또는 세그먼트 근사(segment approximation-based) 방법을 사용하여 원하는 크기의 유사 타겟을 확보할 수 있습니다.

2.2 Phase II: Campaign Specific Modeling

이 단계(Phase II)에서는 캠페인별 간단한 모델을 학습하여 Phase I에서 생성된 후보 유사 타겟 사용자(candidates)를 정제(refine)합니다. 다음과 같은 작업을 수행하려고 합니다.

후보 사용자들을 캠페인별 특징 가중치로 스코어링.
상위 순위의 사용자들을 최종 유사 타겟(look-alike audience)으로 선정.

캠페인별 특징 가중치의 필요성

광고 캠페인마다 중요하게 여기는 사용자 특징이 다릅니다.
- Ex : 소매점 광고: 사용자 위치(location)를 중시.
- Ex : 보험 광고: 사용자 재정 상태(financial status)를 중시.
각 캠페인에 최적화된 가중치 행렬 A를 사용하면, 불필요한 특징을 무시하고 중요한 특징만 반영하여 ROI(Return on Investment)를 극대화할 수 있습니다

Feature 에 대한 중요도 계산 방법

가중치 행렬 $A$ : 대각 행렬로, $A_{i, j}=0(i \neq j), A_{j, j}$ 는 특징 $j$ 의 중요도를 나타냄.
특징 중요도는 시드 집합 $S$ 와 비교 집합 $U$ 를 기반으로 계산:
- 시드 집합 $S$ : 광고주가 제공.
- 비교 집합 $U$ : 여러 방식으로 구성 가능.
  - 광고를 보았지만 클릭하거나 전환하지 않은 사용자.
  - 후보 사용자 전체.
특징 $j$ 의 중요도를 계산하기 위한 비율:

p_j=\frac{\sum_{f_i \in S} f_{i, j}}{|S|}, \quad q_j=\frac{\sum_{f_i \in U} f_{i, j}}{|U|}

정보 값 (IV, Information Value)

IV는 특징의 예측력을 측정하는 방법 중 하나이며, 다음과 같이 계산:

A_{j, j}= \begin{cases}\left(p_j-q_j\right) \log \left(\frac{p_j\left(1-q_j\right)}{\left(1-p_j\right) q_j}\right), & \text { if } p_j>0.5 \\ 0, & \text { otherwise }\end{cases}

특징 $j$ 의 중요도 해석
- $p_j>0.5$ : 해당 특징이 시드 사용자에서 비교 집합 사용자보다 더 많이 나타남.
- $A_{j, j}=0$ : 시드와 비교 집합 간 차이가 크지 않음.
$p_j>0.5$ 라는 조건은 선택적 필터로, 시드 사용자에서 두드러지는 특징(positive feature)만 선택하도록 강 제합니다.

모델 투명성

높은 IV 값을 가진 상위 특징은 예측력(predictive power)이 더 강하며, 광고주에게 제공되어 모델의 투 명성을 높일 수 있습니다.
직관적 설명:
관련성 높은 특징은 시드 사용자와 다른 사용자들을 더 잘 구분할 수 있습니다.

간단한 특징 선택의 장점

비반복적(non-iterative): 효율적이며 빠르게 실행 가능.
다른 복잡한 방법(예: 로지스틱 회귀, 결정 트리)과 비교해, 희소한 사용자 특징 공간에서도 합리적인 성능 제 공.
추가적인 연산 부담 없이 특정 캠페인에 맞춘 맞춤형 유사 타겟을 생성 가능.

로지스틱 회귀의 초평면 식

로지스틱 회귀 모델의 분류 초평면(hyperplane) 식:

\sum_{i=0}^K \hat{\beta}_i x_i=C

$C$ : 상수(constant).
$x_i: i$ -번째 특징 값.
$\hat{\beta}_i$ : 해당 특징의 추정된 가중치(회귀 계수).
이 식은 표준화된 특징(standardized features)을 기반으로 정의되며, 양성/음성 라벨의 확률을 예측할 수 있음.**

특징 중요도의 해석

$x_i$ 가 이진 특징(binary features) 인 경우:
- $\hat{\beta}_i$ 는 특징 $f_{i, j}$ 의 존재/부재 여부가 로그 오즈 비(log-odd ratio)에 미치는 영향을 나타냄.
- 따라서, $\hat{\beta}_i$ 는 해당 특징의 중요도를 나타내는 값으로 해석 가능.
특징 중요도의 순위화:
- $\hat{\beta}_i$ 의 절댓값 $\left|\hat{\beta}_i\right|$ 을 기준으로 정렬하면, 각 특징의 상대적 중요도를 나타낼 수 있음.
- 즉, $\left|\hat{\beta}_i\right|$ 가 클수록 해당 특징이 분류 결정에 더 큰 영향을 미친다고 볼 수 있음.

2.2.1 스코어 계산 공식

위 논리를 바탕으로, 사용자 스코어링 방법은 다음과 같은 프레임워크에 따라 진행

s\left(f_i\right)=\sum_{j=0}^K \beta_j f_{i, j}+\sum_{g, j=0}^K \beta_{j g} f_{i, j} f_{i, g}

$\beta_j$ : 각 특징 $j$ 의 중요도를 측정하는 1차 가중치.
$\beta_{j g}$ : 특징 $j$ 와 $g$ 간 상호작용(interaction)의 중요도를 측정하는 2차 가중치.

이 식은 특징의 독립적 중요도뿐만 아니라, 특징 간 상호작용의 중요도까지 반영하는 확장된 스코어링 방법입니다.

IV 기반 스코어링

위 스코어링의 한 가지 구현은 **정보 값(IV)를 활용하는 것입니다:

s\left(f_i, c\right)=\sum_{1 \leq j \leq K} A_{j, j} f_{i, j}

$A_{j, j}$ : 캠페인 $c$ 에서 특징 $j$ 의 중요도(IV 값).
$f_{i, j}$ : 사용자 $i$ 의 특징 $j$ 값.

스코어의 목적:
- 후보 사용자 집합을 스코어링하여 순위를 매깁니다.
- 상위 사용자(Top-N)를 최종 유사 타겟으로 추천합니다.
스코어가 무한대일 수 있음:
- 스코어 식은 boundary 가 없습니다. 그러나 순위를 매기고 상위 사용자만을 추천하는 데 사용되므로, 스코어 값의 절대 크기보다는 상대적 순위가 중요합니다. (적당히 큰 값 넣어서 대체하면 된다는 의미인듯?)
스코어 정규화 (옵션):
- 스코어를 $[0,1]$ 범위로 정규화하면, 광고주가 추천 오디언스의 크기와 품질을 쉽게 제어할 수 있습니다.
- 정규화를 위해 시그모이드 함수를 사용할 수 있습니다:

s(t)=\frac{1}{1+e^{-\beta t}}

이 정규화된 스코어를 사용하면, 상위 $N$ 명의 사용자를 정렬하지 않고도 특정 임계값(threshold)을 설정 하여 선택할 수 있습니다.

2.3 System Design and Pipeline

Yahoo!의 그래프 기반 유사 타겟 시스템(graph-constraint look-alike system)은 실제 운영 환경에서 동작하며, 수천 개의 유사 타겟 오디언스 세트를 생성합니다. 이 시스템은 다음 4가지 주요 구성 요소로 이루어져 있습니다:

1. 글로벌 사용자 그래프 생성

목적: 주기적으로 사용자 간 유사성을 기반으로 글로벌 사용자 그래프를 생성.
작업 흐름:
1. 사용자 프로필 서비스에서 각 사용자의 구성된 특징(user features)을 로드.
2. 사내 LSH 패키지를 호출하여 사용자들을 다양한 버킷으로 해싱.
3. 두 사용자의 유사도가 설정된 임계값을 초과할 경우, MinHash 테이블의 r개 밴드들에 대해서 동일한 버킷에 해싱될 가능성이 높음.
4. 모든 사용자를 처리한 후, MapReduce 작업으로 버킷 ID별로 사용자들을 그룹화.
5. 동일한 버킷에 속하는 사용자들을 함께 저장하여 효율적인 사용자 쿼리를 지원.

2. 후보 사용자 수집

목적: 시드 사용자 집합을 기반으로 후보 사용자 집합을 생성.
작업 흐름:
1. 시스템은 입력으로 시드 사용자 ID 목록을 받음.
2. 시드 사용자들의 특징을 해싱하여 이들이 속하는 버킷을 식별.
3. 해당 버킷에 속한 사용자들을 모두 병합하여 후보 사용자 집합을 생성.
4. 시드 확장 과정이 끝나면, 사용자 프로필 서비스에서 후보 사용자 정보를 쿼리하고, 사용자 ID 및 특징 데이터를 HDFS에 저장.

3. 특징 중요도 계산

목적: 각 Feature의 중요도를 계산하여 캠페인별 최적화에 활용.
작업 흐름:
1. 글로벌 사용자 수와 시드 사용자 수를 각 Feature별로 읽어들임.
2. 각 Feature의 중요도를 계산.
3. 계산된 결과를 HDFS에 저장.
효율성 개선: 글로벌 Feature 분포는 모든 캠페인에서 공유 가능하므로, Feature 중요도 학습을 매우 효율적으로 수행할 수 있음.

4. 사용자 스코어링 및 추천

목적: 후보 사용자들을 스코어링하고 상위 사용자들을 캠페인 타겟으로 추천.
작업 흐름:
1. HDFS에서 두 개의 데이터 세트를 읽어들임:
  - 상위 K Feature 목록 및 해당 중요도 점수.
  - 후보 사용자와 그들의 Feature 데이터.
2. 모든 후보 사용자에 대해 캠페인별 Feature 중요도를 기준으로 스코어링.
3. 모든 후보 사용자를 순위화하여 상위 NNN 사용자 ID를 선정.
4. 선정된 사용자 ID를 사용자 프로필 서비스로 전송하여 캠페인 타겟팅 정보를 업데이트.

이 시스템은 글로벌 사용자 그래프 생성 → 후보 사용자 수집 → Feature 중요도 계산 → 사용자 스코어링 및 추천의 4단계를 거쳐 유사 타겟 오디언스를 효율적으로 생성합니다. 각 단계는 HDFS와 MapReduce를 활용해 대규모 데이터를 처리하며, 캠페인 맞춤형 타겟팅을 지원합니다.

3 Evaluation Methodology

실험 목적

광고 캠페인 목표: 앱 설치 캠페인에서 광고주는 새로운 사용자들이 앱을 설치하도록 유도하면서, 목표 설치당 비용(Cost-Per-Install, CPI)을 충족하는 것입니다.
평가 초점:
- 유사 타겟 시스템(look-alike system)이 특정 앱 광고에 대해 얼마나 정확하게 타겟팅할 수 있는지를 측정.
- 광고 선택 알고리즘(어떤 광고를 어떤 사용자에게 노출할지)은 논문 범위 밖.

평가 방법

오프라인 Back-Play 테스트:
- 실제 온라인 광고 캠페인은 비용이 높으므로, 오프라인 데이터 기반으로 성능 평가.
- Back-Play 테스트: 과거 데이터를 사용해 유사 타겟 시스템의 성능을 시뮬레이션.

시드 사용자 구성 방법

광고주가 시드 사용자 목록을 구성하는 방법은 캠페인 목표에 따라 다양:
1. 최근 인앱 구매 사용자를 시드로 사용하여, 잠재적으로 인앱 구매 가능성이 높은 사용자 탐색.
2. 기존 설치 사용자를 시드로 사용하여, 잠재적인 앱 설치 가능 사용자 탐색.
본 실험에서 시뮬레이션한 시나리오:
- 기존 설치 사용자를 시드로 사용하여, 유사 타겟 시스템을 통해 앱 설치 가능성이 높은 사용자를 탐색.

실험 단계

시드 사용자 수집:
- 특정 날짜 $t_0$ 를 기준으로 $t_0$ 에서 $t_1$ 까지의 기간(예: 1 개월) 동안 앱 설치자를 수집하여 시드 사용자로 설 정.
유사 타겟 확장:
- 유사 타겟 시스템을 사용해 시드 사용자를 확장하여, ${ }^{* *}$ 크기 $n^{* *}$ 의 유사 타겟 오디언스를 생성.
성능 계산:
- 테스트 기간 $\left(t_1, t_2\right]$ (예: 2주) 동안 추천된 오디언스의 앱 설치율(app installation rate)을 계산.
비교 실험:
- 유사 타겟 시스템의 성능 비교:
- 각 시스템에 대해 오디언스 크기 $n$ 을 다르게 설정하며 성능을 비교.

3.1 데이터와 평가 지표

사용자 Feature

데이터 수집:
- 앱 개발자가 Yahoo! 제공 SDK를 사용할 경우, 앱 설치와 사용 데이터를 추적 및 기록.
- 이 데이터를 기반으로 사용자 Feature 벡터(user feature vector)를 생성.
사용자 Feature 구성:
- 앱 설치: 사용자가 설치한 앱.
- 앱 카테고리: 사용자가 선호하는 앱 카테고리(예: 스포츠, 어드벤처 게임).
- 앱 사용 활동: 사용 빈도 및 활동 데이터.
- 앱 메타 정보: 앱에 대한 추가 데이터.
글로벌 그래프:
- 테스트 기간 직전의 사용자 프로필 스냅샷을 기반으로 구축.
- 10억 명 이상의 모바일 사용자 포함.
- 동일한 사용자 Feature이 단순 유사성 기반 방법, 로지스틱 회귀, 그리고 세그먼트 근사 방법에서도 사용됨.
  - 세그먼트 근사 방법 비교: 사용자 앱 관심 카테고리(예: 스포츠, 어드벤처 게임)를 세그먼트로 활용.

시드 데이터

시드 사용자:
- Yahoo! 광고 플랫폼에서 월간 전환자(converters)가 10,000명 이상인 100개 앱 샘플링.
- 각 앱에 대해, 2015년 5월 앱 설치자를 시드 사용자로 설정.
테스트 데이터:
- 테스트 대상: 2015년 6월 첫 2주간의 활성 사용자.
- 양성 예시(positive examples): 테스트 앱의 신규 설치자.
- 음성 예시(negative examples): 앱을 설치하지 않은 사용자.

성능 지표

설치율(Installation Rate, IR):
추천된 오디언스 $(\mathrm{A})$ 중 테스트 기간 동안 대상 앱 $(\mathrm{P})$ 을 설치한 비율:

I R(P, A)=\frac{|I|}{|A|}

여기서:

$I$ : 추천된 오디언스 $A$ 에서 신규 설치자의 집합.
$|A|$ : 추천된 고유 사용자 수.
설치율 계산 방식:
- 일반적인 전환율 계산에서는 노출 수(impressions)가 분모가 됨.
- 그러나 여기서는 추천된 고유 사용자 수를 분모로 사용.
- 이유: 광고 노출 시간 결정(ad serving time decision) 없이, 추천된 오디언스가 앱 설치 가능성이 높은 지를 평가.

4 Conclusion

설치율(Installation Rate, IR) 비교 방법

추천 오디언스 크기(n)를 다양하게 설정하며 각 모델의 설치율(IR)을 계산.
모델별 스코어링:
- Graph-Constraint Model (GCL):
  - 후보 사용자(Phase I 결과)는 시드와의 유사도가 사전에 설정된 임계값보다 높은 사용자들로 구성.
  - 스코어를 기반으로 상위 n명의 사용자를 선정.
- Logistic Regression (LR):
  - 후보 사용자 집합에서 상위 n명의 스코어링된 사용자를 선정.
- Simple Similarity-Based Method (JaccardSim):
  - 시드와 후보 사용자의 쌍별 유사도를 계산하지 않기 위해 후보 집합에서 무작위로 n명을 샘플링.
- Segment Approximation Method:
  - 후보 사용자 간 순위가 없으므로, 후보 집합에서 무작위로 n명을 샘플링.

주요 결과 및 분석

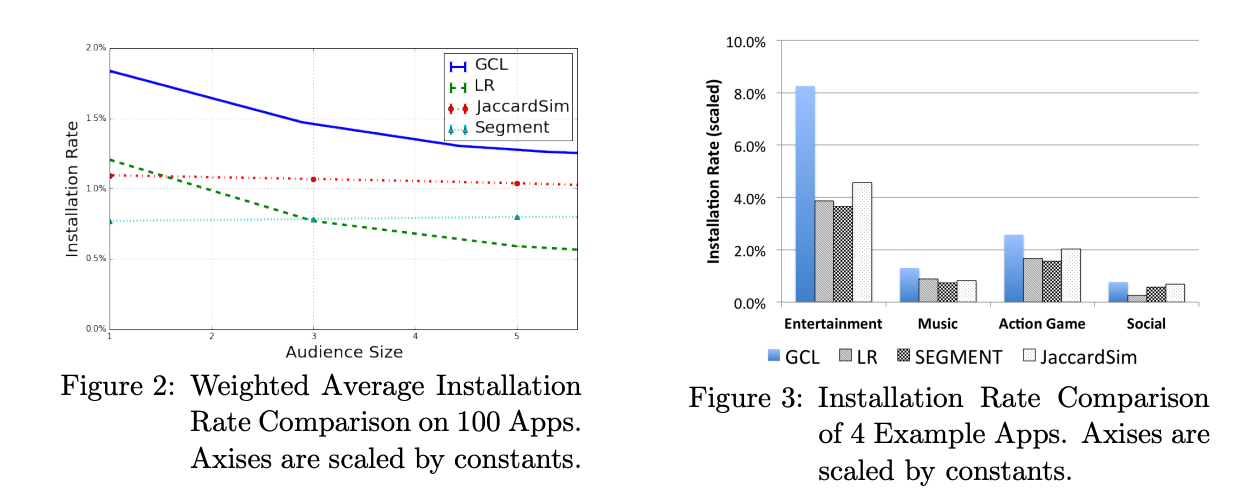
Figure 2: 모든 모델의 설치율 비교

결과 요약:
- GCL 모델:
  - 모든 모델 중 가장 우수한 성능.
  - 추천 오디언스 크기가 작을수록 성능 격차가 큼.
  - 작은 오디언스 크기에서는 JaccardSim 대비 50% 이상의 설치율 개선.
  - 오디언스 크기가 증가할수록 설치율은 점진적으로 감소.
- JaccardSim 모델:
  - 오디언스 크기에 관계없이 성능이 비교적 안정적.
  - 시드와 유사한 사용자의 평균 설치율을 반영.
- LR 모델:
  - 오디언스 크기가 작을 때 JaccardSim 및 Segment 모델보다 성능이 우수.
  - 오디언스 크기가 커질수록 성능이 급격히 하락.
  - 이유: 사용자 특징의 희소성으로 인해 특정 앱의 특징이 중요한 역할을 하지 못할 때, 무작위 사용자 선택과 비슷한 결과를 초래.
- Segment 모델:
  - 특정 오디언스 크기에서 성능이 안정적이나 GCL 및 LR보다 낮음.

Figure 3: 앱 카테고리별 설치율 비교

결과 요약:
- 모든 모델에서 엔터테인먼트 및 액션 게임 앱의 성능이 소셜 앱보다 우수.
- 소셜 앱:
  - 새로운 소셜 앱을 설치하는 빈도가 낮음.
  - 사용자들이 이미 사용 중인 소셜 앱을 안정적으로 유지하는 경향이 있음.
  - 친구들과의 연결이 중요한 소셜 앱에서는 예측 가능한 특징 신호(signal)가 부족.
- 엔터테인먼트/액션 게임 앱:
  - 사용자들이 새로운 엔터테인먼트 소스를 탐색하거나, 기존 게임에서 난관에 부딪힐 때 새로운 앱을 설치하는 경향이 강함.
  - 이러한 앱들은 관련 사용자 신호가 많아, 유사 타겟 모델이 더 나은 예측을 할 수 있음.
    주요 결론

GCL 모델의 우수성:
- 오디언스 크기가 작을 때 특히 뛰어난 성능.
- 시드와 높은 유사성을 가진 사용자 그룹을 우선적으로 타겟팅.
LR 모델의 한계:
- 소규모 오디언스에서는 유의미한 특징을 활용해 성능이 좋지만, 오디언스가 커질수록 노이즈와 희소성의 영향을 크게 받음.
앱 카테고리별 성능 차이:
- 소셜 앱은 관련 특징 신호가 부족하여 타겟팅 성능이 낮음.
- 엔터테인먼트 및 액션 게임 앱에서는 더 강력한 타겟팅 성능을 보임.

GCL 모델은 다양한 크기의 오디언스에서 우수한 성능을 보이며, 특히 소규모 오디언스에서 높은 설치율을 달성.
사용자 특징의 희소성은 LR 모델의 성능에 부정적인 영향을 미침.
앱 카테고리에 따라 모델 성능이 다르게 나타나며, 엔터테인먼트와 액션 게임 앱은 타겟팅 예측이 더 효과적임

4.1 Summary

본 논문에서는 Yahoo!의 대규모 유사 타겟 확장 시스템을 소개했습니다.
시스템 특징:
- 유사 사용자 쿼리 시간은 **서브-선형(sub-linear)으로 동작.
- 핵심 모델: 사용자 간 쌍별 유사성(pairwise user-2-user similarity)을 기반으로 한 그래프 마이닝(graph mining) 및 머신러닝 기법.

Yahoo!의 유사 타겟 시스템 성능

시스템 운영 현황:
- Yahoo!의 유사 타겟 시스템은 실제 프로덕션 환경에서 동작.
- 프로덕션 파이프라인의 처리 능력:
  - 3000개 이상의 캠페인 스코어링.
  - 100개의 노드에서 약 3000개의 매퍼를 활용.
  - 30억 명 이상의 사용자 데이터와 수백만 개의 특징을 약 4시간 내에 처리.
실제 캠페인 성과:
- 전환율(Conversion Rate): 기존 타겟팅 옵션(예: 인구통계학적 타겟팅 또는 관심사 기반 타겟팅) 대비 최대 40% 개선.
- 전환당 비용(Cost-Per-Conversion): 최대 50% 절감.

개인적인 생각

의외로 모델링쪽에서는 별다른게 없어서 놀람. (아마 실시간 서빙이 부담되어서 그런듯?)
spark 에 구현되어있는게 있어서 쓸 수 있을지도?
시드를 확장하는 개념으로 LSH 를 쓰는것 같은데.. 이게 어느정도는 이해가 가는데, Interaction 을 효과적으로 잡아내지는 못할 것 같아서 결국에는 모델 기반 추정이 더 좋을 것 같다는 생각이 듦..

gorany

3년차 데이터 분석가

다음 포스트