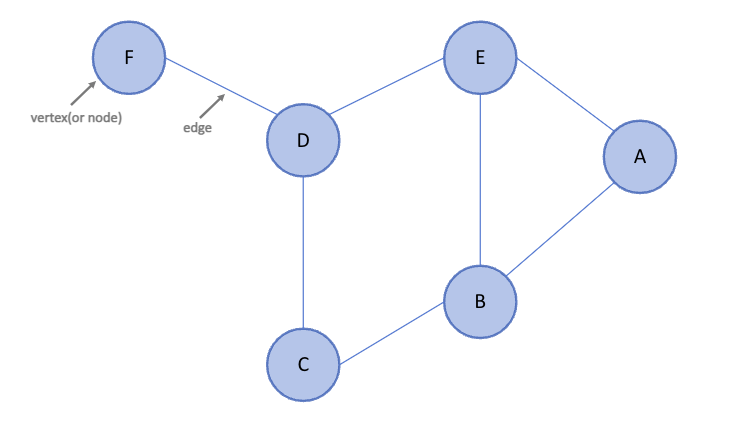
그래프(Graph)란?
그래프(Graph)는 연결되어있는 원소 간의 관계를 표현한 자료구조이다.
연결할 객체를 나타내는 정점(Node or Vertex)과 객체를 연결하는 간선(Edge)의 집합으로 구성된다.
그래프는 G=(V, E)처럼 정의하는데, V는 정점의 집합, E는 간선들의 집합을 의미한다.
무방향 그래프에서 정점 Vi와 Vj를 연결하는 간선을 (Vi,Vj)로 표현하며, 방향 그래프에서는 정점 Vi와 Vj를 연결하는 간선을 <Vi,Vj>로 표현한다.
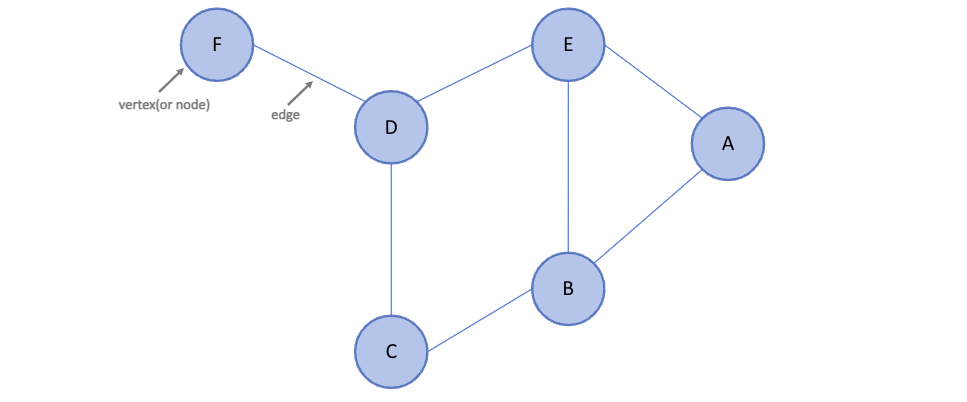
- 무방향 그래프
V(G1) = { A, B, C, D, E, F }
E(G1) = { (A,B), (A,E), (B,C), (B,E), (C,D), (D,E), (D,F) }- 방향 그래프
V(G2) = { A, B, C, D, E, F }
E(G2) = { <A,B>, <A,E>, <B,E>, <C,B>, <D,C>, <D,F>, <E,D> }
*(Vi,Vj) 와 (Vj,Vi)는 같은 간선을 나타내지만, <Vi,Vj> 와 <Vj,Vi>는 서로 다른 간선이다
그래프의 특징
그래프는 여러가지 특징을 가진다. 다만 하나의 그래프가 모든 특징을 가지는 것이 아니라 특징을 가짐에 따라 그래프의 종류도 나뉘어진다.
-
무방향성(Undirectionality): 그래프의 간선은 방향성이 없을 수 있으며, 양쪽 방향으로 모두 이동할 수 있다. 무뱡향의 의미는 방향을 강제하는 일방통행이 없다는 의미로 생각할 수 있으며, 이러한 그래프를 무방향 그래프(undirected graph)라고 부른다.
-
방향성(Directionality): 그래프의 간선은 방향성이 있을 수 있으며, 한쪽 방향으로만 이동할 수 있다.
이러한 그래프를 방향 그래프(directed graph) 또는 유향 그래프(digraph)라고 부른다. -
가중치(Weight): 그래프의 간선에는 가중치를 부여할 수 있다.
가중치를 부여한 그래프를 가중치 그래프(weighted graph)라고 부르며, 보통은 거리, 비용, 우선순위 등을 나타내는데 사용된다. -
연결성(Connectivity): 그래프에서 노드와 노드 사이에 경로가 존재하면, 두 노드는 연결되었다고 말한다.
그래프가 연결되어 있는 경우 연결 그래프(connected graph)라고 부르며, 그렇지 않은 경우 비연결 그래프(disconnected graph)라고 부른다. -
사이클(Cycle): 그래프에서 한 노드에서 시작하여 경로를 따라가면서 자기 자신으로 돌아오는 경로를 사이클이라고 부른다. 사이클이 없는 그래프를 비순환 그래프(acyclic graph)라고 부르며, 사이클이 있는 그래프를 순환 그래프(cyclic graph)라고 부른다.
-
차수(Degree): 그래프에서 한 노드에 인접한 간선의 수를 차수라고 부른다.
무방향 그래프에서는 노드의 차수가 연결된 노드의 수와 같으며, 방향 그래프에서는 들어오는 노드의 수(진입차수)와 나가는 노드의 수(진출차수)로 구분된다.
그래프의 용도 및 응용 분야
-
경로 탐색 및 최적화
지도에서의 최단 경로 찾기(예: 구글 맵의 길 찾기), 내비게이션 시스템, 물류 경로 최적화 등에서 그래프를 사용해 최단 경로나 최적 경로를 계산한다.
대표적인 예로는, 다익스트라 알고리즘, 벨만-포드 알고리즘 등있다. -
웹 페이지 순위 결정
검색 엔진에서 웹 페이지의 중요도를 평가하기 위해 그래프 이론을 사용힌다.
대표적인 알고리즘으로 구글의 페이지랭크(PageRank)가 있으며, 이는 웹 페이지를 노드로, 링크를 엣지로 간주해 중요도를 계산한다. -
게임 개발 및 인공지능
게임 맵에서의 경로 찾기, 캐릭터의 AI 결정 트리, 상태 전이 다이어그램 등을 그래프를 통해 모델링한다.
이와 같은 그래프 기반 모델은 게임 캐릭터의 움직임이나 의사결정을 최적화하는 데 사용된다.
그래프 관련 용어
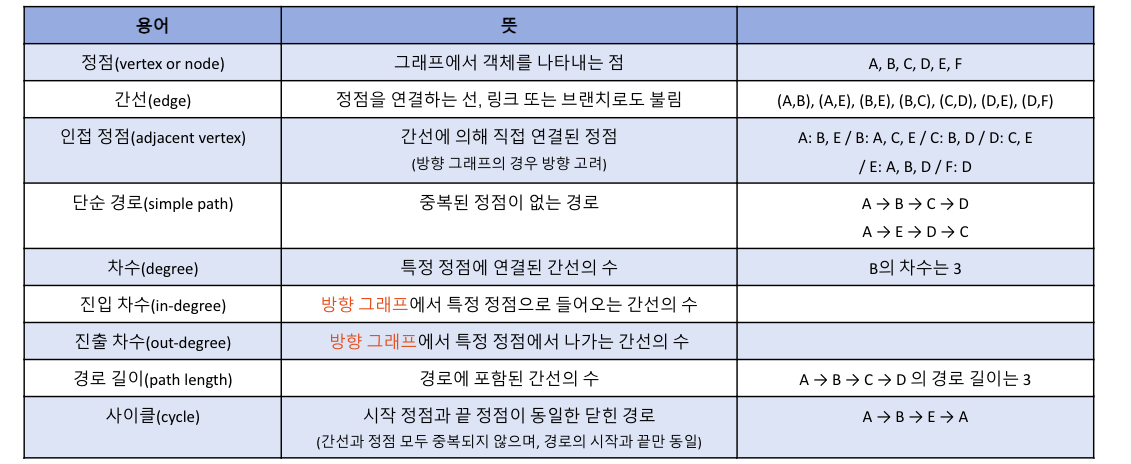
그래프 유형
무방향 그래프(Undirected Graph)
두 정점을 연결하는 간선에 방향이 없는 그래프이며, 노드 사이의 관계는 양방향이다.
방향 그래프(Directed Graph)
두 정점을 연결하는 간선에 방향이 있는 그래프이며, 노드 사이의 관계는 단방향이다.
가중치 그래프(Weighted Graph)
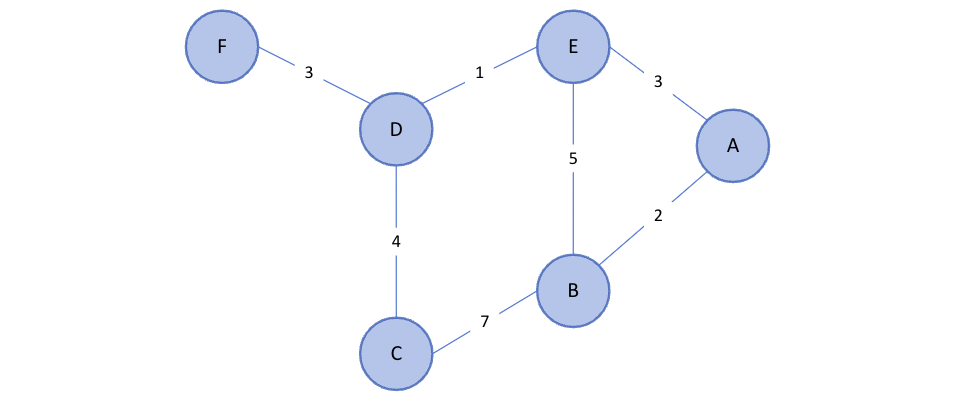간선에 가중치가 있는 그래프이며, 가중치는 간선의 비용, 거리, 시간 등을 나타낸다.
가중치 그래프에서는 모든 간선에 가중치가 있는 것이 일반적이지만, 반드시 모든 간선이 가중치를 가질 필요는 없다. 상황에 따라서는 특정 간선에만 가중치를 부여할 수도 있다.
완전 그래프(Complete Graph)
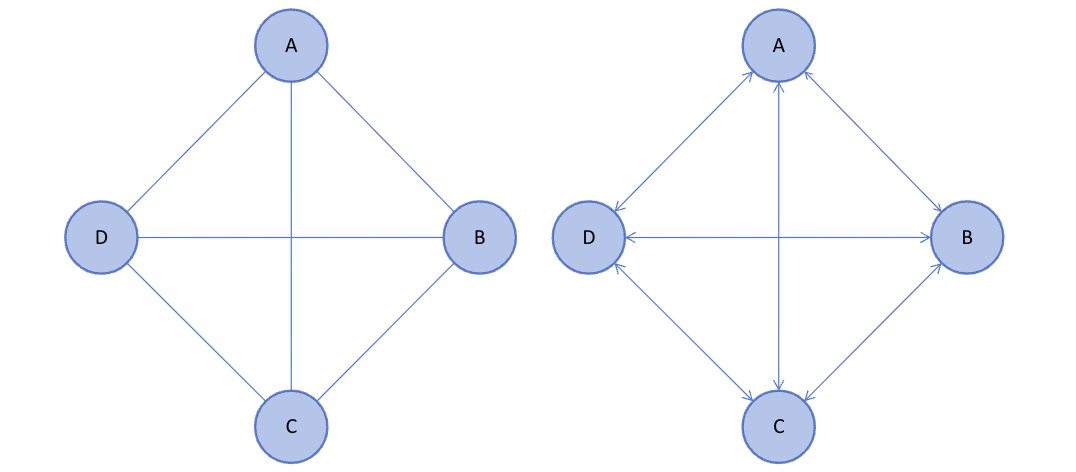모든 정점이 간선으로 연결된 그래프이다.
무방향 완전 그래프의 정점의 수가 n이라면, 전체 간선의 수는 n(n-1)/2가 된다.
방향 완전 그래프의 정점의 수가 m이라면, 전체 간선의 수는 m(m-1)이 된다.
순환 그래프(Cyclic Graph)
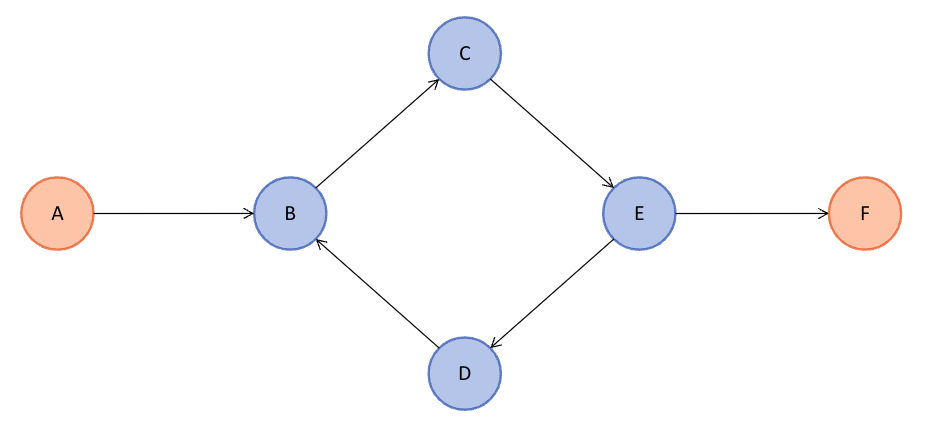그래프 내에 사이클이 존재하는 그래프이다. 즉, 어떤 정점에서 출발해 간선을 따라 이동하여 다시 출발점으로 돌아오는 경로가 하나 이상 존재하는 그래프이다.
비순환 그래프(Acyclic Graph)
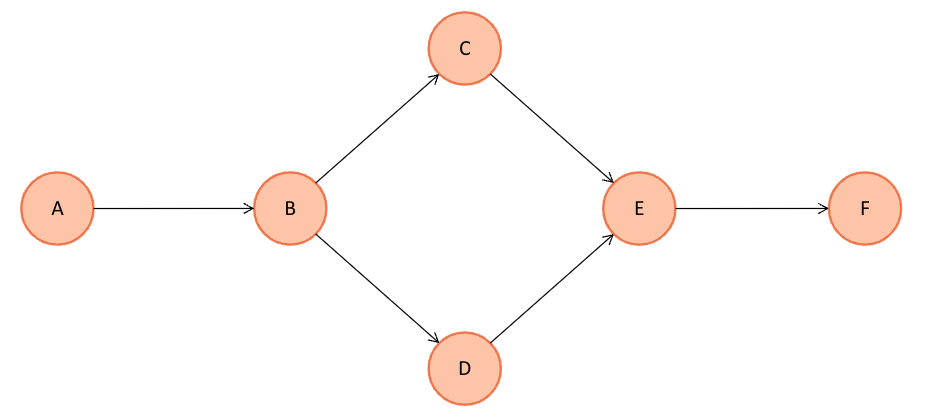그래프 내에 사이클이 존재하지 않는 그래프이다. 즉, 어떤 정점에서 출발해 다시 그 정점으로 돌아오는 경로가 없는 그래프이다.
그래프 구현 방법
컴퓨터에서 그래프를 구현하는 방법에는 배열(Array)을 사용하는 방법과 연결리스트(Linked List)를 사용하는 방법이 있다.
인접 행렬(Adjacency Matrix)
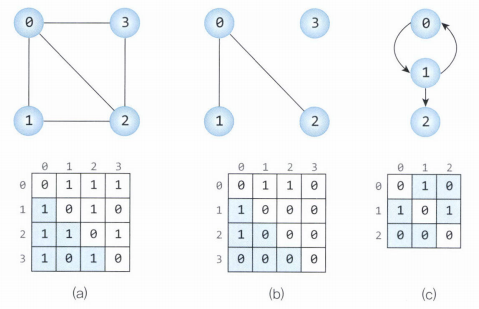그래프의 정점을 2차원 배열로 만든 것이다.
정점의 개수가 n이라면 n*n 형태의 2차원 배열이 인접 행렬로 사용된다.
인접 행렬에서 행과 열은 정점을 의미하며, 각각의 원소들은 정점 간의 간선을 나타낸다.
무방향 그래프는 (a),(b)에서 볼 수 있듯이 인접 행렬이 대칭적 구조를 가진다.
(두 개의 정점에서 간선이 동시에 연결되어 있기 때문)
가중치 그래프의 경우 행렬에서 0과 1이 아니라 각 간선의 가중치 값이 저장된다.
(이 경우 가중치가 0인 것과 간선이 없는 것이 구별돼야 함)
- 장점
- 2차원 배열에 모든 정점들의 간선 정보가 있기 때문에, 두 정점을 연결하는 간선을 조회할 때 O(1) 시간복잡도로 가능하다.
- 정점(i)의 차수를 구할 때는 다음과 같이 인접행렬의 i번째 행의 값을 모두 더하면 되므로 O(n)의 시간 복잡도를 가진다.
- 단점
- 간선의 수와 무관하게 항상 n² 크기의 2차원 배열이 필요하므로 메모리 공간이 낭비된다.
- 그래프의 모든 간선의 수를 알아내려면 인접 행렬 전체를 확인해야 하므로 O(n²)의 시간이 소요된다.
# 인접 행렬을 이용하여 무방향 그래프 구현
class AdjMatGraph:
MAX_VTXS = 256 # 최대 정점의 개수를 256으로 정의
def __init__(self):
# 생성자: 그래프 초기화
self.size = 0 # 현재 그래프에 있는 정점의 개수를 저장
self.vertices = [''] * self.MAX_VTXS # 정점들을 저장할 리스트 (정점 이름 저장)
self.adjMat = [[0] * self.MAX_VTXS for _ in range(self.MAX_VTXS)] # 인접 행렬을 0으로 초기화
def get_vertex(self, i):
# 정점의 이름을 반환하는 함수
return self.vertices[i]
def get_edge(self, i, j):
# 두 정점 간의 간선이 있는지(1: 연결됨, 0: 연결되지 않음) 반환
return self.adjMat[i][j]
def set_edge(self, i, j, val):
# 두 정점 간의 간선을 설정하는 함수 (값을 1로 설정하면 간선이 추가됨)
self.adjMat[i][j] = val
def reset(self):
# 그래프를 초기화하는 함수 (모든 간선을 0으로 설정하고, 정점의 개수를 0으로 리셋)
for i in range(self.MAX_VTXS):
for j in range(self.MAX_VTXS):
self.set_edge(i, j, 0) # 모든 간선을 끊음
self.size = 0 # 정점의 개수를 0으로 초기화
def insert_vertex(self, name):
# 정점을 그래프에 삽입하는 함수
if self.is_full():
# 정점의 개수가 최대치에 도달하면 오류 메시지를 출력
print("Graph vertex full error")
return
# 정점을 vertices 리스트에 추가하고 size 값을 증가시킴
self.vertices[self.size] = name
self.size += 1
def insert_edge(self, u, v):
# 두 정점 간에 간선을 삽입하는 함수 (무방향 그래프이므로 양방향 모두 설정)
self.set_edge(u, v, 1) # u에서 v로 간선을 추가
self.set_edge(v, u, 1) # v에서 u로 간선을 추가
def display(self):
# 그래프의 인접 행렬 및 정점 정보를 출력하는 함수
print(f"vertex size : {self.size}")
print(" ", end="")
# 정점 이름 출력
for i in range(self.size):
print(self.get_vertex(i), end=" ")
print()
# 인접 행렬 출력
for i in range(self.size):
print(f"{self.get_vertex(i)} : ", end="")
for j in range(self.size):
print(self.get_edge(i, j), end=" ")
print()
def is_empty(self):
# 그래프가 비어 있는지 확인하는 함수
return self.size == 0
def is_full(self):
# 그래프가 꽉 찼는지 확인하는 함수 (MAX_VTXS와 size 비교)
return self.size >= self.MAX_VTXS
# 테스트
graph = AdjMatGraph()
# 정점 삽입 (A, B, C, D)
graph.insert_vertex('A') # 0
graph.insert_vertex('B') # 1
graph.insert_vertex('C') # 2
graph.insert_vertex('D') # 3
# 간선 삽입
graph.insert_edge(0, 1) # A -> B
graph.insert_edge(0, 2) # A -> C
graph.insert_edge(0, 3) # A -> D
graph.insert_edge(2, 3) # C -> D
# 그래프 출력
graph.display()<결과>
vertex size : 4
A B C D
A : 0 1 1 1
B : 1 0 0 0
C : 1 0 0 1
D : 1 0 1 0 인접 리스트(Adjacency List)
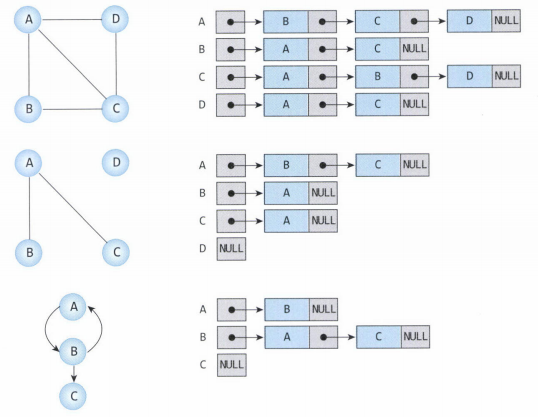
그래프의 각 정점에 인접한 정점들을 연결리스트(Linked List)로 표현하는 방법이다.
즉, 정점의 개수만큼 인접리스트가 존재하며, 각각의 인접리스트에는 인접한 정점 정보가 저장된다.
무방향 그래프의 경우, 간선이 추가되면 각각의 정점의 인접리스트에 반대편 정점의 노드를 추가해야한다.
- 장점
- 존재하는 간선만 관리하면 되므로 메모리 사용 측면에서 보다 효율적이다.
- 그래프의 모든 간선의 수를 알아내려면 각 정점의 헤더 노드부터 모든 인접리스트를 탐색해야 하므로 O(n+e)의 시간이 소요된다.
- 단점
- 두 정점을 연결하는 간선을 조회하거나 정점의 차수를 알기 위해서는 정점의 인접 리스트를 탐색해야 하므로 정점의 차수만큼의 시간이 필요하다. (O(degree(v)))
- 구현이 비교적 어렵다.
# 인접 리스트를 이용하여 무방향 그래프 구현
class Node:
def __init__(self, _id, _link=None):
self.id = _id # 정점의 ID
self.link = _link # 다음 노드에 대한 링크
def get_id(self):
return self.id
def set_id(self, _id):
self.id = _id
def get_link(self):
return self.link
def set_link(self, _link):
self.link = _link
class AdjListGraph:
MAX_VTXS = 256 # 최대 정점 개수
def __init__(self):
self.size = 0 # 정점의 개수
self.vertices = [''] * self.MAX_VTXS # 정점 이름을 저장할 리스트
self.adj_list = [None] * self.MAX_VTXS # 인접 리스트를 저장할 리스트
def get_vertex(self, i):
return self.vertices[i]
def reset(self):
# 그래프 초기화: 모든 인접 리스트와 정점 수를 초기화
for i in range(self.size):
if self.adj_list[i] is not None:
self._delete_list(self.adj_list[i])
self.size = 0
def _delete_list(self, node):
# 인접 리스트를 재귀적으로 삭제하는 함수
while node is not None:
next_node = node.get_link()
del node
node = next_node
def insert_vertex(self, name):
if self.is_full():
print("Graph vertex full error")
return
self.vertices[self.size] = name
self.adj_list[self.size] = None
self.size += 1
def insert_edge(self, u, v):
# 정점 u와 v 간에 간선 추가 (무방향 그래프)
self.adj_list[u] = Node(v, self.adj_list[u])
self.adj_list[v] = Node(u, self.adj_list[v])
def display(self):
# 그래프의 인접 리스트와 정점 정보를 출력
print(f"vertex size : {self.size}")
for i in range(self.size):
print(f"{self.get_vertex(i)} : ", end="")
node = self.adj_list[i]
while node is not None:
print(self.get_vertex(node.get_id()), end=" ")
node = node.get_link()
print()
def adjacent(self, v):
return self.adj_list[v]
def is_empty(self):
return self.size == 0
def is_full(self):
return self.size >= self.MAX_VTXS
# 테스트
graph = AdjListGraph()
# 정점 삽입 (A, B, C, D)
graph.insert_vertex('A') # 0
graph.insert_vertex('B') # 1
graph.insert_vertex('C') # 2
graph.insert_vertex('D') # 3
# 간선 삽입
graph.insert_edge(0, 1) # A -> B
graph.insert_edge(0, 2) # A -> C
graph.insert_edge(0, 3) # A -> D
graph.insert_edge(2, 3) # C -> D
# 그래프 출력
graph.display()<결과>
vertex size: 4
A : D C B
B : A
C : D A
D : C A 인접 행렬 vs 인접 리스트
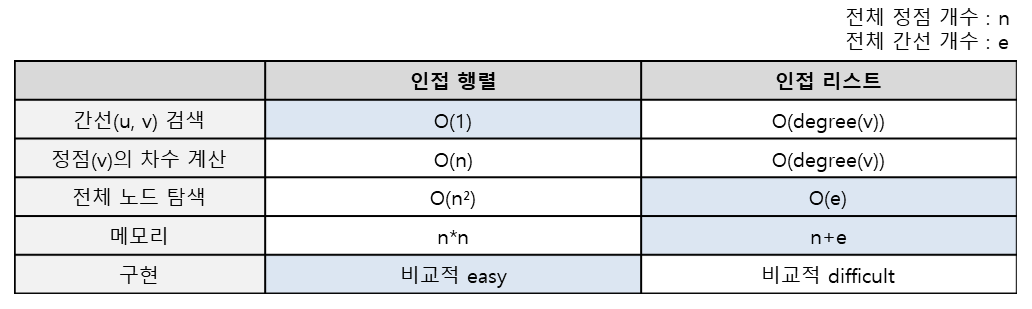만약 10억 개의 노드가 있고 각 노드가 2개씩의 간선만 있는 상황에 인접 행렬로 구현한 그래프에서는 한 정점의 차수를 구할때 10억 번의 연산을 수행할 것이고, 인접리스트로 구현한 그래프에서는 2번의 연산만 수행하면 된다.
정점의 개수에 비해 간선의 개수가 매우 적은 희소 그래프(sparse graph)에서는 인접리스트가 유리할 수 있고, 모든 정점간에 간선이 존재하는 완전 그래프(complete graph)에서는 인접행렬이 유리할 수 있다.
그래프에서 주로 어떤 연산이 수행되는지도 매우 중요하게 고려되어야 하는 요소이며, 상황에 따라 최선의 방법을 선택하여 그래프를 구현해야한다.
그래프 탐색 알고리즘
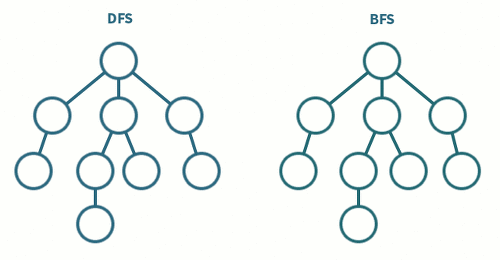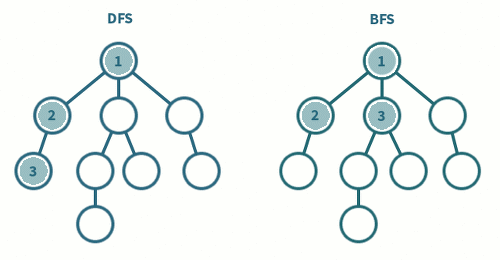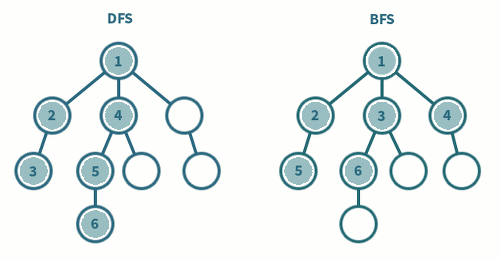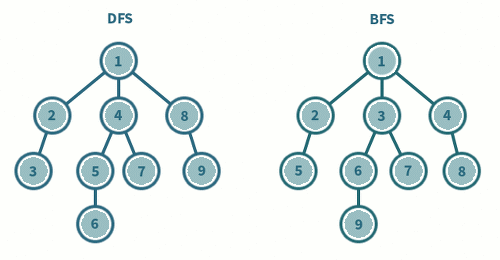
- 깊이 우선 탐색(Depth-First Search, DFS)
- 특정 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 끝까지 탐색하는 방법을 뜻한다.
- 갈 수 있는 만큼 최대한 깊이 가고, 더 이상 갈 곳이 없다면 이전 정점으로 돌아가는 방식으로 그래프를 순회한다.
- 주로 재귀 호출과 스택을 사용해서 구현한다.
- 너비 우선 탐색(Breadth-First Search,BFS)
- 특정 노드에서 시작하여 인접한 노드를 먼저 탐색해 나가는 방법을 뜻한다.
- 시작 정점을 방문한 후 시작 정점에서 인접한 모든 정점을 방문한다.
인접한 정점을 방문한 뒤, 다시 해당 정점의 인접한 정점을 방문하며 그래프를 순회한다. - 주로 큐와 반복문을 사용해서 구현한다.
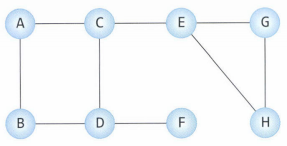해당 그래프를 인접 행렬과 인접 리스트로 생성한 후, 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)의 예제 코드를 Python으로 구현하였다.
인접 행렬을 이용한 DFS 구현
class SearchAdjMatGraph(AdjMatGraph):
def __init__(self):
super().__init__()
self.visited = [False] * self.MAX_VTXS # 방문 배열 초기화
def reset_visited(self):
# 모든 정점의 방문 기록을 False로 초기화
self.visited = [False] * self.size
def dfs(self, v):
# 정점 v에서 DFS 탐색 시작
self.reset_visited()
self.dfs_recur(v)
print() # DFS 출력 후 줄 바꿈
def dfs_recur(self, v):
# 재귀적으로 DFS 탐색
self.visited[v] = True
print(self.get_vertex(v), end=" ")
for n in range(self.size):
if self.get_edge(v, n) == 1 and not self.visited[n]:
self.dfs_recur(n)
def main():
graph = SearchAdjMatGraph()
# 정점 추가
vertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
for vertex in vertices:
graph.insert_vertex(vertex)
# 간선 추가
edges = [
(0, 1), (0, 2), (1, 3), (2, 3), (2, 4),
(3, 5), (4, 6), (4, 7), (6, 7)
]
for u, v in edges:
graph.insert_edge(u, v)
print("== Display Graph ==")
graph.display()
print("-DFS => ", end="")
graph.dfs(0)
main()<결과>
== Display Graph ==
vertex size : 8
A B C D E F G H
A : 0 1 1 0 0 0 0 0
B : 1 0 0 1 0 0 0 0
C : 1 0 0 1 1 0 0 0
D : 0 1 1 0 0 1 0 0
E : 0 0 1 0 0 0 1 1
F : 0 0 0 1 0 0 0 0
G : 0 0 0 0 1 0 0 1
H : 0 0 0 0 1 0 1 0
-DFS => A B D C E G H F 인접 리스트를 이용한 DFS 구현
class SearchAdjListGraph(AdjListGraph):
def __init__(self):
super().__init__()
self.visited = [False] * self.MAX_VTXS # 방문 기록을 위한 배열
def reset_visited(self):
# 모든 정점의 방문 기록을 False로 초기화
self.visited = [False] * self.size
def dfs(self, v):
# 정점 v에서 DFS 탐색 시작
self.reset_visited()
self.dfs_recur(v)
print() # DFS 탐색 후 줄 바꿈
def dfs_recur(self, v):
# 재귀적으로 DFS 탐색
self.visited[v] = True
print(self.get_vertex(v), end=" ")
node = self.adj_list[v]
while node is not None:
if not self.visited[node.get_id()]:
self.dfs_recur(node.get_id())
node = node.get_link()
def main():
graph = SearchAdjListGraph()
# 정점 삽입
vertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
for vertex in vertices:
graph.insert_vertex(vertex)
# 간선 삽입
edges = [
(0, 1), (0, 2), (0, 3), (2, 3),
(2, 4), (3, 5), (4, 6), (4, 7), (6, 7)
]
for u, v in edges:
graph.insert_edge(u, v)
print("== Display Graph ==")
graph.display()
print("-DFS => ", end="")
graph.dfs(0)
main()<결과>
== Display Graph ==
vertex size : 8
A : D C B
B : A
C : E D A
D : F C A
E : H G C
F : D
G : H E
H : G E
-DFS => A D F C E H G B 인접 행렬과 인접 리스트의 방문 순서의 차이
- 인접 행렬로 구현한 경우, 행렬의 인덱스 순서대로 각 정점의 인접한 정점들을 탐색하므로, 정점 번호가 작은 것부터 방문하는 경향이 있다.
- 인접 리스트로 구현한 경우, 인접한 정점들이 저장된 순서에 따라 탐색하므로, 저장된 순서에 따라 방문 순서가 달라질 수 있다. 만약 인접 정접들이 정렬되지 않은 상태라면 방문 순서는 뒤섞일 수 있다.
요약하자면, 인접 행렬은 정점의 인덱스 순서를 따르는 반면, 인접 리스트는 저장된 순서에 의존한다. 따라서 그래프의 구조나 탐색 결과(방문한 노드)는 동일하지만, 정점 방문 순서는 사용한 자료구조에 따라 달라질 수 있다.
인접 행렬을 이용한 BFS 구현
from collections import deque
class SearchAdjMatGraph(AdjMatGraph):
def __init__(self):
super().__init__()
self.visited = [False] * self.MAX_VTXS # 방문 배열 초기화
def reset_visited(self):
# 모든 정점의 방문 기록을 False로 초기화
self.visited = [False] * self.size
def bfs(self, v):
# 정점 v에서 BFS 탐색 시작
self.reset_visited()
queue = deque([v])
self.visited[v] = True
print(self.get_vertex(v), end=" ")
while queue:
v = queue.popleft()
for n in range(self.size):
if self.get_edge(v, n) == 1 and not self.visited[n]:
print(self.get_vertex(n), end=" ")
self.visited[n] = True
queue.append(n)
print() # BFS 출력 후 줄 바꿈
def main():
graph = SearchAdjMatGraph()
# 정점 추가
vertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
for vertex in vertices:
graph.insert_vertex(vertex)
# 간선 추가
edges = [
(0, 1), (0, 2), (1, 3), (2, 3), (2, 4),
(3, 5), (4, 6), (4, 7), (6, 7)
]
for u, v in edges:
graph.insert_edge(u, v)
print("== Display Graph ==")
graph.display()
print("-BFS => ", end="")
graph.bfs(0)
main()<결과>
== Display Graph ==
vertex size : 8
A B C D E F G H
A : 0 1 1 0 0 0 0 0
B : 1 0 0 1 0 0 0 0
C : 1 0 0 1 1 0 0 0
D : 0 1 1 0 0 1 0 0
E : 0 0 1 0 0 0 1 1
F : 0 0 0 1 0 0 0 0
G : 0 0 0 0 1 0 0 1
H : 0 0 0 0 1 0 1 0
-BFS => A B C D E F G H
인접 리스트를 이용한 BFS 구현
from collections import deque
class SearchAdjListGraph(AdjListGraph):
def __init__(self):
super().__init__()
self.visited = [False] * self.MAX_VTXS # 방문 기록을 위한 배열
def reset_visited(self):
# 모든 정점의 방문 기록을 False로 초기화
self.visited = [False] * self.size
def bfs(self, v):
# 정점 v에서 BFS 탐색 시작
self.reset_visited()
queue = deque([v])
self.visited[v] = True
print(self.get_vertex(v), end=" ")
while queue:
v = queue.popleft()
node = self.adj_list[v]
while node is not None:
n_id = node.get_id() # 인접 노드의 정점 ID
if not self.visited[n_id]:
print(self.get_vertex(n_id), end=" ")
self.visited[n_id] = True
queue.append(n_id)
node = node.get_link()
print() # BFS 탐색 후 줄 바꿈
def main():
graph = SearchAdjListGraph()
# 정점 삽입
vertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
for vertex in vertices:
graph.insert_vertex(vertex)
# 간선 삽입
edges = [
(0, 1), (0, 2), (0, 3), (2, 3),
(2, 4), (3, 5), (4, 6), (4, 7), (6, 7)
]
for u, v in edges:
graph.insert_edge(u, v)
print("== Display Graph ==")
graph.display()
print("-BFS => ", end="")
graph.bfs(0)
main()<결과>
== Display Graph ==
vertex size : 8
A : D C B
B : A
C : E D A
D : F C A
E : H G C
F : D
G : H E
H : G E
-BFS => A D C B F E H G *DFS는 경로 탐색, 사이클 검출, 백트래킹 문제 해결 등에 사용되며, 인접 행렬은 밀집 그래프에, 인접 리스트는 희소 그래프에 적합하다.
*BFS는 최단 경로 탐색, 레벨 순서 탐색 등에서 사용되며, 인접 행렬은 밀집 그래프에, 인접 리스트는 희소 그래프에 효율적이다.
*이러한 특성에 따라 문제의 요구사항과 그래프의 구조에 맞게 DFS와 BFS를 선택하고, 적절한 자료 구조(인접 행렬 또는 인접 리스트)를 결정하는 것이 중요하다.
[참고 자료]
https://80000coding.oopy.io/125156cf-79bb-48da-82ae-1f2ee7896bb8
https://leejinseop.tistory.com/43
https://velog.io/@kwontae1313/%ED%8A%B8%EB%A6%AC%EC%99%80-%EA%B7%B8%EB%9E%98%ED%94%84%EC%97%90-%EB%8C%80%ED%95%B4-%EC%95%8C%EC%95%84%EB%B3%B4%EC%9E%90
https://6mini.github.io/computer%20science/2021/12/02/graph/
https://suyeon96.tistory.com/32
