인공지능을 위한 선형대수 1
에드위드 - 인공지능을 위한 선형대수 by 주재걸 교수님
선형 시스템 및 선형 변환
행렬 곱
- AB과 BA는 같지않음. 교환법칙(commutative) 성립 안됨
- 행렬의 곱셈 : A x B의 경우 A의 col과 B의 row 사이즈 같아야함.
- 분배법칙 성립 A(B+C) = AB + AC
- transpose시 순서가 바뀌는 성질
- 역행렬의 경우 순서가 바뀌는 성질
선형 방정식(Linear Equation)
- a1x1+a2x2+...+anxn = b <=> a^T+x=b(두 방정식은 같은것)
- 소문자는 벡터, 대문자는 행렬
- Linear System : 연립방정식의 집합
항등행렬
- 정사각형 행렬이면서, 대각선은 1이고 나머지는 0인 행렬.
Inx=x -> 어떤 항등 행렬과 곱해져도 자기자신
역행렬
- 기본 행렬에 역행렬을 곱할 때 항상 항등행렬
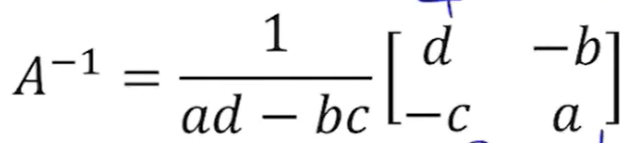
- ad=bc의 경우 역행렬 존재하지 않음

몸무게, 키, 흡연 유무 등의 특성들을 가진 사람들의 수명을 표현한 방정식을 통해서 어떤 것이 얼마나 큰 가중치를 갖는지 계산 가능.
역행렬이 없는 행렬
- no solution or infinitely many solutions(변수와 방정식 간의 관계를 통하여)
- 비율이 똑같을 때 (ad=bc)
머신러닝에 적용
=> regulization을 통해 만족하는 모든 해 중에서 risk를 최소화 하는 coefficient(가중치)를 안정한 솔루션으로 판단.
(해를 만족하는 선형 방정식 내에서 linear 전체 부분에서 학습데이터에서 동일한 성능을 내도 위치가 어디냐에 따라 테스트의 경우에 다른 성능을 낼 수 있으므로 그것이 최소화 되는 해를 구하게 됨)
선형 결합
- p개의 벡터에 각 상수배를 해서 더해주는 것. 가능한 선형 결합들을 다 모아 늘리면 = 평면 (span), 3차원의 부분집합
선형결합의 가중치를 잘 조합하여 원하는 벡터를 만들 수 있느냐(3개의 재료 벡터를 이용해서 원하는 span에 포함하는 선형 결합으로 표현할 수 있으냐)

-벡터들의 sum of outer products를 사용하여 완벽하진않지만 근사하게 엄청 커다란 행렬들을 표현 할 수 있음.(아래의 경우는 완벽하게 같음)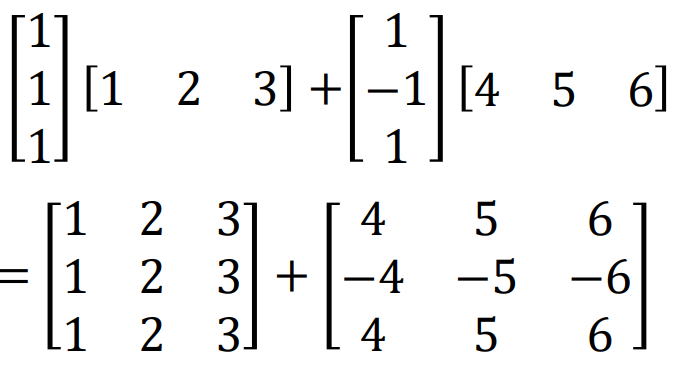
선형독립
- a1x1+a2x2+a3x3 = b 를 만족하는 x들의 해가 unique한 경우
- 해가 여러개가 존재할 경우 선형의존이 됨.(linealy dependent) 여러개의 평행 사변형을 그릴 수 있음. 두개로 만든 span에 나머지 재료 벡터가 포함되는지 아닌지로 독립인지 의존인지 알 수 있음.
선형변환
- T(cu + dv ) = cT(u) +dT(v)
- 뉴럴 넷에서 풀리 커넥티드 레이어의 기본적인 변환
- 모눈 종이를 평행사변형의 꼴로 만들어주는 것(non linear의 경우 구겨짐)
- 이것을 통해 bias를 해결
