데이터 분석 29일차
1. 모집단 (Population)
✅ 모집단은 연구나 분석을 위한 전체 집단을 의미합니다.
✅ 모집단을 완벽하게 파악하는 것은 현실적으로 어려운 경우가 많다.
2. 표본 (Sample)
✅ 표본은 모집단에서 일부를 뽑아낸 작은 집단입니다.
✅ 표본을 통해 모집단의 특성을 추정하는 것이 일반적인 방법입니다.
✅ 표본은 모집단을 대표할 수 있는 집합이어야 하며, 일반적으로 무작위 추출을 통해 얻습니다.
표본은 모집단을 대표하는 작은 집단입니다.
import numpy as np
import matplotlib.pyplot as plt
# 모집단 생성 (예: 국가의 모든 성인의 키 데이터)
population = np.random.normal(170, 10, 1000)
# 표본 추출
sample = np.random.choice(population, 100)
plt.hist(population, bins=50, alpha=0.5, label='population', color='blue')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='red')
plt.legend()
plt.title('population and sample distribution')
plt.show()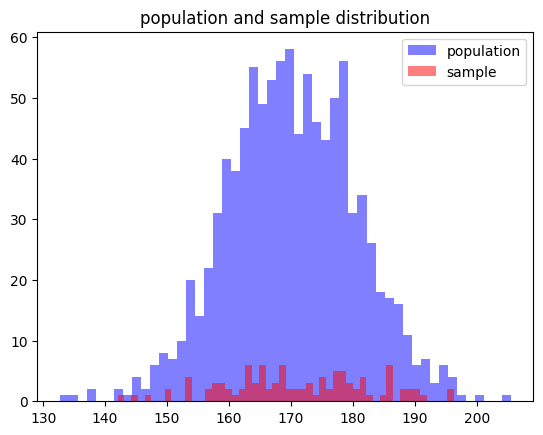
3. 표본오차 (Sampling Error)
✅ 표본오차는 표본이 모집단을 정확히 대표하지 못할 때 발생하는 오차입니다.
✅ 이는 표본의 특성에 따라 발생하며, 모집단과 표본 간의 차이로 인한 오차입니다.
✅ 표본오차는 우연적인 차이로, 표본의 크기나 선택 방법에 따라 달라질 수 있습니다. 표본의 크기가 커질수록 표본오차는 줄어듭니다.
4. 표본구간 (Confidence Interval)
✅ 표본구간은 모집단의 특성을 추정할 때, 추정값이 포함될 범위를 나타냅니다.
- 예를 들어, 평균값에 대한 추정에서 95% 신뢰구간은 "모집단 평균이 이 구간 내에 있을 확률이 95%"라는 의미입니다. 표본구간은 표본오차를 반영하여, 모집단의 실제 값이 포함될 가능성이 높은 범위를 제공합니다.
✅ 표본구간은 모집단의 특성값이 포함될 가능성이 높은 범위를 제공합니다.
import scipy.stats as stats
# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)
# 95% 신뢰구간 계산 -- 모집단 평균이 이 구간에 들어 온다.
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))
print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")
1. 정규분포 (Normal Distribution)
✅ 정규분포는 가장 흔한 분포로, 데이터가 평균을 중심으로 대칭적으로 분포하는 형태이다.
✅ 종 모양의 그래프를 가진다.
✅ 정규분포는 평균과 표준편차를 기준으로 데이터가 어떻게 분포하는지 나타냅니다.
# 정규분포 생성
normal_dist = np.random.normal(170, 10, 1000)
# 히스토그램으로 시각화
plt.hist(normal_dist, bins=30, density=True, alpha=0.6, color='g')
# 정규분포 곡선 추가
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, 170, 10)
plt.plot(x, p, 'k', linewidth=2)
plt.title('normal distribution histogram')
plt.show()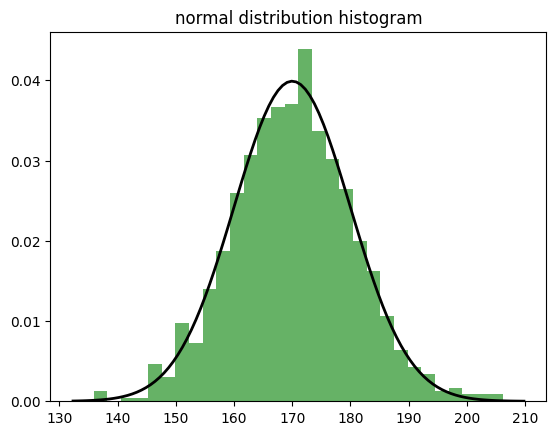
2. 롱 테일 분포
✅ 롱 테일 분포는 소수의 큰 값과 많은 작은 값이 존재하는 분포입니다.
- 예를 들어, 부유한 사람이 전체 자산의 대부분을 소유하는 형태로, 많은 값이 적고 일부 값이 매우 큰 특징을 가집니다.
✅ 롱 테일 분포는 소수의 큰 값과 많은 작은 값들이 존재하는 비대칭적인 분포입니다.
# 긴 꼬리 분포 생성 (예: 소득 데이터)
long_tail = np.random.exponential(1, 1000)
# 히스토그램으로 시각화
plt.hist(long_tail, bins=30, density=True, alpha=0.6, color='b')
plt.title('long tail distribution histogram')
plt.show()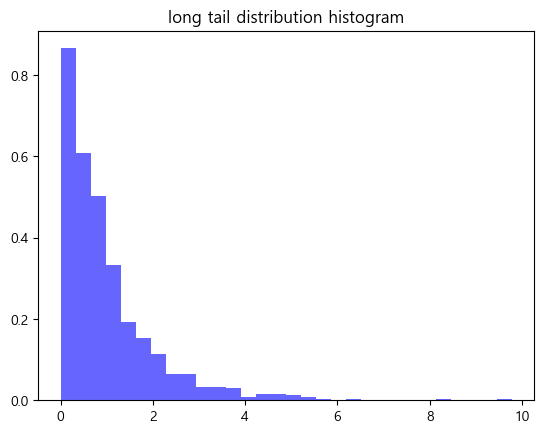
3. 스튜던트 t-분포 (Student's t-Distribution)
✅ 스튜던트 t-분포는 표본 크기가 작은 경우 사용됩니다.
✅ 정규분포와 비슷하지만, 꼬리가 두껍고 길어 표본의 불확실성을 반영합니다.
✅ 표본 크기가 커지면 정규분포와 비슷해지며, 평균을 추정하는 데 유용하다.
# 스튜던트 t 분포 생성
t_dist = np.random.standard_t(df=10, size=1000)
# 히스토그램으로 시각화
plt.hist(t_dist, bins=30, density=True, alpha=0.6, color='r')
# 스튜던트 t 분포 곡선 추가
x = np.linspace(-4, 4, 100)
p = stats.t.pdf(x, df=10) ## df는 자유도
plt.plot(x, p, 'k', linewidth=2)
plt.title('student t distribution histogram')
plt.show()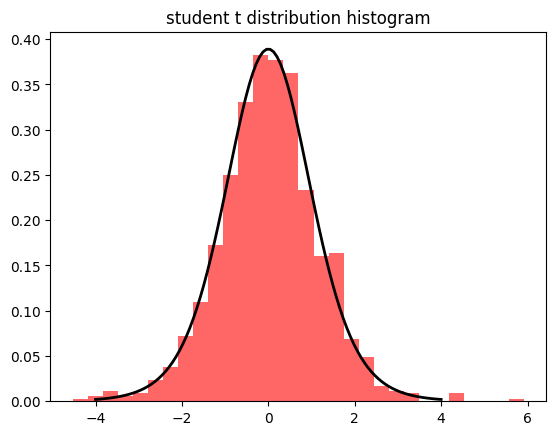
4. 카이 제곱 분포 (Chi-Square Distribution)
✅ 카이 제곱 분포는 주로 적합도 검정과 독립성 검정에서 사용됩니다.
✅ 이 분포는 모든 값이 양수이며, 자유도에 따라 모양이 달라집니다.
✅ 자유도가 커지면 정규분포에 가까워집니다.
✅ 카이 제곱 분포는 주로 데이터의 분포나 두 변수 간 관계를 검정하는 데 사용됩니다.
# 카이제곱분포 생성
chi2_dist = np.random.chisquare(df=2, size=1000)
# 히스토그램으로 시각화
plt.hist(chi2_dist, bins=30, density=True, alpha=0.6, color='m')
# 카이제곱분포 곡선 추가
x = np.linspace(0, 10, 100)
p = stats.chi2.pdf(x, df=2)
plt.plot(x, p, 'k', linewidth=2)
plt.title('카이제곱 분포 히스토그램')
plt.show()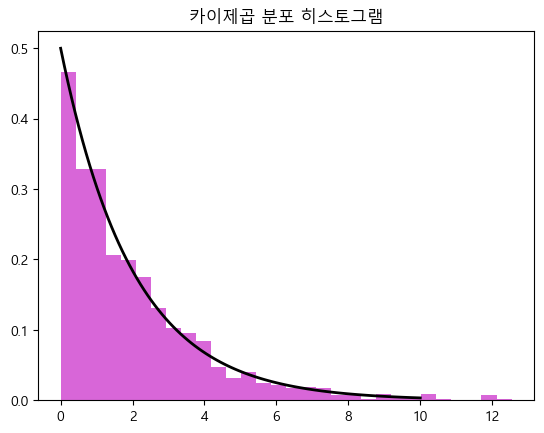
5. 이항 분포 (Binomial Distribution)
✅ 이항 분포는 두 가지 가능한 결과(예: 성공/실패)가 있는 실험에서 성공 횟수를 구할 때 사용됩니다.
- 예를 들어, 동전을 던졌을 때 앞면이 나오는 횟수를 나타낼 때 사용됩니다.
✅ 이항 분포는 주어진 횟수에서 특정 이벤트가 발생하는 횟수를 나타냅니다.
✅ 이벤트가 독립적이고, 각 이벤트의 확률이 일정한 조건에서 사용됩니다.
# 이항분포 생성 (예: 동전 던지기 10번 중 앞면이 나오는 횟수)
binom_dist = np.random.binomial(n=10, p=0.5, size=1000)
## n= 몇번 던질지, p= 한번던질때 확율
# 히스토그램으로 시각화
plt.hist(binom_dist, bins=10, density=True, alpha=0.6, color='y')
plt.title('이항 분포 히스토그램')
plt.show()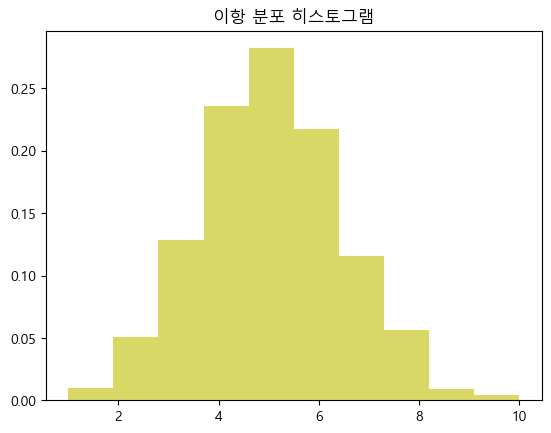
6. 푸아송 분포 (Poisson Distribution)
✅ 푸아송 분포는 주어진 시간 동안 일어나는 사건의 수를 나타냅니다.
✅ 주로 드문 사건이 발생하는 경우
- 예를 들어 고객이 매장에 도착하는 빈도를 모델링할 때 사용됩니다.
✅ 사건이 독립적이고, 일정 평균 발생률을 가진 경우에 적용됩니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 푸아송 분포 파라미터 설정
lambda_value = 4 # 평균 발생률
x = np.arange(0, 15) # 사건 발생 횟수 범위
# 푸아송 분포 확률 질량 함수 계산
poisson_pmf = poisson.pmf(x, lambda_value)
# 그래프 그리기
plt.figure(figsize=(10, 6))
plt.bar(x, poisson_pmf, alpha=0.6, color='b', label=f'Poisson PMF (lambda={lambda_value})')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.legend()
plt.grid(True)
plt.show()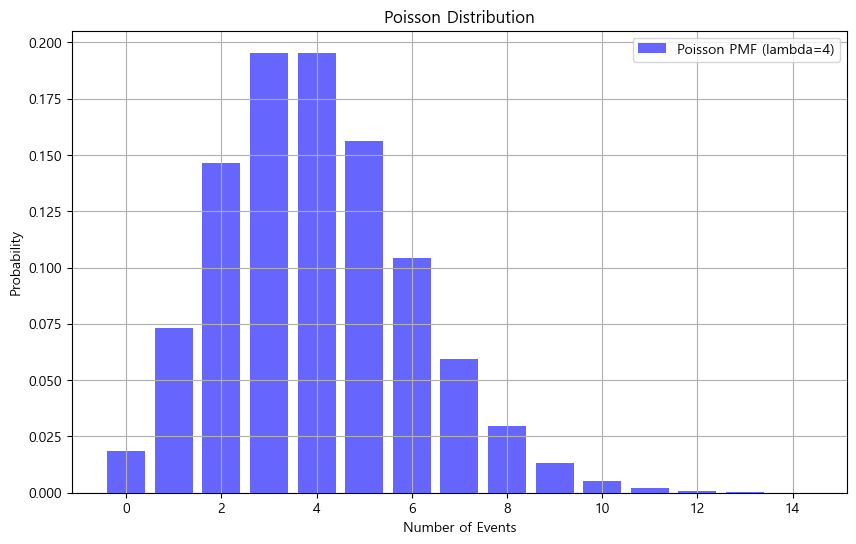
📌 코드는 위에것 부터 실행하기~!
📝 정리
-
정규분포: 데이터가 평균을 중심으로 대칭적으로 퍼지며, 데이터의 대부분이 평균 근처에 집중되어 있습니다.
-
긴 꼬리 분포: 소수의 큰 값과 많은 작은 값들이 존재하는 비대칭적인 분포이다.
-
스튜던트 t-분포: 표본 크기가 작을 때 사용되며, 표본의 불확실성을 반영하여 더 넓고 두꺼운 꼬리를 가집니다.
-
카이 제곱 분포: 주로 적합도 검정이나 독립성 검정에서 사용되며, 모든 값이 양수이고 자유도에 따라 모양이 달라집니다.
-
이항 분포: 두 가지 가능한 결과가 있는 실험에서 성공 횟수를 계산하는 분포로, 각 이벤트의 확률이 일정합니다.
-
푸아송 분포: 일정 시간 동안 드문 사건의 발생 횟수를 모델링하며, 사건들이 독립적이고 일정한 평균 발생률을 가집니다.
