알고리즘강의 05. 복습

이 글은 블로그주인장이 여태 공부했던 알고리즘 독학 및 강의들의 내용을 정리하는 포스팅입니다.

정렬(2)

면접에서 물어보는 정렬이나 응용된 정렬

병합(Merge)

• 배열의 앞부분과 뒷부분의 두 그룹으로 나누어 각각 정렬한 후 병합하는 작업을 반복하는 알고리즘
• 시간복잡도: O(N)

[1,2,3,5] # 정렬된 리스트 A
[4,6,7,8] # 정렬된 리스트 B
[] # 두 집합을 합칠 빈 리스트 C

1단계 : 
[1, 2, 3, 5]
     ↓
[4, 6, 7, 8]  1과 4를 비교
1 < 4 이므로 1을 C 에 넣습니다.
C:[1]

2단계 : 
[1, 2, 3, 5]
     ↓
[4, 6, 7, 8] 2와 4를 비교
2 < 4 이므로 2를 C 에 넣습니다.
C:[1, 2]

3단계 : 
[1, 2, 3, 5]
     ↓
[4, 6, 7, 8] 3과 4를 비교
3 < 4 이므로 3을 C 에 넣습니다.
C:[1, 2, 3]

이런 식으로 동작함

#파이썬 소스코드
def merge(array1, array2):
    result = []
    array1_index = 0
    array2_index = 0
    while array1_index < len(array1) and array2_index < len(array2):
        if array1[array1_index] < array2[array2_index]:
            result.append(array1[array1_index])
            array1_index += 1
        else:
            result.append(array2[array2_index])
            array2_index += 1

    if array1_index == len(array1):
        while array2_index < len(array2):
            result.append(array2[array2_index])
            array2_index += 1

    if array2_index == len(array2):
        while array1_index < len(array1):
            result.append(array1[array1_index])
            array1_index += 1

    return result

//c 소스코드
void merge(int list[], int left, int mid, int right){
  int i, j, k, l;
  i = left;
  j = mid+1;
  k = left;

  /* 분할 정렬된 list의 합병 */
  while(i<=mid && j<=right){
    if(list[i]<=list[j])
      sorted[k++] = list[i++];
    else
      sorted[k++] = list[j++];
  }

  // 남아 있는 값들을 일괄 복사
  if(i>mid){
    for(l=j; l<=right; l++)
      sorted[k++] = list[l];
  }
  // 남아 있는 값들을 일괄 복사
  else{
    for(l=i; l<=mid; l++)
      sorted[k++] = list[l];
  }

  // 배열 sorted[](임시 배열)의 리스트를 배열 list[]로 재복사
  for(l=left; l<=right; l++){
    list[l] = sorted[l];
  }
}

https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

여기에 분할 정복의 개념을 적용하면

병합 정렬(Merge Sort)

• MergeSort(0, N) = Merge(MergeSort(0, N/2) + MergeSort(N/2, N))
• 즉, 0부터 N까지 정렬한 걸 보기 위해서는
  0부터 N/2 까지 정렬한 것과 N/2부터 N까지 정렬한 걸 합치면 된다. 라는 개념
• 시간복잡도: O(Nlog(N))

# python 소스코드
def merge_sort(array):
    if len(array) <= 1:
        return array
    mid = len(array) // 2
    left_array = array[:mid] #왼쪽 배열 생성
    right_array = array[mid:] #오른쪽 배열 생성
    return merge(merge_sort(left_array), merge_sort(right_array))

// c 소스코드
void merge_sort(int list[], int left, int right){
  int mid;

  if(left<right){
    mid = (left+right)/2 // 중간 위치를 계산하여 리스트를 균등 분할 -분할(Divide)
    merge_sort(list, left, mid); // 앞쪽 부분 리스트 정렬 -정복(Conquer)
    merge_sort(list, mid+1, right); // 뒤쪽 부분 리스트 정렬 -정복(Conquer)
    merge(list, left, mid, right); // 정렬된 2개의 부분 배열을 합병하는 과정 -결합(Combine)
  }
}

퀵정렬(Quick Sort)

• 피벗을 기준으로 큰 값과 작은 값을 서로 교체하는 하는 알고리즘
  
• 왼->오, 오->왼 으로 순회하며 피벗 기준으로 큰 값과 작은 값을 교체함
  
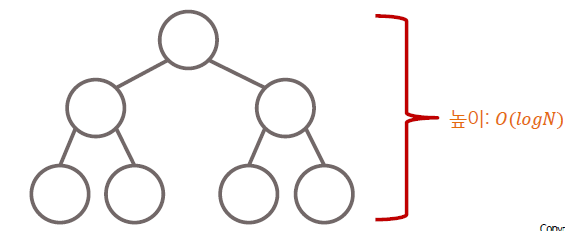
• 원소를 절반씩 나눌 때 𝑙𝑜𝑔𝑁의 시간 복잡도가 나오는 대표적인 예시는 완전 이진 트리

#파이썬 소스코드
def quick_sort(arr):
    if len(arr)<=1: #리스트 길이가 1인 경우 대비
        return arr

    pivot = arr[0] #피벗 첫번째 원소로 셋팅
    tail = arr[1:] #피벗을 제외한 리스트

    left_side=[x for x in tail if x<=pivot] #분할된 왼쪽 ==> 피벗값보다 작은 원소들로만 리스트 생성
    right_side=[x for x in tail if x>pivot] #분할된 오른쪽 ==> 피벗값보다 큰 원소들로만 리스트 생성

    return quick_sort(left_side)+[pivot]+quick_sort(right_side)

// c/c++ 소스코드
void quickSort(int* arr, int start, int end) {
	if (start >= end) return; //원소가 1개인 경우
	int pivot = start; //피벗은 첫 번째 원소
	int left = start + 1;
	int right = end;
	while (left <= right) {
		//피벗보다 큰 데이터를 찾을 때까지 반복
		while (left <= end && arr[left] <= arr[pivot]) left++;
		// 피벗보다 작은 데이터를 찾을 때까지 반복
		while (right > start && arr[right] >= arr[pivot]) right--;
		// 엇갈렸다면 작은 데이터와 피벗을 교체
		if (left > right) swap(arr[pivot], arr[right]);
		// 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
		else swap(arr[left], arr[right]);
	}
	// 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
	quickSort(arr, start, right - 1);
	quickSort(arr, right + 1, end);
}

계수정렬(Counting Sort)

• 크기를 기준으로 데이터의 개수를 세는 정렬 알고리즘
• 시간복잡도: O(N)

# 파이썬 코드
#모든 범위를 포함하는 리스트선언(모든 값은 0으로 초기화)
cnt=[0]*(max(array)+1)

for i in range(len(array)):
    cnt[array[i]]+=1 #카운트 리스트에 인덱스==arr값 1씩 증가
for i in range(len(cnt)):
    for j in range(cnt[i]):
        print(i,end=' ') # 등장 횟수 만큼 출력

// c/c++ 소스코드
int cnt[MAX_VALUE + 1];

int main(void) {
    for (int i = 0; i < n; i++) {
        cnt[arr[i]] += 1; // 각 데이터에 해당하는 인덱스의 값 증가
    }
    for (int i = 0; i <= MAX_VALUE; i++) { // 배열에 기록된 정렬 정보 확인
        for (int j = 0; j < cnt[i]; j++) {
            cout << i << ' '; // 띄어쓰기를 기준으로 등장한 횟수만큼 인덱스 출력
        }
    }
}

참고

• 학부생 시절 자료구조 강의
• 알고보면 알기 쉬운 알기쉬운 알고리즘 -스파르타 코딩클럽
• 이것이 코딩테스트다 with 파이썬 - 나동빈
• 소스코드
  https://github.com/BOLTB0X/Sparta-Algorithm/tree/main/week_3
  https://github.com/BOLTB0X/CodingTest_Book/tree/main/06Sort