Loop, I/O 병렬화

Chapter 10

I/O 병렬화

1. Input

input 1

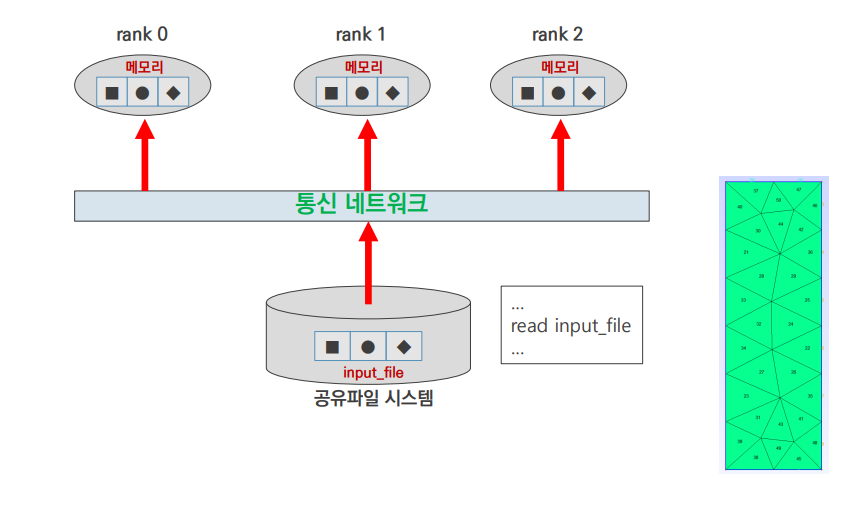
• 모든 rank가 input file을 읽어들임
• 하나의 큰 mesh data를 모든 rank가 접근
• rank가 많다면 I/O 부하 발생

input 2

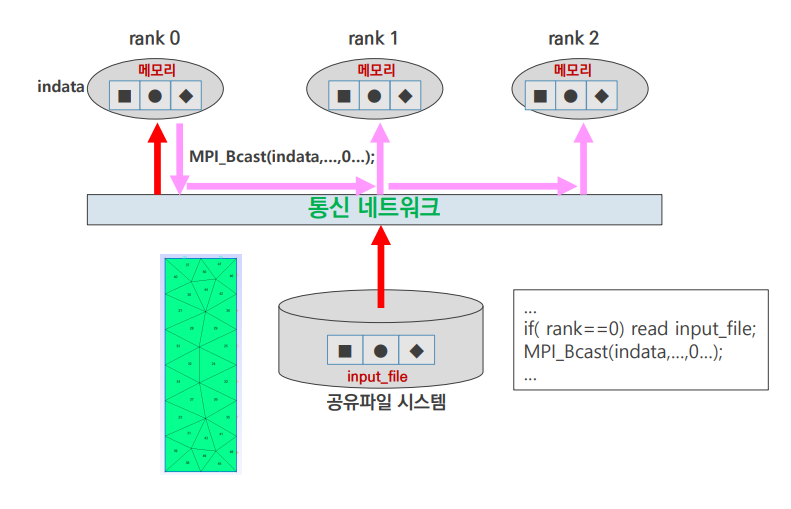
• 하나의 rank가 input data를 읽어들임
• 모든 rank로 broadcast

input 3

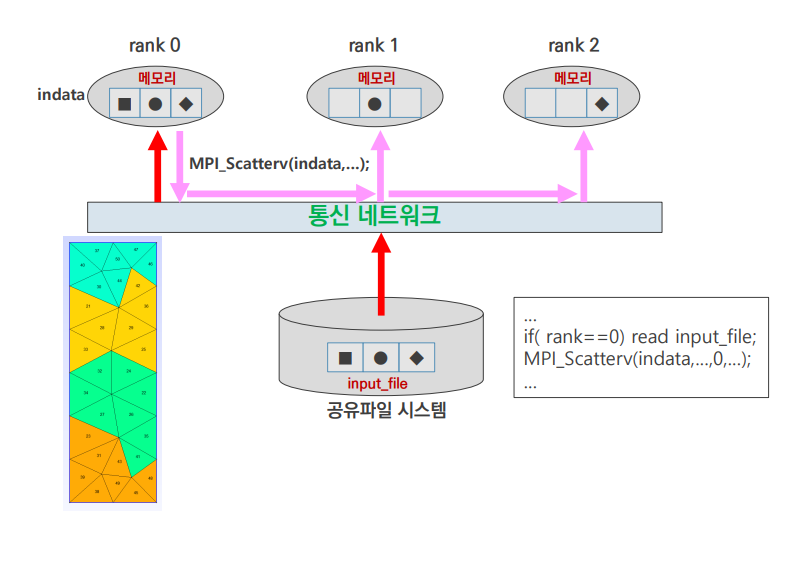
• 하나의 rank가 input data를 읽어들임
• 각 rank에 필요한 부분을 scatter
• broadcast에 비해 통신 효율이 좋아짐

input 4

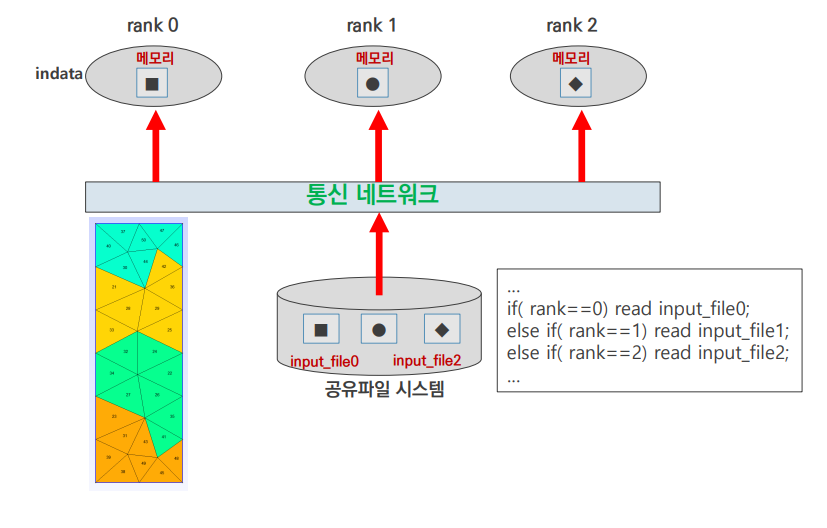
• 각 rank에서 필요한 data를 각자 읽어들이는 방식
• mesh file을 도메인 분할하여 따로 저장 후 input
• input file 관리가 복잡해질 수 있음

input 5

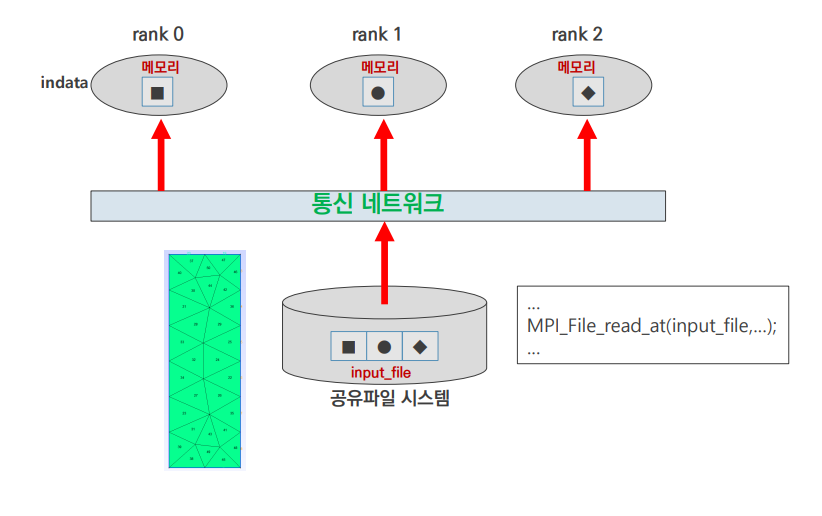
• MPI_File_read() 함수로 각 rank에서 필요한 부분을 read

2. Output

output 1

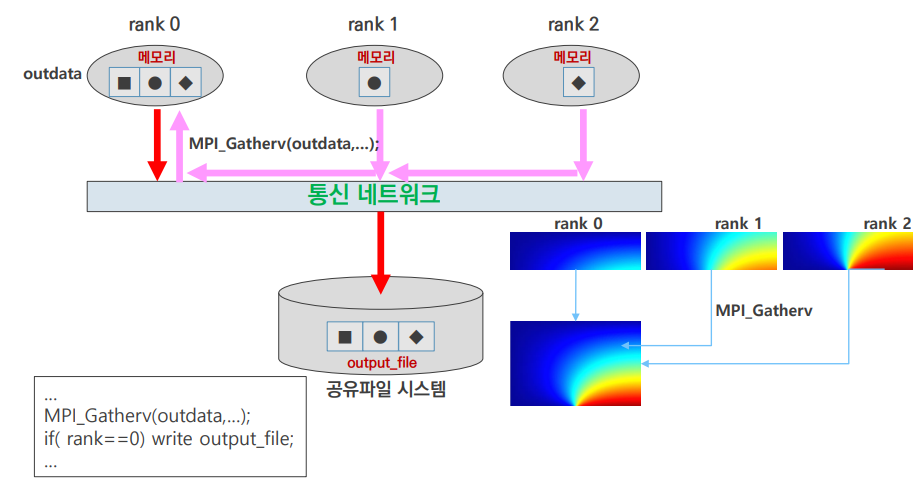
• MPI_Gatherv()로 한 rank에 취합 후 해당 rank에서 file write

output 2

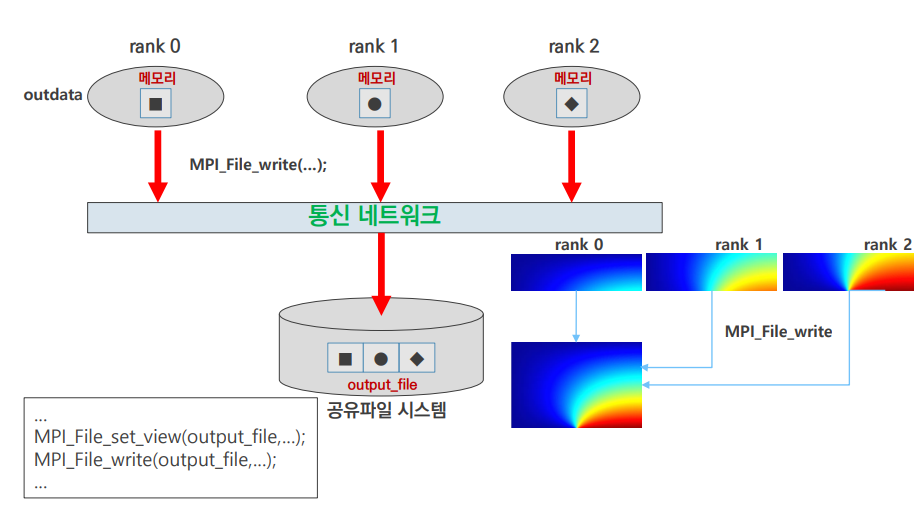
• MPI I/O 함수 사용
• 각각의 rank에서 자신이 연산한 부분을 output_file에 write

output 3

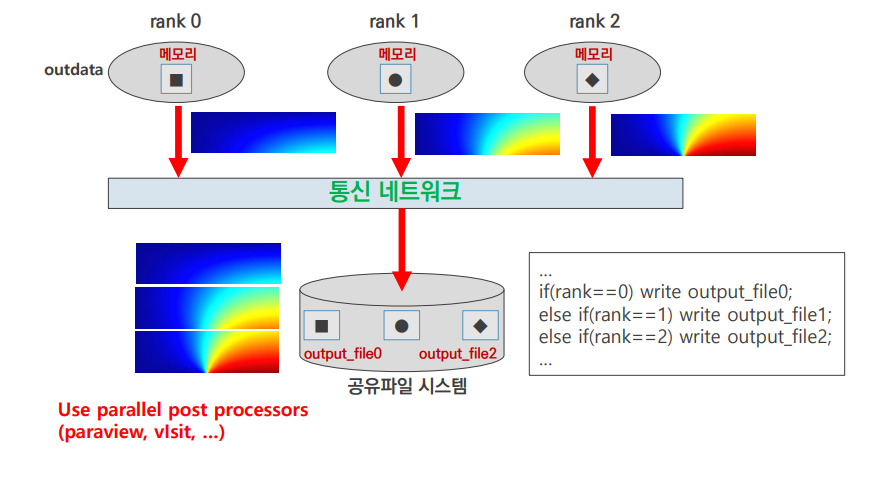
• 각각의 rank가 각자 다른 output file을 write
• prarview, visit 등 parallel post processors로 취합 & 분석
• 병렬 후처리 프로그램의 필요성

Loop 병렬화

1. Block Distribution

배수 관계 O

• MPI는 OpenMP나 CUDA와 다르게 자동 루프 병렬화 지원 X

배수 관계 X

n = p × q + r
n= r ( q + 1 ) + ( p - r ) q

• 반복 횟수 n, 프로세스 개수 p / 몫 q, 나머지 r
• r개의 프로세스에서 (q+1)번의 반복 + (p-r)개의 프로세서에서 q번의 반복을 수행하는 식으로 루프를 분할

block distribution function

void para_range(int n1,int n2, int nprocs, int myrank,int *ista, int *iend){
	int iwork1, iwork2,min_val;
	iwork1 = (n2-n1+1)/nprocs;
	iwork2 = (n2-n1+1) % nprocs;
	min_val= myrank>iwork2 ? iwork2 : myrank;
	*ista= myrank*iwork1 + n1 + min_val;
	*iend = *ista + iwork1 - 1;
	if(iwork2 > myrank) *iend = *iend + 1;
}

• 각 rank에서의 iteration start 위치와 iteration end 위치를 return

2. Cyclic Distribution

Cyclic Distribution

for(i = n1+myrank; i<=n2;i+= nprocs){
	// computation...
}

• stride = nprocs
• 반복문을 nprocs만큼 건너뛰며 실행 -> isend, iend 지정 필요 X
• load balancing에 유리 (ex. 반복마다 계산량이 늘어나는 연산)
• cache miss 다수 발생
  • cache에 데이터를 올릴 때, 이웃한 데이터를 동시에 가져감 -> 보통 이웃한 데이터를 같이 쓰는 block distribution에서는 문제 X but cyclic에서는 쓸모없는 데이터를 올려 캐시 낭비 가능성 up

Block-Cyclic Distribution

for(ii = n1+myrank*iblock; ii<=n2;ii+= nprocs*iblock){
	for(i = ii; i<=MIN(ii+iblick-1,n2);i++){
		computation
	} 
}

• block distribution의 load balancing 문제와 cyclic balancing의 cache miss문제를 해결하기 위한 절충안
• cyclic하게 돌아가며 block 단위로 루프 작업 수행

3. Nested Loop

Fortran

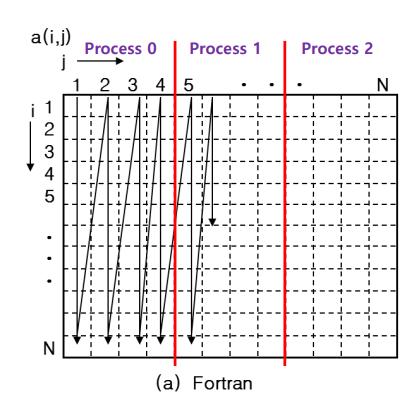
• 2차원 배열이 column 기준으로 linear하게 저장
• 프로세스 분할 시, column 기준으로 분할

C

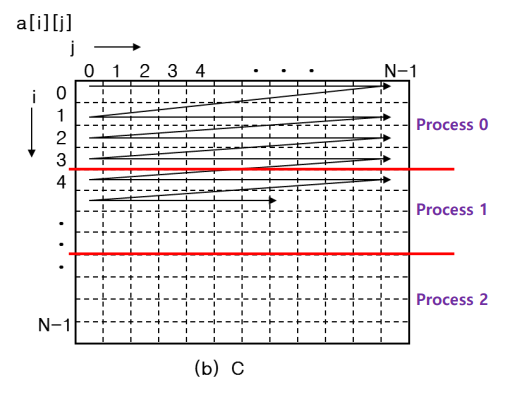
• 2차원 배열이 row 기준으로 linear하게 저장
• 프로세스 분할 시, row 기준으로 분할

Stencil 병렬화

1. 1D FDM

개요

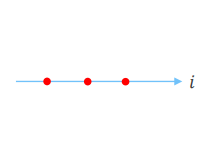
• 3-point stencil
• 가운데 점 계산을 위해 필요한 이웃 데이터 2개

Data Dependence and Movements

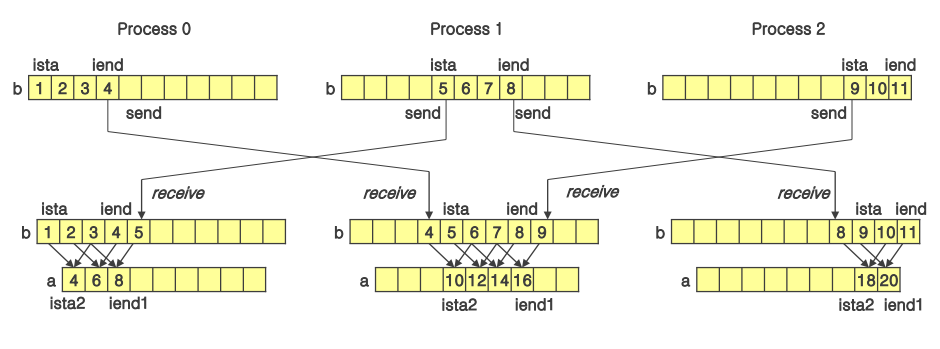
• a[i] = b[i] + b[i+2]
• 배열 b가 3개의 프로세스에 나누어 저장되어 있음
• MPI_Send(), MPI_Recv()로 통신하며 a 배열 완성

2. 2D FDM

개요

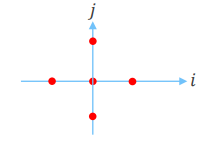
• 5-point stencil
• 가운데 점을 계산하기 위해 필요한 이웃 데이터 4개

Row-Wise

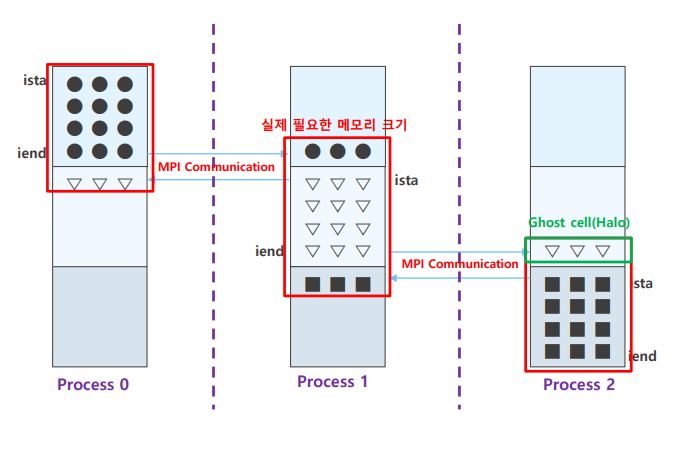
• C는 row-based 방식
• MPI 통신 함수로 바로 data를 전송하면 됨

Column-Wise

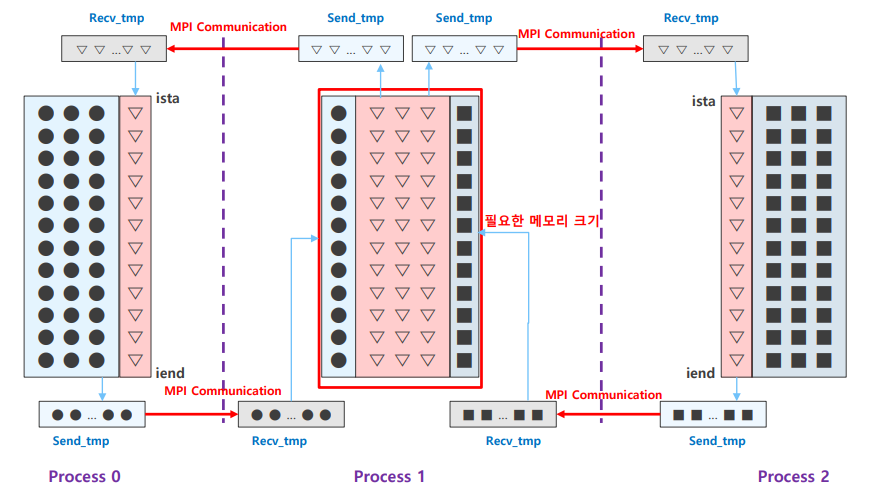
• column-wise는 통신 전 사전 작업이 필요
• 보내고 싶은 column의 data를 임시 버퍼 tmp에 저장하며 통신

Block distribution in both dimensions

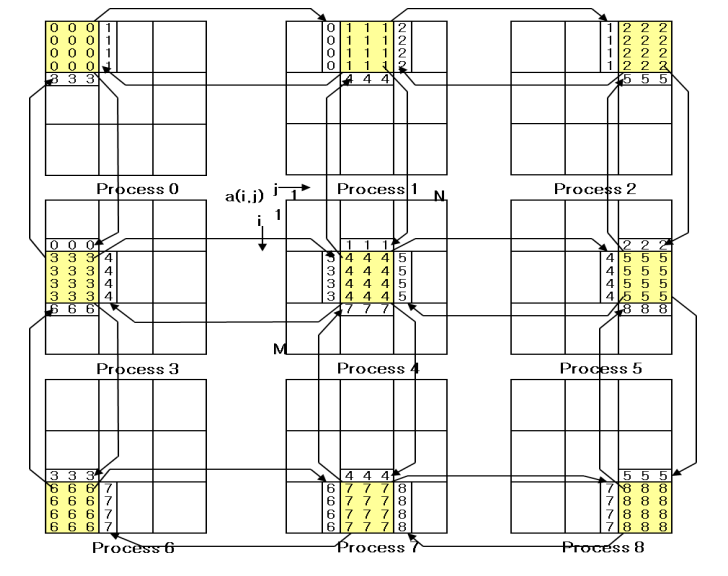
• 실제 FDM은 보통 양방향 통신
• row 전송은 쉽게 column 전송은 어렵게 수행함