Write Optimized Indices
쓰기 중심의 업무에 B+tree는 적합하지 않을 수 있음
- One I/O per leaf, 모든 internal node는 memory상에 있다고 가정
- with magnetic disk, 초당 100번 미만의 insert
- with flash memory, one page overwrite per insert
write의 cost를 줄이기 위한 두 가지 접근
- Log-structured merge tree
Log Structured Merge (LSM) Tree
쓰기 중심의 일을 위해 디자인됨
- 빠른 Insertion
- search 성능은 그저 그럼
key-value를 저장하는데 다양하게 사용됨
- Big table, Hbase, Cassandra, RocksDB등등
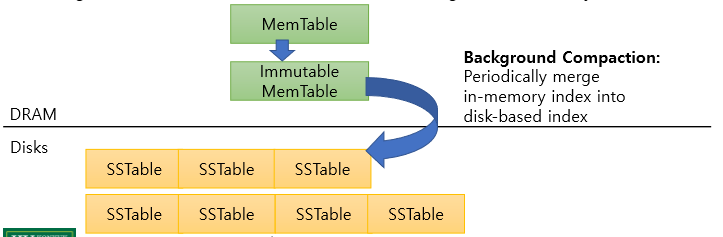
메모리상의 MemTable에 insert -> MemTable이 가득 차면 immutable MemTable로 전환 -> background에서 SSTable(sorted array) 형태로 Disk에 write
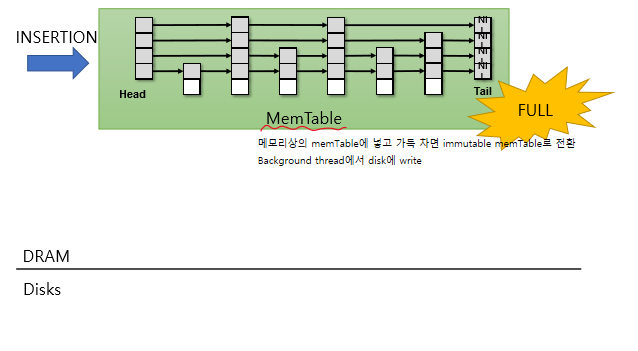
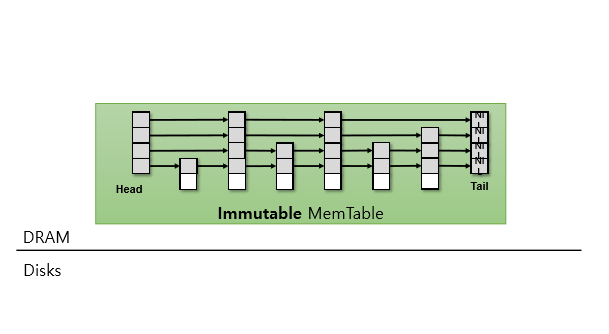
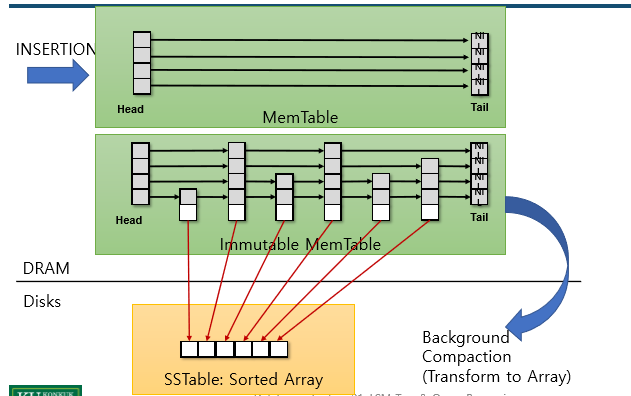
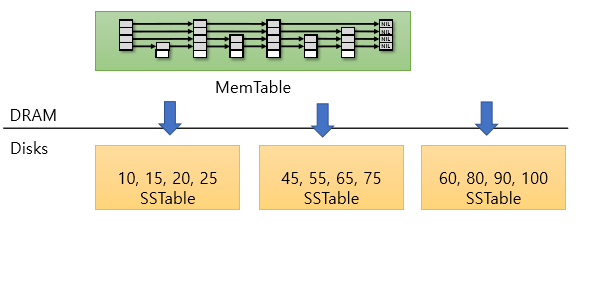
level 0의 뒤의 두 SSTable은 entry의 범위가 겹침 -> merge sort한 뒤 다음 level로 보냄
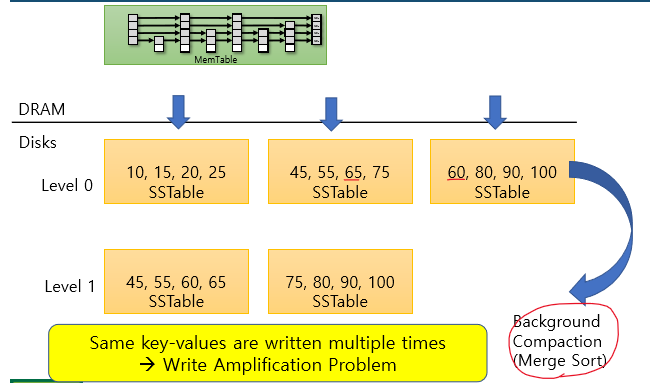
이런 식으로 쭉 반복해서 Disk에 저장
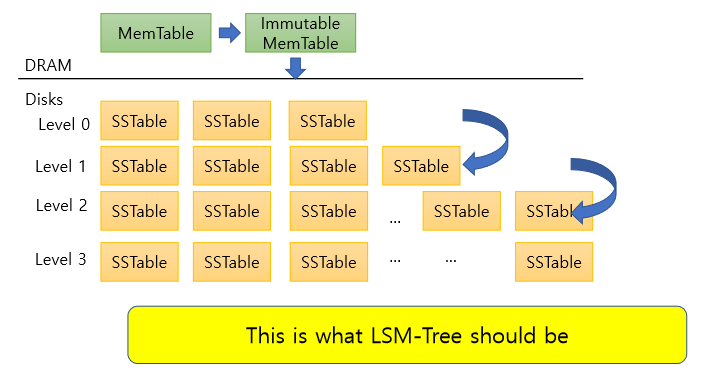
disk상의 SSTable을 merge sort하는 작업은 느리기 때문에 Immutable Table을 level0로 넘기지 못해 가득 찬 MemTable을 처리 못 하고 멈춰있을 수 있음 -> Write Stall problem
SkipList
random 기반의 data structure
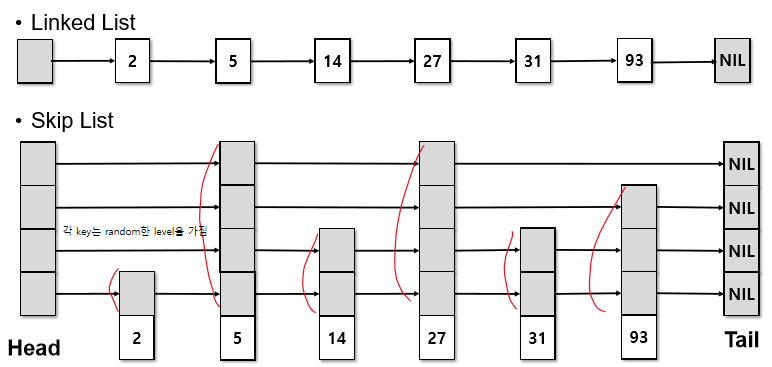
각 key가 random한 level을 가지는 linked list
search
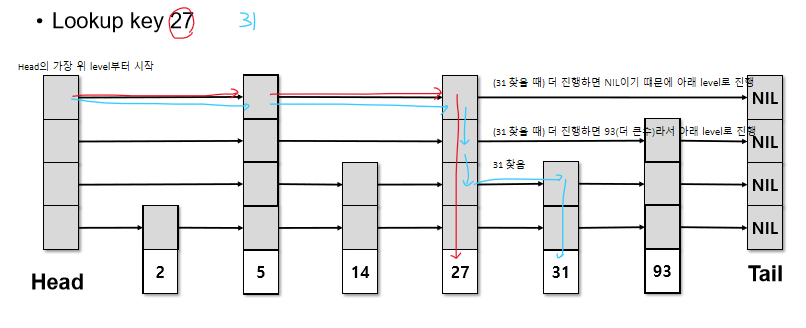
head 가장 위 level에서 시작
다음 pointer가 NIL이거나 찾는 key보다 크면 아래 level로 내려감
Insert
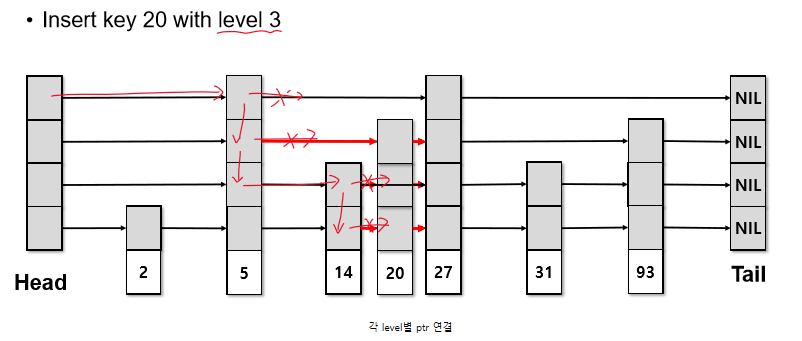
search와 동일하게 삽입 될 위치를 찾음, 삽입하고 random level 에 따라 pointer 연결
Delete
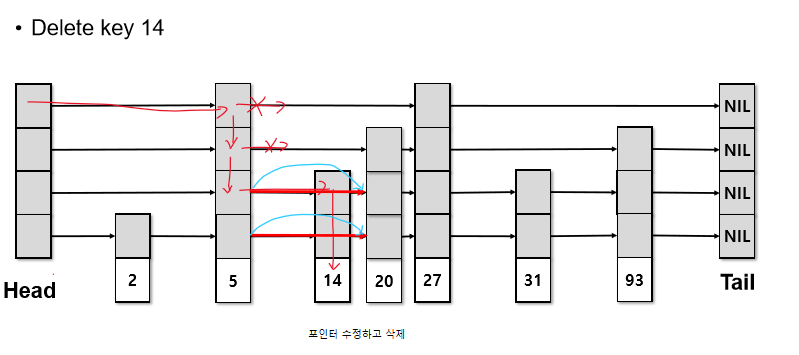
search와 동일하게 삭제할 key 찾아 삭제, pointer 처리
Basic Step in Query Processing
- Parsing and translation
- Optimization
- Evaluation
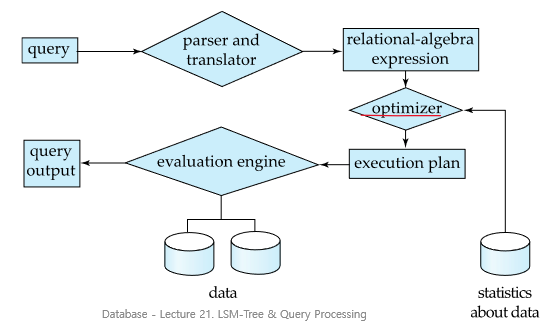
Parsing and translation
- parser가 syntax check, relation 확인
- query를 relational algebra로 translate
Evaluation
- query-execution engine은 query-evaluation plan을 가지고 실행함 그리고 query의 결과를 return함
Optimization
relational algebra expression은 같은 결과를 내는 다른 expression들이 있을 수 있음
각 relational algebra operation은 여러 algorithm으로 평가될 수 있음
query를 평가하기 위한 primitive operation의 sequence를 query-evaluation-plan이라고 함
Query Optimization: 같은 결과를 내는 모든 evaluation plan중 가장 비용이 낮은 것을 선택
- cost는 DB의 통계 정보를 통해 예측됨 (예) 각 relation이 가지는 tuple의 수, tuple의 크기 등)
Measures of Query Cost
Cost는 보통 total elapsed time으로 계산
Disk access는 cost의 많은 부분을 차지함, 예측하기도 쉬움
Disk access는 다음 항목들로 측정됨
- number of seeks * average-seek-cost
- number of blocks read * average-block-read-cost
- number of blocks written * average-block-write-cost
write cost가 read cost보다 큼
cost 측정을 단순화하기 위해 disk에서의 block transfer의 수와 seek의 수만 사용
- -time to transfer one block
- -time for one seek
- cost for b block transfers plus S seeks =
CPU cost는 무시
Selection Operation
File scan - The lowest level operator to access data
Algorithm A1(linear search) - 각 file block을 scan해 모든 record가 selection 조건을 만족하는지 확인
- Cost = block transfers + 1 initial seek
- : relaion r의 record를 포함하는 block의 수
- file block은 연속적으로 저장되어있다고 가정
unique key라면 보통 block을 절반정도 찾았을 때 찾았다고 가정
=> block transfer + 1 initial seek
Selection Using Index
Index scan - index를 사용하는 search algorithm
A2(primary B+tree index, equality on key)
- 조건을 만족하는 record 1개 검색
- Cost = 각 level에서 seek, transfer하므로
- = B+tree height
A3(primary B+tree index, equality on non unique key)
- 여러 record를 검색
- record는 연속되는 block에 있음
- b = 매칭되는 record를 가지는 block의 수
- Cost =
A4(secondary index, equality on non unique key)
- retrive multiple records if search key is not a candidate key
- 각 n개의 매칭되는 record는 다른 block에 있을 수 있음
- Cost =
Selection Involving Comparisons
selection에 비교연산자가 조건으로 들어가는 경우
A5(primary B+tree index, comparison)
- Cost =
A6(secondary B+tree index, comparison)
- Cost =
Sorting
memory에 맞는 relation -> quick sort
memory에 맞지 않는 relation -> external sort-merge
External Sort-Merge
memory size에 맞게 load할 페이지의 개수 M 설정
- 정렬된 run 생성. 초기 i = 0
relation이 끝날 때까지 반복
a. relation의 M block을 memory로 read해온다
b. memory상에서 sort함
c. sort된 data를 run 로 write, i++
반복이 끝났을 때의 i를 N이라 하자 - Merge the runs (N-way merge)
N < M이라고 가정
1. 메모리에서 N block을 buffer로 사용, 1 block을 output buffer로 사용. 각 run의 첫 block을 buffer로 read함
2. 아래 내용을 반복
a. buffer에 있는 record들 중 가장 작은 record를 선택
b. 해당 record를 output buffer에 write output buffer가 full이면 disk에 flush
c. buffer에서 해당 record 삭제, 삭제된 record가 있던 run의 다음 block read해 buffer에 삽입 - 모든 buffer가 empty가 될 때까지 반복
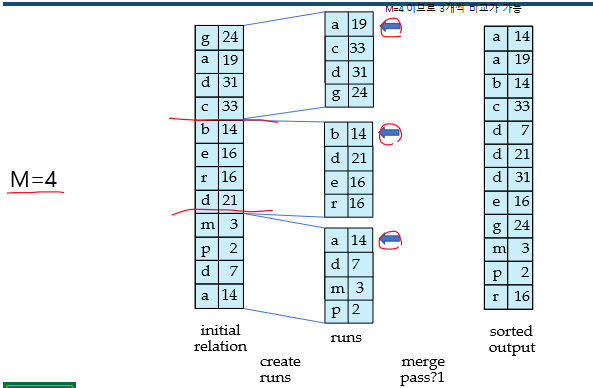
만약 인 경우 몇몇 merge는 pass가 필요
- 각 pass에서 최대 연속되는 M-1개의 run들이 merge됨
- pass는 M-1을 factor로 run의 개수를 줄임
- run이 하나가 될 때까지 반복
- 간단하게 말하면 step을 나눠 merge하겠다는 의미
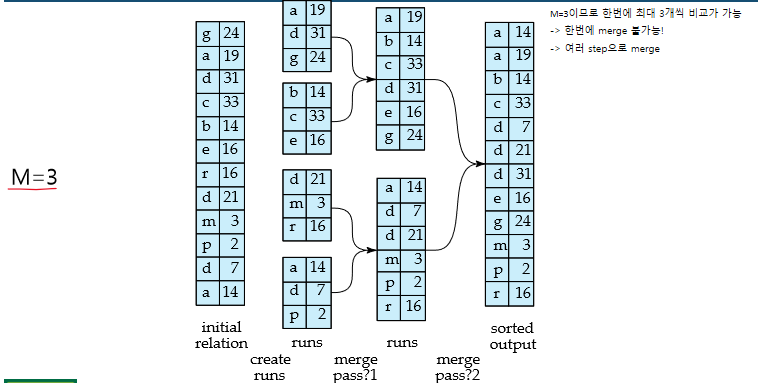
Cost analysis