Normalization

Schema 합치기

여러 table을 합치면 장단점이 있다.
장점: 정보를 찾기 편해짐
단점: 테이블이 커짐, 반복되는 값이 생김

Smaller schema

그렇다면, schema를 최대한 작게 쪼개는게 좋은 것일까?
각 attribute의 funcional dependency를 확인해보면 됨
어떤 attribute에 따라 결정되는 attribute들 <- functional dependency가 있다. (candidate key와 나머지 attribute의 관계)

candidate key가 아닌 걸 기준으로 쪼개면? lossy decomposition이 됨 말 그대로 데이터 손실이 생김

예시)

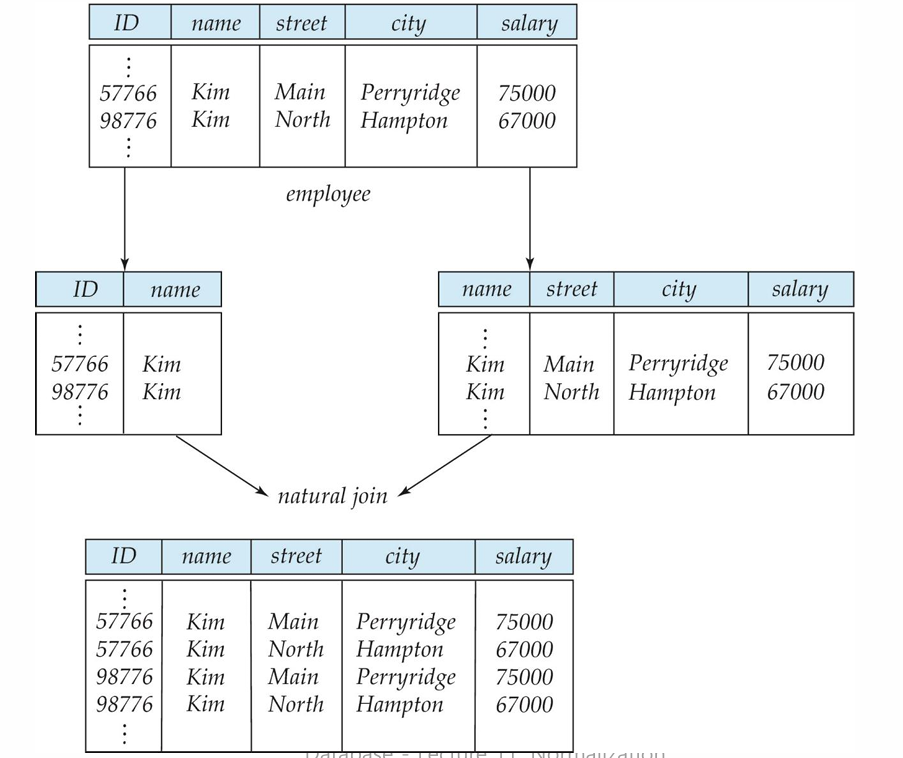
employee를 분해하고 다시 합치는 과정에서 원본 table과 데이터가 달라졌음을 확인 할 수 있다.

First normal form

모든 attribute의 value는 atomic해야 함.
즉, 한 attribute에다가 여러 value 넣지 마라, composite attribute 넣지 마라

예시) member 테이블에 phone_num attribute가 있다고 하면, 한 사람이 여러 전화번호를 가질 수 있다. 그렇다고 phone_num 에다가 (010-xxxx-xxxx, 010-yyyy-yyyy) 이렇게 넣지 말라는거다.

Functional Dependency

relation R이 있을 때,
$\alpha\sube R\enspace and\enspace\beta\sube R$

functional dependency
$\alpha\to\beta$
이면, 두 tuple $t_1$, $t_2$의 attribute $\alpha$가 같으면, $\beta$도 같아야 함
$t_1[\alpha]=t_2[\alpha]\implies t_1[\beta]=t_2[\beta]$

예시)

A	B
1	4
1	5
3	7

$A\not\to B$이다. 하지만 $B\to A$는 성립한다.

relation R의 key K가 $K\to R$이면 K는 super key 이다.

$K\to R$ 이고, 어떤$\alpha\sub K$에 대해 $(K-\alpha)\to R$이 되는 $\alpha$가 없으면 K는 candidate key이다 (최소 attribute super key라는 뜻)

Trivial
$\alpha\to\beta$일 때, $\beta\sube\alpha$이면 Trivial한 functional dependency라고 한다.

Closure
우리는 functional dependency 여러개로 또 다른 functional dependency를 추론해 낼 수 있다.
예시)$A\to B,\enspace B\to C$가 있으면, $A\to C$를 추론할 수 있음

functional dependency의 집합 F가 있을때, F로 추론할 수 있는 모든 functional dependency들의 집합을 F의 closure라고 하고, $F^+$로 표시한다.
$F^+$는 F의 superset(원래 FD+추론된 FD)

Properties of FD

Subset property(Trivial)
$IF\enspace Y\sube X,\enspace then\enspace X\to Y$
Augmentation
$IF\enspace X\to Y,\enspace then\enspace XZ\to YZ$
Transitivity
$IF\enspace X\to Y\enspace and\enspace Y\to Z,\enspace then\enspace X\to Z$
Union
$IF\enspace X\to Y\enspace and\enspace X\to Z,\enspace then\enspace X\to YZ$
Decomposition
$IF\enspace X\to YZ,\enspace then\enspace X\to Y\enspace and\enspace X\to Z$
Pseudo-transitivity
$IF\enspace X\to Y\enspace and\enspace WY\to Z,\enspace then\enspace WX\to Z$

Boyce-Codd Normal Form

relation R의 $F^+$의 모든 FD $\alpha\to\beta$가 다음 조건 중 최소 하나를 만족해야 함

• $\alpha\to\beta$ is trivial (즉, $\beta\sube\alpha)$
• $\alpha$ is super key for R

Decomposing a Schema into BCNF

우선 BCNF를 깨는 FD를 찾는다 $\alpha\to\beta$라고 하면,
R을 다음 두 relationd로 분해
$(\alpha\cup\beta)\enspace and \enspace (R-(\beta-\alpha))$

예시)
instr_dept(ID, name, salary, dept_name, building, budget)
$dept\_name\to building,\enspace budget$
dept_name은 instr_dept의 super key도 아니고, 위 FD는 Trivial도 아니다. 따라서 BCNF를 깨는 FD이다.
$\alpha=dept\_name$
$\beta=building,budget$ 에 해당

$(\alpha\cup\beta)=$(dept_name, building, budget)
$(R-(\beta-\alpha))=$(ID, name, salary, dept_name)
하면 BCNF된 relation이 됨

dependency를 보존하면서 BCNF로 decomposition하는 것이 불가능 할 수도 있음
그래서 보통은 Third normal form으로 분해함

Third Normal Form

다음을 충족하면 relation R은 3NF이다.
모든 $\alpha\to\beta\enspace in\enspace F^+$에 대해 다음 중 적어도 하나를 만족해야 함

• $\alpha\to\beta$ is trivial
• $\alpha$는 R의 super key
• $\beta-\alpha$의 각 attribute A는 R의 candidate key에 포함되어야 함

R이 BCNF면, 3NF임(모든 FD가 조건1 or 2를 충족하므로)
3번째 조건이 dependency preservation을 위한 조건

3NF의 장점

• dependency preservation 보장

3NF의 단점

• null value를 사용해야 할 수도 있음
• 중복되는 value가 있을 수 있음

Normalization의 목표

Benefits of normalization

• Less strage space
• Quicker update
• Less data inconsistency
• Clearer data relationships
• Easier to add data
• Flexible structure