A/B Tests for Engineers (번역)

ref.
https://win-vector.com/2023/10/15/a-b-tests-for-engineers/

Introduction

A/B 테스트의 엔지니어링 스타일:

시스템이 주장한 대로 작동하는지 확인하기 위해 시뮬레이션된 예제를 작동합니다.

문제를 해결하려고 시도하기 전에 문제의 예를 보여줄 것입니다.

우리는 모든 상위 수준의 주장을 계산으로 보여줄 것이며, 이를 참조에 위임하지 않을 것입니다.

우리는 기본적인 수학은 참고 문헌에 맡기고 다시 도출하려고 하지 않을 것입니다.

Set Up

일반적인 A/B 테스트의 관심사는 비율의 차이를 측정하는 것입니다. 각각의 실험 데이터에 대해 “확률 P[A]”로 원하는 것을 수행하는 시스템과 “확률 P[B]”로 원하는 것을 수행하는 시스템이 있습니다. (P[A], P[B]는 알 수 없음. 추정 예정) 우리는 임계값 t >= 0일 때, P[B] - P[A]>= t 인지 판단하는 것입니다. 즉, "B"의 전환율이 "A"의 전환율보다 크게 개선되었는지를 알고 싶습니다.

이를 예제와 시뮬레이션으로 확장해 보겠습니다. 두 개의 장바구니 결제 인터페이스와 반복되지 않는 방문자가 있다고 가정해 보겠습니다. 온라인 쇼핑 결제 프로세스 후반부에 사용자 인터페이스의 변형을 테스트하고 있습니다. 품목 보고 방식, 결제 지정 방식 등을 테스트하고 있을 수 있습니다. 사용자와의 상호 작용 방식에 따른 장바구니 완료율에 관심이 있습니다.

우리 모두 "A"(또는 "대조군(Control)" 또는 "챔피언"이라고 부르는)라고 부르는 현재 시스템이 있고 "B"(또는 "실험(Treatment)" 또는 "도전자"라고 부르는 새로운 프로세스가 있습니다.) "B"가 "A"에 비해 크게 개선되었는지 아닌지를 높은 신뢰도로 확인하려면 얼마나 많은 샘플이 필요할까요?

우리의 실험은 2 * n 개의 결제 샘플을 수집하고 그 중 n 개를 무작위로 A, B에 할당하는 것입니다. 선택한 임계값 t >= 0 에 대해 관찰된 “평균(B) - 평균(A) >= t”인 경우, "B"가 "A"보다 더 잘 나타난다고 말합니다.

사용자는 A/B 테스트를 결정하는 세 가지 매개 변수를 지정합니다:

r: “Large Improvement"에 대한 정의입니다. 성공 확률이 얼마나 크게 변화했는지를 나타냅니다. mean(B) - mean(A) >= t. 일반적으로 신뢰할 수 있는 테스트는 0 < t < r입니다.

유의도(Significance): 원하는 위양성률(False Positive) 또는 유의도(Significance)입니다. 이는 실제로는 개선되지 않았음에도 "큰 개선"이라는 잘못된 인식을 받아들일 수 있는 빈도입니다.

검정력(Power): 원하는 진양성률(True Positive) 또는 민감도(Sensitivity). 이는 큰 개선을 올바르게 인식하고자 하는 빈도입니다.

위의 Parameter가 주어지면 선택할 수 있습니다:

t: observe_mean(B) - observe_mean(A) >= t 를 강한 양성 증거(Positive Evidence)로 간주하는 임계값입니다.

n: "A"와 "B"에서 테스트할 항목의 수입니다.

n과 t를 올바르게 선택하고 테스트를 올바르게 실행하면 유의도(Significance)와 검정력(Power) 요건을 충족하는 신뢰할 수 있는 테스트가 됩니다.

우리는 두 환경 중 하나에 있다고 가정합니다. 한 환경는 귀무가설 H0 또는 A/A 환경으로, B 프로세스가 정확히 A 프로세스입니다. 다른 하나는 P[B 완료] - P[A 완료] >= r인 크게 개선된 환경 H1입니다. 두 환경 모두에서 올바른 테스트 절차를 설계한 다음 이를 사용하여 우리가 어느 환경에 속할 가능성이 높은지 결정할 수 있습니다.

유의도(Significance) 값은 0에 가깝게 조정해야 여러번 테스트하고 다중 비교 문제(Multiple Comparison Problem)를 방지할 수 있습니다. 다중 비교 문제(Multiple Comparison Problem)는 본질적으로 "예"가 나올 때까지 반복해서 테스트하는 프로세스의 불안정성입니다.

검정력(Power) 값은 20%의 크게 개선된 환경인 "B"를 버리지 않을려면 1에 가깝게 이동해야 합니다.

A 또는 B가 모두 새로운 대안이고 어느 쪽이 더 나을 수 있는 양방향 검증을 사용하는 경우, 비모수검정의 사후분석(Bonferroni Correction)을 통해 유의도(Significance)를 절반으로 줄여야 합니다.

An example

다음과 같이 지정하여 가정해 보겠습니다:

r = 0.1(전환율을 10% 개선하는 데에 관심이 있음을 의미).

유의도(Significance) = 0.02(오양성률(False Positive Rate) 2%를 허용한다는 의미)

검정력(Power) = 0.9(90%의 진양성률(True Positive Rate) 또는 민감도(Sensitivity)를 원한다는 의미).

관찰된 결과와 실제로 행동이 다른지 알고 싶습니다. A와 B 코드가 있고 다음과 같이 설정하였습니다.

# prepare our pseudo-random number generator
rng = np.random.default_rng(2023)

# specify our user parameters
r = 0.1
significance = 0.02
power = 0.9
assert (r > 0) and (r < 1)
assert (significance > 0) and (significance < 0.5)
assert (power > 0.5) and (power < 1)

# define our stand in experiments
def a_completed() -> float:
    "Simulate an event that is 1 47% of the time, and 0 otherwise"
    return float(rng.binomial(n=1, p=0.47, size=1)[0])

# define the B process
def b_completed() -> float:
    "Simulate an event that is 1 57% of the time, and 0 otherwise"
    return float(rng.binomial(n=1, p=0.57, size=1)[0])

"A"함수와 "B"함수를 각각 n번씩 호출하고 관찰된 평균 차이를 계산하여 실험을 시뮬레이션할 수 있습니다.실제로는 데이터를 수집하여 실제 A/B 테스트를 실행합니다. 모든 데이터를 단일 테스트에 결합하는 것이 여러번 테스트하는 만큼 강력하기 때문에 동일한 설정에서 여러 개의 A/B 테스트를 계획하는 경향이 있습니다. 그러나 좋은 결과가 예상되는 경우 추가(그리고 더 큰 규모의) 테스트를 통해 후속 조치를 취하는 것이 좋습니다. 즉, A/B 테스트 실행은 다음과 같습니다. 다음은 A와 B 각각에 대해 20개의 샘플를 시도하는 예시입니다.

# simulate estimating the difference in means
def estimate_empirical_mean_difference(*, a_source, b_source) -> float:
    """
    Estimate mean(b_source) - mean(a_source) using n samples of each.
    :param a_source: list of a-measurements.
    :param b_source: list of b-measurements.
    :return: mean(b) - mean(a)
    """
    return np.mean(b_source) - np.mean(a_source)

# trying to detect if this is A or B from the returned result
estimate_empirical_mean_difference(
    a_source=[a_completed() for i in range(20)],
    b_source=[b_completed() for i in range(20)])

Out:
-0.09999999999999998

질문은 다음과 같습니다:

20개가 적절한 샘플 수인가?

관찰된 결과가 실용적인 관점에서 의미있는 값인가? 이를 임상적 유의성(Clinical Significance)이라고 하며, 도메인 특수성(Domain Specific) 문제입니다. 예를 들어, 전환율의 변화 값 자체가 정당화할 만큼 충분한 수익을 창출하고 있는가?

관찰된 결과가 신뢰할 수 있는 측정치라고 주장할 수 있을 만큼 충분히 큰가? 이를 통계적 유의성(Statistical Significance)이라고 하며 신뢰성(Reliability)에 관한 문제입니다.

실험은 두 가지 방식으로 우리를 속일 수 있습니다:

실제로는 차이가 없는데도 A와 B 사이에 큰 차이가 있다고 주장할 수 있습니다. 이를 위양성(False Positive) 또는 유의성 실패(Significance Failure)라고 합니다.

실제로는 차이가 있는데도 A와 B 사이에 큰 차이가 없다고 주장할 수 있습니다. 이를 위음성(False Negative) 또는 검정 실패(Power Failure)라고 합니다.

이러한 실패의 몇 가지 예를 살펴보겠습니다.

The “no difference” case or A/A case

시도해 볼 만한 흥미로운 경우는 "B"가 "A"보다 나을 것이 없는 경우입니다. 이를 통해 실험의 유의성 또는 오탐률을 제어할 수 있습니다.

시뮬레이션 데이터를 사용하면 알려진 상황에서 이러한 실험을 여러 번 실행할 수 있습니다. 이를 통해 주장된 테스트 또는 측정 절차의 신뢰성을 평가할 수 있습니다.
작은 A/A 테스트("B"가 "A"와 동일한 것으로 알려진 경우라고 함)를 실행해 보겠습니다. 실제 이론적 평균 차이는 0이지만, 표본 크기가 작은 경우 실험은 종종 이 값과 다른 값을 반환합니다.

# run a few super small (and therefore unreliable) experiment
[estimate_empirical_mean_difference(
    a_source=[a_completed() for i in range(20)],
    b_source=[a_completed() for i in range(20)]) for i in range(10)]

Out:
[-0.2, 0.050000000000000044, 0.050000000000000044, -0.19999999999999996, 0.25,
 -0.2, -0.10000000000000003, -0.15000000000000002, -0.2, -0.19999999999999996]

테스트 10회 반복에 대해 매우 다른 값이 나온 것을 알 수 있습니다. 이는 사용된 n=20이 테스트 크기가 너무 작다는 증거입니다.
다시 말하지만, 실제로는 보통 초기 실험을 한 번만 실행합니다. 사전 실험 자원이 더 많으면 동일한 설정에서 더 많은 테스트를 실행하는 것이 아니라 더 큰 규모의 테스트를 실행합니다.

First stab at test size.

이제 개선되지 않은 "B"가 "A"보다 훨씬 더 나은 것으로 착각하지 않도록 필요한 실험의 크기를 계산해 보겠습니다. 주어진 테스트 임계값에 대해 필요한 실험 크기(또는 A와 B에 각각 전송할 항목 수)를 반환하는 함수가 있다고 가정해 보겠습니다. 이 함수를 사용하면 다음과 같이 실험을 설계할 수 있습니다. 이 함수를 사용하되 일부러 t = r 로 설정하는 실수를 해 보겠습니다.
전환율 10% 향상을 목표로 한다면 10%를 임계값으로 사용하는 것이 합리적으로 보일 수 있습니다. 이것이 왜 우리가 실제로 원하는 것이 아닌지 살펴보겠습니다. 이 실험 설계 오류는 A/A 사례에서 문제를 일으키지 않습니다. 차이가 있을 때 이를 감지하려고 할 때만 비로소 문제를 발견할 수 있습니다.

# make our error
t = r

# get the sample size for significance goal (while neglecting power)
n_sig_wrong = int(np.ceil(
    find_n_for_given_mass_of_binomial_left_of_threshold(
        mass=1-significance, threshold=t)))
n_sig_wrong

Out:
211

이제 A/A 실험을 여러 번 실행하여 관찰된 평균 차이가 이 임계값을 얼마나 자주 초과하거나 하회하는지 확인해 보겠습니다.

# how many times we will repeat our run
n_repeat_trials = 10000

false_positive_rate_1 = np.mean([
    estimate_empirical_mean_difference(
        a_source=[a_completed() for i in range(n_sig_wrong)],
        b_source=[a_completed() for i in range(n_sig_wrong)]) >= t \
    for i in range(n_repeat_trials)])

assert np.abs(false_positive_rate_1 - significance) < 1e-2
false_positive_rate_1

Out:
0.018

유의성(Significance) 측면에서 보면 대단한 결과입니다. 이 실험은 설계된 대로 임계값을 2% 정도만 초과했습니다. 개선되지 않은 항목을 거부하는 작업에서 원하는 오류율은 2%입니다. 이제 B != A 사례에서 t=r 설정이 잘못된 이유를 살펴보겠습니다.

Power failure

이 실험이 얼마나 자주 결정 임계값(Decision Threshold)을 초과하는지, 차이를 감지할 수 있는지 살펴봅시다. 결과가 개선 사항을 정확하게 알아차릴 수 있는 경우이므로 이 값이 커지기를 원합니다.

true_positive_rate_1 = np.mean([
    estimate_empirical_mean_difference(
        a_source=[a_completed() for i in range(n_sig_wrong)],
        b_source=[b_completed() for i in range(n_sig_wrong)],
    ) >= t for i in range(n_repeat_trials)])

np.abs(true_positive_rate_1 - power) < 1e-2
# observed true_positive_rate_1 (0.4827), not where we hoped (0.9)
true_positive_rate_1

Out:
0.4827

관찰된 실제 진양성률(True Positive Rate) 또는 민감도(Sensitivity)가 0.5에 가깝게 나왔고, 우리가 원하는 검정력(Power) = 0.9 가 아닌 것을 알 수 있습니다. 이는 개선된 B 프로세스의 절반을 버리게 된다는 의미입니다. 이를 그래프로 살펴봅시다.

display(binomial_diff_sig_pow_visual(
    stdev=np.sqrt(0.5 / n_sig_wrong), effect_size=r, threshold=r,
    title=f"(power failure) size={n_sig_wrong}, decision threshold = {r:.2f}",
    subtitle="1-power or false-negative-rate is 0.5 (large, bad)"))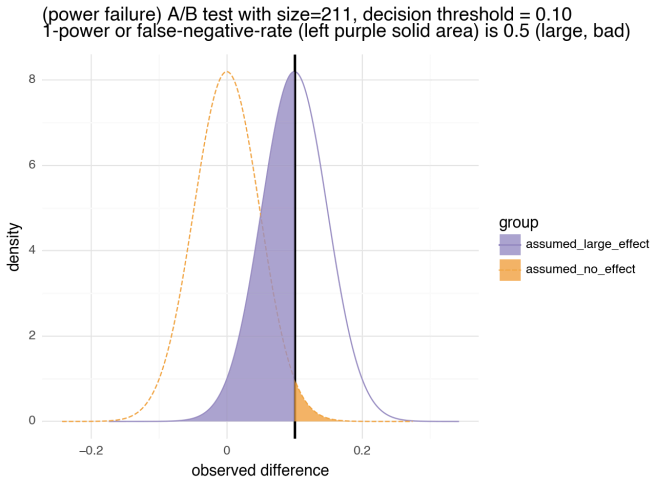

이 그래프에서 음영 처리된 영역은 모두 실험 오류 또는 실패 확률을 나타냅니다. 왼쪽 영역은 1 - 검정력(Power), 즉 위음성률(False Negative Rate)을 나타냅니다. 오른쪽 영역은 유의도(Significance) 또는 오양성률(False Positive Rate)을 나타냅니다. 좋은 실험 설계에서는 두 영역이 동시에 작습니다.

검정 실패(Power Failure)은 두 가지 관련 원인에 의해 발생합니다:

실험 설계의 어느 곳에서도 검정력(Power)을 사용하지 않았는데 왜 실험의 민감도(Sensitivity)가 검정력(Power)에 근접할 것으로 예상할 수 있을까요?

우리는 t=r 을 의도적으로 사용하고 있습니다. "A"와 "B"의 실제 차이는 정확히 r이며 분포는 거의 대칭입니다. 따라서 우리는 이 값보다 높거나 낮은 실험 결과를 거의 절반 정도 볼 수 있습니다.

t=r을 사용하는 이러한 유형의 대규모 실험은 거의 1/2에 가까운 관찰된 검정력(Power) 또는 진양성률(True Positive Rate)을 경험할 수 있습니다.
t=r 같은 "검정력(Power) 실수"가 드물기를 바랄 수도 있습니다. 안타깝게도 실제로는 흔한 것으로 보입니다. 코헨이 "행동 과학을 위한 통계적 검정력 분석"을 저술한 이유 중 하나이며, 이 책에서는 "기준"("결정 임계값"이라고 부르는 것)이 가정된 모집단 효과와는 다른 표본 효과라는 문제를 다루고 있습니다. 그러나 현재 많은 튜토리얼이 이러한 구분을 하지 못하고 있으며, 실험을 잘못 설계하여 암시적(심지어 숨겨진) t=r 검정 실패(Power Failure)로 유인할 수 있다는 사실을 발견했습니다.

Significance failure

이전에 유의도(Significance)를 중심으로만 실험을 설계했던 것과 달리 검정력(Power) 중심으로만 실험을 설계하면 비슷한 실패를 경험하게 됩니다. 이제 검정력(Power) 또는 민감도(Sensitivity)를 고려하여 설계해 보겠습니다. P(B) - P(A)>= t일 때 90%의 확률로 양수 표시를 얻을 수 있습니다(지금은 의도적으로 민감도(Sensitivity)를 무시하겠습니다).

t = 0 # another wrong threshold

# mass_to_right is 1-mass_to_left
n_power_wrong = int(np.ceil(find_n_for_given_mass_of_binomial_left_of_threshold(
                                mass=power, threshold=r - t)))
n_power_wrong

Out:
83

display(binomial_diff_sig_pow_visual(
    stdev=np.sqrt(0.5 / n_power_wrong), effect_size=r, threshold=0.0,
    title=f"(significance failure) size={n_power_wrong}, decision threshold = 0",
    subtitle="significance or false-positive-rate is 0.5 (bad)"))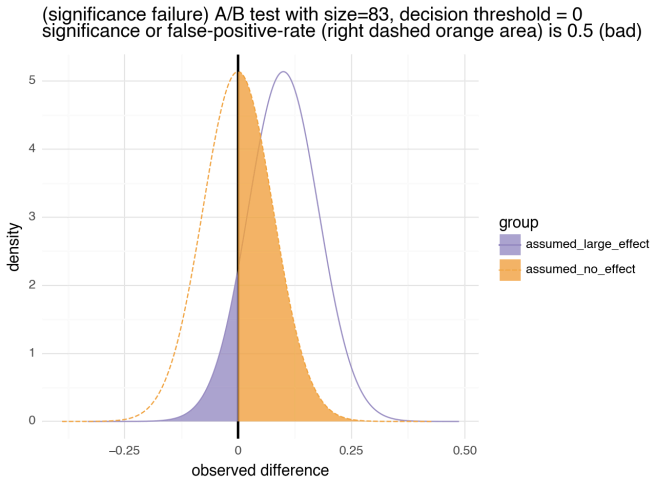

위의 테스트에는 결함이 있습니다. "A/A"의 경우를 절반은 "상당한 개선"으로 잘못 받아들인다는 것입니다.해당 사례는 결정 임계값을 사용하지 않고 관찰된 개선이 개선의 증거로 받아들여지는 일반적인 관행 하에서 정확히 일어나는 일입니다.

Designing a correct experiment

임계값을 가정한 영향(Effect Size) 또는 0으로 설정한 A/B 테스트는 실수라는 점을 분명히 이해하셨기를 바랍니다. 이제 올바른 테스트 임계값을 찾아봅시다.
테스트 임계값 t는 0과 r 사이에서 엄격하게 선택해야 합니다. 이렇게 하면 작은 오양성(False Positive) 확률 값과 큰 진양성(True Positive) 확률 값을 동시에 확보할 수 있습니다.

주어진 t에 대해 두 값 모두 필요합니다:

n >= find_n_for_given_mass_of_binomial_left_of_threshold(mass=1-significance, threshold=t) : 오양성률(False Positive Rate)이 낮을 만큼 충분히 큰 n

n >= find_n_for_given_mass_of_binomial_left_of_threshold(mass=power, threshold=r - t) : 진양성률(True Positive Rate)이 높을 만큼 충분히 큰 n

임의의 t에 대해 이 두 가지 기준을 모두 만족하는 n을 선택합니다. n은 실험을 실행해야 하는 시간이므로 n이 작도록 t를 선택하려고 합니다.

# get the threshold adjustment
threshold_adjust = find_threshold_adjustment(
    power=power, significance=significance,)

# 이는 t = 0.616 * r을 선택해야 하는 것이며, 지금은 그렇게 진행합니다.
t =  r * threshold_adjust
print(f"threshold_adjust: {threshold_adjust}, t: {t}")

# 이 임계값 t에 대해 두 기준을 모두 충족하는 새로운 n을 얻습니다.
n_sig = int(np.ceil(find_n_for_given_mass_of_binomial_left_of_threshold(
                        mass=1 - significance, threshold=t)))
n_power = int(np.ceil(find_n_for_given_mass_of_binomial_left_of_threshold(
                        mass=power, threshold=r - t)))
print(f"n_sig: {n_sig}, n_power: {n_power}")

assert n_sig == n_power

Out:
threshold_adjust: 0.615761286067465, t: 0.06157612860674651
n_sig: 557, n_power: 557

# 이 t에 대해 두 조건에서 실제로 동일한 n을 얻습니다.
n = int(np.max([n_sig, n_power]))
del n_sig, del n_power

이 새로운 n이 처음에 사용한 것보다 더 큰 것을 알 수 있습니다. 이는 새로운 임계값이 이전에 사용했던 임계값보다 훨씬 작기 때문입니다. 따라서 안정적으로 감지하려면 더 큰 n이 필요합니다.
이제 새로운 t와 n으로 실험을 실행합니다.

false_positive_rate_2 = np.mean([
    estimate_empirical_mean_difference(
        a_source=[a_completed() for i in range(n)],
        b_source=[a_completed() for i in range(n)]) >= t \
    for i in range(n_repeat_trials)])
true_positive_rate_2 = np.mean([
    estimate_empirical_mean_difference(
        a_source=[a_completed() for i in range(n)],
        b_source=[b_completed() for i in range(n)]) >= t \
    for i in range(n_repeat_trials)])

assert np.abs(false_positive_rate_2 - significance) < 1e-2
assert np.abs(true_positive_rate_2 - power) < 1e-2

false_positive_rate_2, true_positive_rate_2

Out:
0.0215, 0.8998

false_positive_rate_2: 약 2%의 지정된 유의도(Significance) 또는 오양성률(False Positive Rate)가 있음을 알 수 있습니다.

true_positive_rate_2: 검정력(Power). 민감도(Sensitivity) 또는 진양성률(True Positive Rate)이 90%로 표시됩니다.

display(binomial_diff_sig_pow_visual(
  stdev=np.sqrt(0.5 / n), effect_size=r, threshold=t,
  title=f"(correct) A/B test with size={n}, decision threshold = {t:.4f}",
  subtitle=f"1-power = {1-power:.2f}, significance = {significance:.2f}"))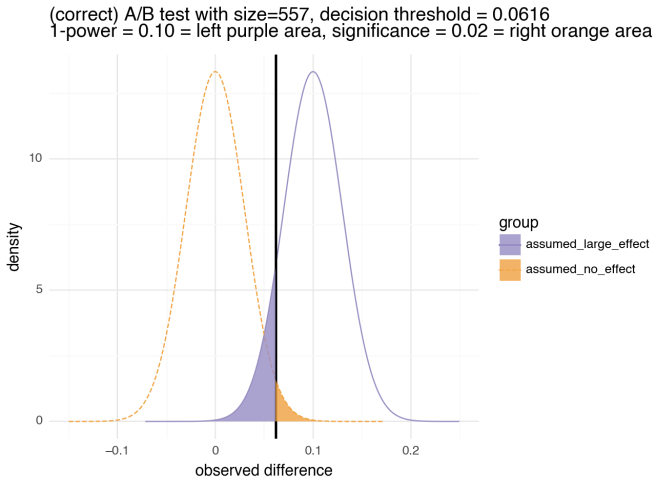

음영 처리된 영역의 면적은 다양한 실험 실패의 확률을 나타내므로 둘 다 작아야 합니다.

In practice again

실제 A/B 테스트 애플리케이션에서는 한 번만 실행하고 결과(및 실험 설계와 규칙)가 정확할 것이라는 수학적인 보증을 신뢰해야 합니다. 테스트를 한 번 실행해 봅시다.

# trying to detect if this is A or B from the returned result.
a_data = [a_completed() for i in range(n)]
b_data = [b_completed() for i in range(n)]
experiment_result = estimate_empirical_mean_difference(
    a_source=a_data, b_source=b_data)
think_B_is_much_better = experiment_result >= t

print(f"experiment_result: {experiment_result}")
print(f"Think B is much better: {think_B_is_much_better}.")

위의 결과가 0.062 이상이면 "B"가 훨씬 더 좋아 보인다고 말합니다. 다시 한 번, 임계값으로 0.1("Large Improvement"에 대한 의도된 정의)을 사용하지 않는다는 점에 유의하세요. 위의 모든 작업과 측정값을 의사 결정 임계값(Decision Threshold)을 사용하여 의사 결정으로 축소해야 합니다. 그 결과는 다음과 같습니다.

Out:
experiment_result: 0.10053859964093353
"Think B is much better: True."

Closing

처음부터 A/B 테스트의 간소화된 버전을 시연하면서 테스트의 주요 특징인 유의도(Significance)와 검정력(Power)에 익숙해질 수 있습니다. 또한 테스트 설계의 중요한 세부 사항인 '큰 차이'에 대한 사용자의 정의를 의사 결정 임계값으로 변환하는 방법에 대해서도 논의할 수 있습니다.
종종 A/B 테스트는 주어진 “B”가 큰지 아닌지를 확인하는 것이 아니라 큰 “B”를 찾으려고 하는 경우가 많습니다. “B”에 대한 주어진 영향(Effect Size)를 존중하거나 보호하려면 결정 임계값(Decision Threshold)을 이 영향값(Effect Size)보다 낮게 설정해야 합니다.

Appendices

Appendix: deriving the find n procedure

우리의 귀무 가설은 "B"가 "A"와 동일하다는 것입니다. 표본 크기가 n인 경우 위의 합계 차이의 확률 분포는 정규 분포에 매우 가까워집니다. 이는 "큰 수의 법칙" 때문입니다. 어떤 정규 분포를 사용할지는 실험의 평균과 분산에 의해 완전히 결정됩니다.
대부분의 통계 소프트웨어에는 관측값의 표준 편차가 몇 개인지 주어지면 해당(또는 더 극단적인) 이벤트가 얼마나 드문지를 알려주는 함수가 있습니다. 일반적으로 이러한 함수를 "역 누적 분포 함수(The Inverse Cumulative Distribution Function)"라고 하며, 주어진 확률 질량이 임계값의 왼쪽에 얼마나 위치하는지 알려줍니다. 파이썬에서 이 함수는 norm.ppf()입니다.
예를 들어 평균 0, 분산 1 정규 분포에서 그려진 숫자의 약 99%가 2.33을 넘지 않습니다. 이를 시연해 보겠습니다.

# draw a few examples of mean 0, variance 1 normally distributed numbers
print(rng.normal(size=5))

# show the threshold that about 99% of the draws we be no larger than
norm_99 = norm.ppf(0.99)
print(f"norm_99: {norm_99}")

# confirm the 99% rareness empirically.
m0 = np.mean(rng.normal(size=10000000) <= norm_99)
assert np.abs(m0 - 0.99) < 1e-3

print(f"m0: {m0}")

Out:
array([1.3628394 , 0.39827192, 0.08119358, 0.40168916, 1.20065715])
norm_99: 2.3263478740408408
m0: 0.9899827

norm.ppf()가 얼마나 복잡한지는 이미 구현되어 있기 때문에 중요하지 않습니다. 익숙해지면 그 다음 단계가 편해질 뿐입니다. 우리가 무언가를 증명하는 것이 아니라, 우리가 확립하고자 하는 것을 표준 결과로 간주되는 것과 연결시키는 것입니다.

처음 접하는 분들을 위해: 우리가 관심을 갖고 있는 것(그러나 믿지 않음)들을 우리가 아직 관심을 갖고 있지 않은 것(또한 아직 믿지 못할 수도 있음)들과 연관시키는 것처럼 느껴집니다. 사실 우리는 도메인별 또는 애플리케이션 지향적인 우리의 주장을 좀 더 근본적인 것으로 간주되는 주장과 연관시키려고 노력하고 있습니다. 즉, A/B 및 A/A 테스트 계획 코드에 들어갈 표현식을 도출해 보겠습니다.

A/A 테스트의 경우 적어도 (1-유의도(Significance)) 확률로 유사해 보이는 임계값을 원합니다(실제로 동일하다는 가정 하에). A/A 테스트에서 값이 유사하면 비슷한 판단을 내릴 확률도 올바른 판단을 내릴 확률이기 때문입니다. 이 "귀무 가설" 하에서 estimate_empirical_mean_difference()의 기대값은 0이고 분산은 sqrt((p1 (1-p1) + p2 (1-p2))/ n)입니다(이항 분포와 독립 분산의 가산성에서). 여기서 p1 = p2는 둘 다 동일한(알 수 없는) 성공률입니다. p를 알 수 없으므로 (p1 (1-p1) + p2 (1-p2))를 최대화하는 p = 1/2의 상한을 사용합니다.
우리가 기대하는 것:

  t = norm_cdf_inverse(1 - significance) * sqrt((p1 * (1-p1) + p2 * (1-p2)) / n)

위에서는 임계값 오른쪽의 값이 유의도(Significance)면 임계값 왼쪽은 (1 - 유의도(Significance))입니다. 위의 유의도(Significance) 요건을 충족하는 데 필요한 n에 대해 다음과 같이 이 문제를 해결할 수 있습니다(norm.ppf() 보다 method명이 직관적인 norm_cdf_inverse() 사용):

t, p1, p2, significance, n = \
sympy.symbols("t, p1, p2, significance, n", positive=True)

# solve f(n) = t for n
sympy.solve(
    norm_cdf_inverse(1 - significance) * \
    sympy.sqrt((p1 * (1-p1) + p2 * (1-p2)) / n) - t,
    n)

Out:
[norm_cdf_inverse(1 - significance)**2*(-p1**2 + p1 - p2**2 + p2)/t**2]

이 방정식은 A/B 테스트의 "big club"입니다. 이를 통해 다양한 조건을 충족하는 데 필요한 단계 수를 추정할 수 있습니다. 여기서 주목해야 할 매우 중요한 점은 n이 (1/t)2 만큼 선형적으로 증가한다는 것입니다. 이는 작은 (종종 가치가 없는) 차이를 테스트하는 데 매우 많은 비용이 든다는 것을 의미합니다.
분산 범위를 더 엄격하게 설정하거나, 소위 "연속성 보정(Continuity Correction)"(분포가 k/n 형식의 숫자만 반환한다는 사실을 이용)을 통해 추정치를 약간 강화하거나, 실제 이항 분포의 차이에 대해 정확한 누적 분포 함수를 사용하는 것도 가능합니다. 현재 상황에서는 그 어느 것도 중요하지 않습니다.

위의 해결책을 사용하여 method를 정의할 수 있습니다: find_n_for_given_mass_of_binomial_left_of_threshold(mass=1 - significance, threshold=t)은 유의성 목표를 충족하는 시도 횟수 n을 반환합니다. 비슷한 인수를 사용하면 주어진 검정력(Power)를 달성하는 데 필요한 n은 find_n_for_given_mass_of_binomial_left_of_threshold(mass=power, threshold=r - t)로 계산할 수 있습니다.

# solve f(n) = t for n
r, power = sympy.symbols("r power")
sympy.solve(
    norm_cdf_inverse(power) * sympy.sqrt((p1 * (1-p1) + p2 * (1-p2)) / n) - (r-t),
    n)

Out:
[norm_cdf_inverse(power)**2*(-p1**2 + p1 - p2**2 + p2)/(r - t)**2]

Appendix: deriving the threshold adjustment

우리가 주장하는 임계값 조정은 t = threshold_adjust * r 입니다.
두 기준 중 최악을 최소화하기 위한 파라미터를 선택할 때 가장 좋은 파라미터는 기준이 일치하는 곳입니다. 즉, 경계 기준 중 하나가 경계에서 더 멀리 떨어져 있으면 최대값에 영향을 주지 않고 다른 기준이 유리하도록 매개변수를 이동할 수 있습니다. 따라서 최적값에서는 양쪽 경계에 모두 닿게 됩니다. 이를 통해 최적의 threshold_adjust를 선택할 수 있습니다:

find_n_for_given_mass_of_binomial_left_of_threshold(
    mass=1-significance, threshold=t) = \
        find_n_for_given_mass_of_binomial_left_of_threshold(
            mass=power, threshold=r-t)
# set up our algebraic symbols.
mass, r, p1, p2, power, significance, threshold_adjust = sympy.symbols(
    "mass r p1 p2 power significance threshold_adjust", positive=True)

# solve for the required run times matching
sympy.solve(
    find_n_for_given_mass_of_binomial_left_of_threshold(
        mass=1-significance, threshold=threshold_adjust * r, p1=p1, p2=p2) \
        - find_n_for_given_mass_of_binomial_left_of_threshold(
              mass=power, threshold=r - threshold_adjust * r, p1=p1, p2=p2),
    threshold_adjust)

Out:

[norm_cdf_inverse(1 - significance) /
    (norm_cdf_inverse(1 - significance) - norm_cdf_inverse(power)),
 norm_cdf_inverse(1 - significance) / 
    (norm_cdf_inverse(1 - significance) + norm_cdf_inverse(power))]

제곱근(양수 또는 음수 부호를 가질 수 있음)을 취했기 때문에 두 가지 솔루션이 있습니다. 정답이 항상 양수라는 것을 알고 있으므로 항상 양수를 선택하고 함수 find_threshold_adjustment()를 도출했습니다.

위의 솔루션에서 임계값 조정은 지정된 검정력(Power)과 유의도(Significance)에만 의존하므로 주어진 요구 사항에 대해 상수로 취급할 수 있습니다. 또한 대칭 요구 사항 (1 - 검정력(Power) = 유의도(Significance))인 경우 threshold_adjust = 0.5가 됩니다. 이러한 대칭성은 기존의 "일반 효과 단위로 변환(Converted To Normal Effect Units)"이 아닌 "비율 효과 단위의 차이(Difference Of Rates Effect Units)"로 직접 작업할 때 얻을 수 있는 이점 중 하나입니다.

Appendix: picking significance and power goals

일반적으로 테스트는 r이 0에 가까워질수록 훨씬 더 어려워지고, 유의도(Significance)가 0에 가까워지고 검정력(Power)이 1에 가까워질수록 다소 어려워집니다. 이러한 금지된 값 근처에서 작동하는 테스트를 할 수 있지만 이는 실용적이지 않습니다. 따라서 사용자는 테스트 길이(비용과 대기 시간을 직접 제어)와 테스트 값(매개변수를 금지 값 근처로 설정)의 절충점을 지정합니다. 대략적으로 쓸모없는 "B"가 많을수록 0에 가까울수록 유의도(Significance)를 설정해야 합니다. "B" 효과를 내기 위한 변경 사항을 개발하는 데는 1에 가까울수록 더 많은 비용이 듭니다. 또한 큰 개선 사항을 찾기가 더 어렵고, r을 0에 가깝게 설정할수록 더 큰 규모의 개선 사항을 사용할 수 있습니다. 일반적인 기본값인 0.8은 잘 설명되지 않은 잘못된 선택입니다. 일반적인 기본값인 유의도(Significance) = 0.05는 특별한 것이 아니며, 테스트 신뢰도를 높이기 위해 더 낮은 값으로 낮추는 것이 일반적입니다.

Appendix: the threshold for “the usual test”

일반적인 A/B 테스트는 (특별한 이유 없이) 5%의 유의도(Significance)와 80%의 검정력(Power)를 선택합니다. 이러한 설정에 대한 임계값 조정을 살펴보겠습니다.

find_threshold_adjustment(significance=0.05, power=0.8)

Out:
0.6615203125780165

이는 확인하려는 비율 값에 대한 결정 임계값을 약 66%로 설정하여 테스트를 실행하는 적절한 방법임을 나타냅니다. 사실 이것은 매우 간단한 규칙입니다.

Appendix: solutions code

위의 수학적 도출이 완료되었으므로 코드를 표시할 준비가 되었습니다.

from scipy.stats import norm
import sympy

def norm_cdf_inverse(mass):
    """
    Inverse of normal cumulative distribution function.
    :param mass: probability mass
    :return: t such that P[x <= t] = mass \
            for the mean 0 standard deviation 1 normal distribution
    """
    if isinstance(mass, sympy.Expr):
        # return a new symbol, if working symbolically
        return sympy.Symbol(f"norm_cdf_inverse({mass})", positive=True)
    return norm.ppf(float(mass))

def find_n_for_given_mass_of_binomial_left_of_threshold(
        *, mass, threshold, p1 = 0.5, p2 = 0.5):
    """
    Find n so that no more than a mass fraction of 
    Binomial(count=n, prob=0.5)/n - Binomial(count=n, prob=0.5)/n 
    is at or above threshold.
    This is from an approximation of this as normal with mean 0 
    and variance ((p1 * (1 - p1)) + (p2 * (1 - p2)) / n. 
    :param mass: probability we say difference of means should be
                 no more than threshold.
    :param threshold: our point of comparison for observed difference in means.
    :param p1: assumed p1 probability bound 
               (used for variance bound, can use 0.5 for upper bound).
    :param p2: assumed p2 probability bound
               (used for variance bound, can use 0.5 for upper bound).
    :return: n 
    """
    return 
        ((norm_cdf_inverse(mass) / threshold)**2 *
         ((p1 * (1 - p1)) + (p2 * (1 - p2))))

def find_threshold_adjustment(*, power, significance):
    """
    get the threshold adjustment, find "a" such that:
    find_n_for_given_mass_of_binomial_left_of_threshold(
        mass=1-significance, threshold=a * r, p1, p2) = \
            find_n_for_given_mass_of_binomial_left_of_threshold(
                mass=power, threshold=r - a * r, p1, p2)
    where r is the proposed change in rates effect size.
    :param power: proposed true positive rate
    :param significance: proposed false positive rate
    :return: threshold_adjustment "a" s.t. threshold = a * r
    """
    return 1 / (1 + norm_cdf_inverse(power) / norm_cdf_inverse(1 - significance))