3D Point Cloud 에 대해 모델링하면서 3D를 2D로 projection 또는 2D영상을 3D로 표현함에 있어 필요로 되는 지식들을 공부하고자 이 글을 작성하게 되었다.
먼저 Geometry의 기본이 되는 내용인 영상 좌표계 (Image Coordinate System)에 대해 설명할 것이다.
아주 기초적인 내용을 다루고 있고, 다른 블로그에서도 이와 같은 내용을 많이 다루고 있기 때문에 본 내용은 다른 글을 참고해도 좋다.
1. 좌표계 (Coordinate system)
영상 좌표계에는 크게 총 4가지의 좌표계가 존재하는데, 월드 좌표계, 카메라 좌표계, 정규 좌표계, 픽셀 좌표계가 있다.
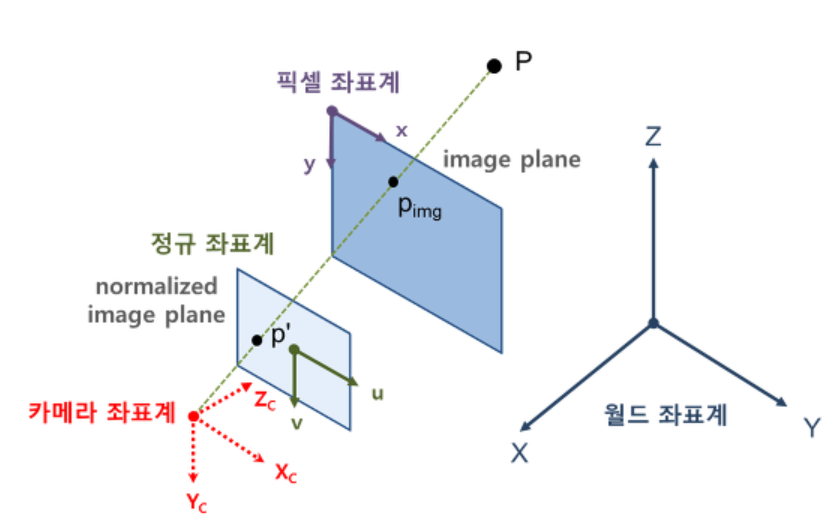
1.1. 월드 좌표계 (World Coordinate System)
월드 좌표계는 사물의 위치를 표현하기 위해 임의로 원점(0,0,0 ; 기준)으로 한 좌표계이다.
예를 들어서, 방의 한쪽 모서리가 원점이라면 한쪽 벽면 방향이 X축, 다른쪽 벽면 방향이 Y축, 천장 모서리가 Z축으로 할 수 있다.
(월드 좌표계의 한점을 표현하기 위해 좌표를 대문자 X, Y, Z로 표기하였다.)
1-2. 카메라 좌표계 (Camera Coordinate System)
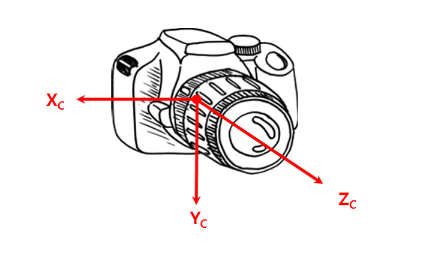
카메라 좌표계는 카메라 초점(렌즈의 중심)을 원점(0,0,0; 기준)으로 한 좌표계이다.
카메라의 정면방향을 Z축, 카메라의 아래방향을 Y축, 오른쪽 방향을 X축으로 설정하여 사용할 수 있다.
(카메라 좌표계의 한점을 표현하기 위해 대문자에 아래첨자 c를 붙여서 Xc, Yc, Zc로 표기하였다.)
1-3. 픽셀 좌표계 (Pixel Coordinate System)

픽셀 좌표계는 다른 말로 이미지 좌표계이다. 따라서 Image Coordinate System이라고도 한다.
이미지의 left-top 모서리를 원점(0,0,0), 오른쪽 방향을 X축 증가방향, 아래쪽 방향을 Y축 증가방향으로 한다 .
픽셀 좌표계의 X축, Y축에 의해 결정되는 평면을 Image plane (이미지 평면)이라고 한다.
3D 공간상의 한 점 P = (X, Y, Z)는 카메라의 초점을 지나서 이미지 평면의 한 점 Pimg = (x,y)에 투영(projection)된다. 점 P와 점Pimg를 잇는 선(ray) 상에 있는 모든 3D 점들은 모두 Pimg로 투영된다.
따라서 3D 좌표상의 한 점 P로부터 2d 좌표상의 한 점 Pimg는 유일하게 한 점으로 결정되지만, Pimg로 부터 P를 구하는 것은 부가적인 정보없이는 불가능하다.
1-4. 정규 좌표계 (Normalized Image Coordinate System)
지금까지 설명한 좌표계는 모두 직관적인 좌표계이지만 정규 좌표계는 편의상 도입된 가상의 좌표계이다.
다른 말로 설명하면,
1. 카메라의 내부 파라미터(intrinsic parameter)의 영향을 제거한 이미지 좌표계.
2. 좌표계의 단위를 없앤(정규화된) 좌표계
3. 이미지 평면을 평행이동시켜서 카메라 초점과의 거리가 1인 지점으로 옮겨놓은 이미지 평면 좌표계
정규 좌표계의 원점은 정규 이미지 평면의 중점(광학축 Zc와의 교점)이다.
따라서 좀 더 생각하자면, 원래의 이미지 평면을 평행이동시켜서 카메라 초점과의 거리가 1인 지점으로 옮겨놓은 이미지 평면이라고 볼 수 있다.
"카메라 내부 파라미터"를 알면 다음과 같이 픽셀 좌표와 정규 좌표 사이의 변환이 가능하다.
(카메라의 내부 파라미터에 대한 내용은 다음 글에서 기술하겠다.)
정규 이미지 평면과 정규 좌표계를 도입한 이유는 카메라 간의 차이(동일한 장면을 동일한 위치와 동일한 각도에서 찍더라도 사용한 카메라에 따라, 세팅에 따라 얻는 차이)을 제거하기 위해서이다. 이와 같은 요소는 일관된 기하학적 해석을 하는 데 불필요한 요소일 것이기 때문이다.